Kapitel
Betrachtet man eine Gerade 
und eine Ebene 
im Raum, so sind diese auf eine der folgenden drei Arten positioniert:
1 ist in enthalten.
2 und sind parallel.
3 und sind Sekanten.
Je nach Ausdruck der Geraden gibt es folgende Fälle:
Die Gerade wird durch zwei sich schneidende Ebenen definiert
Wir sehen uns die Gerade an, die durch zwei sich schneidende Ebenen definida por dos planos secantes 
und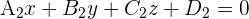 
definiert ist
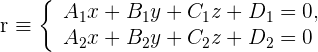
und die Ebene 
.
Um die Lagebeziehung der Geraden und der Ebene zu untersuchen, betrachten wir das System:
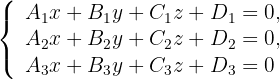
Wir bezeichnen mit 
den Rang der Koeffizientenmatrix und mit 
den Rang der erweiterten Matrix. Die Lagebeziehungen der Geraden und der Ebene sind in der folgenden Tabelle angegeben:
| Lage | | |
|---|---|---|
| Gerade in der Ebene enthalten | 2 | 2 |
| Gerade und Ebene parallel | 2 | 3 |
| Gerade und Ebene Sekanten | 3 | 3 |
Gerade durch einen Punkt und einen Vektor definiert
Wenn die Gerade durch den Punkt 
und den Richtungsvektor 
definiert ist und die Ebene den Normalenvektor 
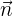hat. Die Lagebeziehungen der Geraden und der Ebene sind:
Gerade in der Ebene enthalten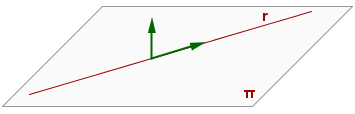
Gerade und Ebene parallel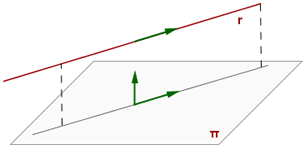
Gerade und Ebene Sekanten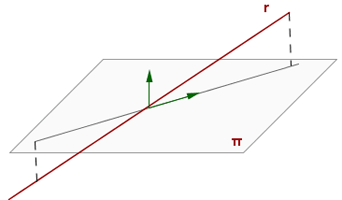
Die relativen Lagebeziehungen der Geraden und der Ebene lassen sich durch Untersuchung der Position des Punktes auf der Geraden und des Skalarprodukts des Richtungsvektors der Geraden und des Normalenvektors der Ebene berechnen
| Lage |  | |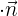
|---|---|---|
| Gerade in der Ebene enthalten |  |  |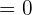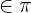
| Gerade und Ebene parallel | |  |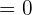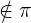
| Gerade und Ebene Sekanten |  |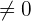
Aufgaben
Ermittle die relative Lage der Geraden und der Ebene:
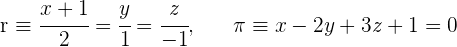
1Zunächst wandeln wir die stetigen Gleichungen in implizite Gleichungen um
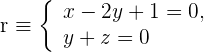
2Wir diskutieren das System, das aus der Geraden und der Ebene besteht.
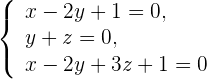
3Wir schreiben die Koeffizientenmatrix
4Wir berechnen die Determinante
Der Rang ist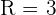 
5Wir berechnen den Rang der erweiterten Matrix
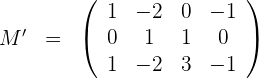
Dieser ist 
und es genügt, wenn wir uns die Matrix 
ansehen.
6Da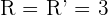 
, sind die Gerade und Ebene Sekanten.
Ermittle die relative Lage der Geraden und der Ebene:
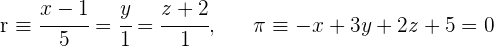
1Anhand der stetigen Gleichungen der Geraden erhalten wir den Punkt und den Richtungsvektor . Dabei beachten wir, dass
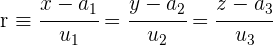
und schließlich 
und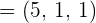 
2Der Normalenvektor der Ebene wird durch die Koeffizienten gebildet. Somit 
3Wir berechnen das interne Produkt des Richungsvektors und des Normalenvektors
4Wir überprüfen, ob sich in der Ebene befindet. Hierzu setzen wir den Punkt in die Gleichung der Ebene ein
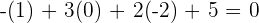
Da die Gleichung der Ebene erfüllt ist, haben wir 
5Aus der zweiten Tabelle schließen wir, dass die Gerade in der Ebene enthalten ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
