Der Schnittwinkel zweier Geraden entsteht, wenn zwei Geraden sich schneiden.
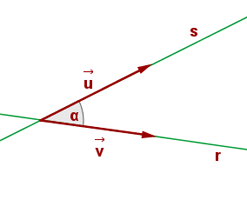
Diesen erhalten wir durch:
1 Die Richtungsvektoren.
Betrachten wir die Vektoren 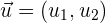 und
und 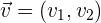 als Richtungsvektoren der Geraden
als Richtungsvektoren der Geraden 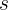 und
und  , so ist der Kosinus des von den Geraden gebildeten Winkels:
, so ist der Kosinus des von den Geraden gebildeten Winkels:
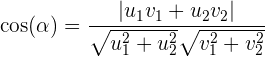
2Die Steigungen der Geraden.
Wenn 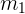 die Steigung der Geraden
die Steigung der Geraden  und
und 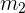 die Steigung der Geraden
die Steigung der Geraden 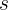 ist, können wir mit der folgenden Formel den Tangens des Winkels zwischen den Geraden und damit den Winkel ermitteln:
ist, können wir mit der folgenden Formel den Tangens des Winkels zwischen den Geraden und damit den Winkel ermitteln:

Wenn 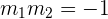 , bedeutet dies, dass die beiden Geraden senkrecht zueinander sind und
, bedeutet dies, dass die beiden Geraden senkrecht zueinander sind und 
Beispiele
1 Berechne den Winkel, den die Geraden 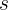 und
und  bilden.
bilden.
Wir wissen, dass die Richtungsvektoren wie folgt lauten:: 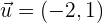 und
und 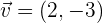 .
.
Zunächst berechnen wir den Kosinus des Winkels:
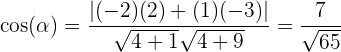
Nun können wir den gesuchten Winkel berechnen
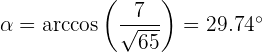
2 Gegeben sind die Geraden 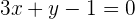 und
und 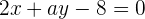 .
.
Bestimme  , sodass sie einen Winkel von
, sodass sie einen Winkel von  bilden.
bilden.
Wenn wir eine Bezugsgerade haben und eine andere Gerade finden sollen, die bei  liegt, bedeutet dies, dass wir nach zwei möglichen Geraden suchen, da die Grade sich sowohl im als auch gegen den Uhrzeigersinn bilden können. Wir analysieren also zwei Fälle:
liegt, bedeutet dies, dass wir nach zwei möglichen Geraden suchen, da die Grade sich sowohl im als auch gegen den Uhrzeigersinn bilden können. Wir analysieren also zwei Fälle: 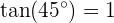 und
und 
Zunächst bringen wir jede der Geraden in folgende Form:
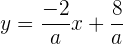 bedeutet, dass
bedeutet, dass 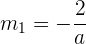
 bedeutet, dass
bedeutet, dass 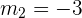
Da wir nun beide Steigungen haben, erstellen wir die erste Gleichung basierend auf
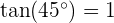
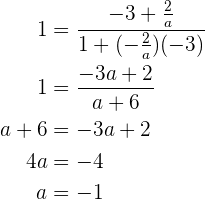
So erhalten wir unseren ersten Wert 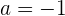
Betrachten wir nun den Fall, dass 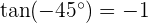
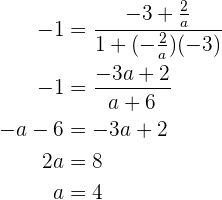
So erhalten wir unseren zweiten Wert 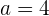
Mit KI zusammenfassen:



