
Parallele Geraden
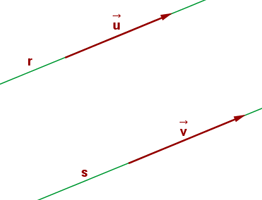
Sieh dir folgende Abbildung mit 2 parallelen Geraden an. Wenn die Geraden  und
und  parallel sind, schreiben wir
parallel sind, schreiben wir 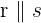 .
.
Anhand des Richtungsvektors: Zwei Geraden sind parallel, wenn der Richtungsvektor einer der Geraden der Richtungsvektor der zweiten Geraden, multipliziert mit einer Zahl 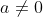
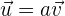
Wenn also  und
und  , sind die Geraden parallel, wenn
, sind die Geraden parallel, wenn
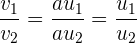
Auf diese Weise kann man mit den Richtungsvektoren herausfinden, ob zwei Geraden parallel sind.
Anhand der Steigung der Geraden: Zwei Geraden sind parallel, wenn ihre Steigung gleich ist. Das heißt:
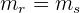
Da die Steigung einer Geraden 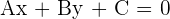 mittels
mittels 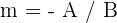 berechnet wird, sind zwei Geraden
berechnet wird, sind zwei Geraden
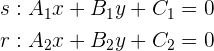
parallel, wenn gilt:
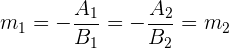
Und somit
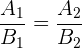
So kann man anhand der allgemeinen Gleichung zweier Geraden feststellen, ob sie parallel sind.
Zueinander senkrechte Geraden
Sieh dir nun folgende zueinander senkrechte Geraden an. Die zueinander senkrechten Geraden bilden einen  -Winkel. Wenn also
-Winkel. Wenn also  und
und  zueinander senkrecht sind, schreiben wir
zueinander senkrecht sind, schreiben wir  .
.
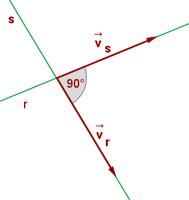
Anhand der Richtungsvektoren: Zwei Geraden sind zueinander senkrecht, wenn ihre Richtungsvektoren zueinander senkrecht sind:

Dies stellt das Skalarprodukt aus  und
und 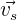 dar.
dar.
Anhand der Steigung der Geraden: Wenn zwei Geraden zueinander senkrecht sind, entspricht das Produkt ihrer Steigungen a 
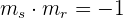
Dies ist äquivalent zu:
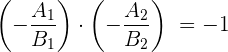
Das heißt
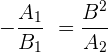
So kann man bestimmen, ob zwei Geraden zueinander senkrecht sind.
Aufgaben zu parallelen und senkrechten Geraden
1 Bestimme eine parallele Gerade und eine andere Gerade senkrecht zu  , die durch den Punkt
, die durch den Punkt  verlaufen.
verlaufen.
Lösung: Zunächst bestimmen wir die parallele Gerade  . Es muss gelten
. Es muss gelten
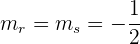
Somit ist die Gleichung in Punktsteigungsform von  gegeben durch
gegeben durch
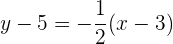
Wir wandeln die Gleichung in die Normalform um
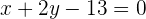
Nun suchen wir die senkrechte Gerade  . In diesem Fall müssen wir Folgendes beachten:
. In diesem Fall müssen wir Folgendes beachten:
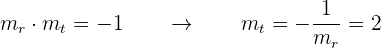
Somit ist die Gleichung in Punktsteigungsform von  gegeben durch
gegeben durch
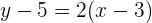
Wir stellen die Gleichung um und erhalten
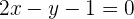
2 Berechne den Wert für  , sodass die Geraden
, sodass die Geraden  und
und 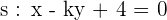 parallell sind. Berechne außerdem den Wert für
parallell sind. Berechne außerdem den Wert für  , sodass die Geraden zueinander senkrecht sind.
, sodass die Geraden zueinander senkrecht sind.
Lösung: Die Gleichungen haben folgende Steigungen
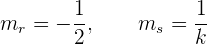
Wenn wir also möchten, dass die Geraden parallel sind, muss gelten

Wir erhalten
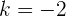
Und wenn wir möchten, dass die Geraden zueinander senkrecht sind, muss gelten
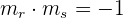
Das heißt

Wir erhalten
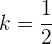
Mit KI zusammenfassen:













