Kapitel
In diesem Abschnitt befassen wir uns mit dem Umkreismittelpunkt eines Dreiecks. Außerdem erfahren wir, wie man die Mittelsenkrechte eines Dreiecks und den Flächeninhalt des durch die Eckpunkte eines Dreiecks verlaufenden Kreises berechnet.

Mittelsenkrechte und Umkreismittelpunkt eines Dreiecks
Im weiteren Verlauf zeigen wir dir die Definitionen des Umkreismittelpunkts und der Mittelsenkrechten.
Die Mittelsenkrechten eines Dreiecks sind die senkrechten Geraden, die durch die Mittelpunkte der Seiten des Dreiecks verlaufen.
Der Umkreismittelpunkt ist der Schnittpunkt der drei Mittelsenkrechten.
Der Umkreismittelpunkt wird mit dem Buchstaben  dargestellt.
dargestellt.
Der Umkreismittelpunkt ist der Mittelpunkt des Umkreises eines Dreiecks.
Mittelsenkrechte und Umkreismittelpunkt eines Dreiecks
Nun sehen wir uns die Definitionen des Umkreismittelpunkt und der Mittelsenkrechte an.
Die Mittelsenkrechten eines Dreiecks sind die senkrechten Geraden, die durch die Mittelpunkte der Seiten des Dreiecks verlaufen.
Der Umkreismittelpunkt ist der Schnittpunkt der drei Mittelsenkrechten.
Der Umkreismittelpunkt wird mit dem Buchstaben  dargestellt.
dargestellt.
Der Umkreismittelpunkt ist der Mittelpunkt des Umkreises eines Dreiecks.
Aufgabe
Ermittle die Gleichungen der Mittelsenkrechten und den Umkreismittelpunkt des Dreiecks mit den Eckpunkten:  und
und 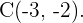
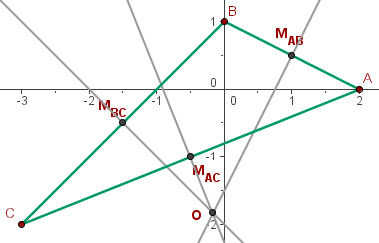
Schritt 1: Gleichung der Mittelsenkrechte, die durch den Mittelpunkt von  verläuft.
verläuft.
Als Erstes bestimmen wir den Mittelpunkt von  . Dazu müssen wir nur die Koordinaten der Punkte
. Dazu müssen wir nur die Koordinaten der Punkte  und
und  subtrahieren und dann durch
subtrahieren und dann durch  dividieren. Das heißt,
dividieren. Das heißt, 
Als Nächstes müssen wir die Steigung der Senkrechten zur Seite  ermitteln. Da die Steigung der Geraden, die durch die Punkte
ermitteln. Da die Steigung der Geraden, die durch die Punkte  und
und  verläuft,
verläuft, 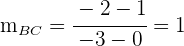 ist,
ist,
und das Produkt der Steigungen einer Geraden und ihrer Senkrechten -1 ist, ist die Steigung unserer Mittelsenkrechte 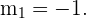
Schließlich wenden wir die Punkt-Steigungs-Form an und erhalten die Gleichung der Mittelsenkrechte: 
Schritt 2: Gleichung der Mittelsenkrechten, die durch den Mittelpunkt von  verläuft.
verläuft.
Wir gehen in ähnlicher Weise vor wie im vorherigen Schritt. Zunächst ermitteln wir den Mittelpunkt von  . Dazu müssen wir nur die Koordinaten der Punkte
. Dazu müssen wir nur die Koordinaten der Punkte  und
und  subtrahieren und dann durch
subtrahieren und dann durch  dividieren. Das heißt,
dividieren. Das heißt, 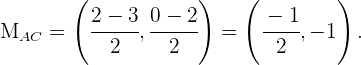
Als Nächstes bestimmen wir die Steigung der Senkrechten auf die Seite  . Da die Steigung der Geraden, die durch die Punkte
. Da die Steigung der Geraden, die durch die Punkte  und
und  verläuft,
verläuft,
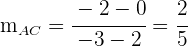 ist,
ist,
und das Produkt der Steigungen einer Geraden und ihrer Senkrechten -1 ist, ist die Steigung unserer Mittelsenkrechte 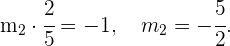
Schließlich wenden wir die Punkt-Steigungs-Form an und erhalten die Gleichung der Mittelsenkrechte zur Strecke  :
: 
Schritt 3: Gleichung der Mittelsenkrechte, die durch den Mittelpunkt von  verläuft.
verläuft.
Wir gehen in ähnlicher Weise vor wie im vorherigen Schritt. Zunächst ermitteln wir den Mittelpunkt von  . Dazu müssen wir nur die Koordinaten der Punkte
. Dazu müssen wir nur die Koordinaten der Punkte  und
und  subtrahieren und dann durch
subtrahieren und dann durch  dividieren. Das heißt,
dividieren. Das heißt, 
Als Nächstes bestimmen wir die Steigung der Senkrechten auf die Seite  . Da die Steigung der Geraden, die durch die Punkte
. Da die Steigung der Geraden, die durch die Punkte  und
und  verläuft,
verläuft,
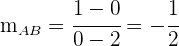 ist,
ist,
und das Produkt der Steigungen einer Geraden und ihrer Senkrechten -1 ist, ist die Steigung unserer neuen Mittelsenkrechte 
Schließlich wenden wir die Punkt-Steigungs-Form an und erhalten die Gleichung der Mittelsenkrechte zur Strecke  :
: 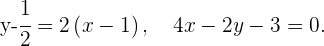
Schritt 4: Ermittle den Umkreismittelpunkt.
Der Umkreismittelpunkt ist der Schnittpunkt der drei Mittelsenkrechten. Um ihn zu berechnen, müssen wir das aus zwei Gleichungen bestehende System lösen.
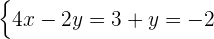
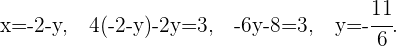

Der Umkreismittelpunkt ist
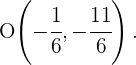
Fläche des Umkreises
Der Umkreismittelpunkt ist der Mittelpunkt des Umkreises, der durch die drei Eckpunkte des Dreiecks verläuft.
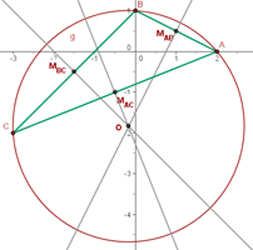
Für das obige Beispiel müssen wir die Fläche des Umkreises ermitteln. Der Radius des Umkreises ist die Distanz zwischen zwei Punkten: des Umkreismittelpunkts und eines Eckpunkts des Dreiecks. In diesem Fall nehmen wir den Punkt 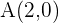 und den Umkreismittelpunkt
und den Umkreismittelpunkt 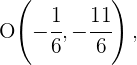
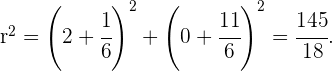
Da die Fläche eines Kreises gleich  mal Radius zum Quadrat entspricht, ist die Fläche unseres Umkreises
mal Radius zum Quadrat entspricht, ist die Fläche unseres Umkreises 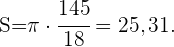
Mit KI zusammenfassen:












