Definition des Normalenvektors
Ein Normalenvektor zu einer Ebene ist ein Vektor, der senkrecht zu dieser Ebene steht. Daher steht jeder in der Ebene enthaltene Vektor senkrecht zum Normalenvektor.
Wenn 
den Normalenvektor einer Ebene 
darstellt und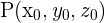 
ein Punkt der Ebene ist, kann die Gleichung der Ebene bestimmt werden.
Wir nehmen einen beliebigen Punkt 
der Ebene und konstruieren den Vektor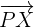 
, der sich in der Ebene befindet
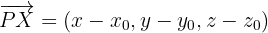
Da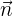 
ein Normalenvektor ist, steht er senkrecht zu 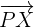und für beide gilt
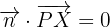
Mit dieser Gleichung können wir die allgemeine Ebenengleichung anhand eines Punktes und eines Normalenvektors bestimmen.
Aufgaben mit Vektoren
Ermittle die Gleichung der Ebene , die durch den Punkt 
verläuft und senkrecht zur Geraden 
steht.
1Da die Ebene senkrecht zu der Geraden steht, ist der Richtungsvektor der Geraden ein Normalenvektor der Ebene
2Wir berechnen den Richtungsvektor der Geraden . Diesen erhalten wir anhand der Koeffizienten des Parameters 
3Der Punkt 
der Ebene ist bekannt. Wir nehmen einen beliebigen Punkt 
und konstruieren einen Vektor der Ebene
4Wir berechnen das innere Produkt des Vektors in der Ebene und des Normalenvektors und setzen es gleich 0
Somit ist 
die Gleichung der Ebene
Ermittle die Gleichung der Geraden 
, die durch den Punkt 
verläuft und senkrecht zur Ebene 
steht.
1Die gesuchte Gerade steht senkrecht zur Ebene, daher ist der Normalenvektor zur Ebene ihr Richtungsvektor
2Der Normalenvektor wird aus den Koeffizienten 
der Gleichung der Ebene berechnet
3Der Punkt 
, durch den die Gerade verläuft, ist bekannt. Die Gleichung der Geraden, die durch den Punkt 
verläuft und den Richtungsvektor 
hat, ist gegeben durch
4Wir setzen die Werte des Punktes und des Richtungsvektors ein, um die Gleichung der Geraden zu erhalten
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
