Um den Abstand von einem Punkt P zu einer Geraden r herauszufinden, fällt man das Lot (d.h. man bildet eine Senkrechte zur Geraden, die durch den Punkt P verläuft) und misst dann die Länge des Abschnitts vom Punkt P zur Geraden.
Abstand Punkt-Gerade
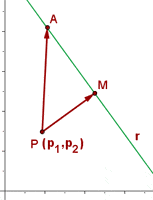
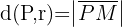
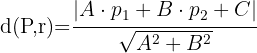
Beispiel
Bestimme den Abstand des Punktes 
zur Geraden 
der Gleichung 
.
Abstand Koordinatenursprung-Gerade
Beispiel
Bestimme den Abstand der Geraden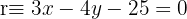 
zum Koordinatenursprung
.
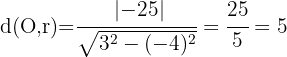
Abstand Gerade-Gerade
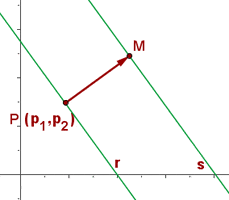
Um den Abstand zwischen zwei parallel verlaufenden Geraden zu bestimmen, wählt man einen beliebigen Punkt 
auf einer der Geraden aus und bestimmt dessen Abstand zur anderen Geraden.
Beispiel
1 Bestimme den Abstand zwischen der Geraden 
und 
.
Ermittle zuerst die Steigung der beiden Geraden, um sicher zu sein, dass sie parallel zueinander verlaufen
Finde einen Punkt auf einer der Geraden, um den Abstand zu ermitteln
Setze den Punkt in die Formel zur Bestimmung des Abstands eines Punkts zu einer Geraden ein
2 Bestimme nun den Abstand zwischen den beiden Geraden:
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
