Kapitel
Die Winkelhalbierenden eines Dreiecks sind die Geraden, die jeden Winkel des Dreiecks in zwei gleiche Winkel teilen.

Inkreismittelpunkt eines Dreiecks
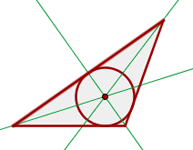
- Der Inkreismittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden.
- Der Inkreismittelpunkt wird mit dem Buchstaben
 angegeben.
angegeben. - Der Inkreismittelpunkt ist der Mittelpunkt eines in das Dreieck eingeschriebenen Kreises.
Übung zur Berechnung der Gleichungen der Winkelhalbierenden und der Inkreismittelpunkte
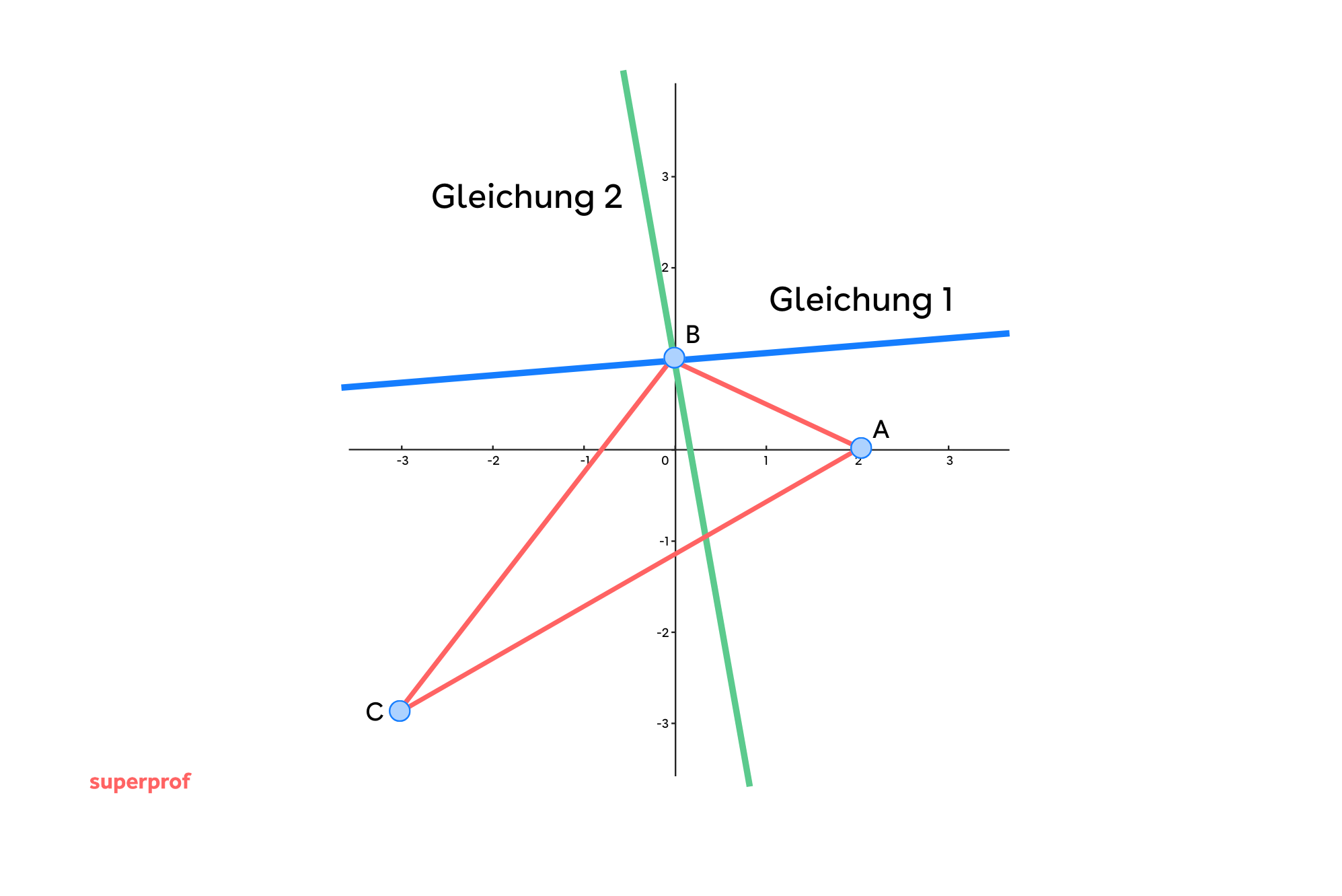
Ermittle die Gleichungen der Winkelhalbierenden und des Inkreismittelpunktes des Dreiecks mit den Eckpunkten:  und
und 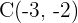 .
.
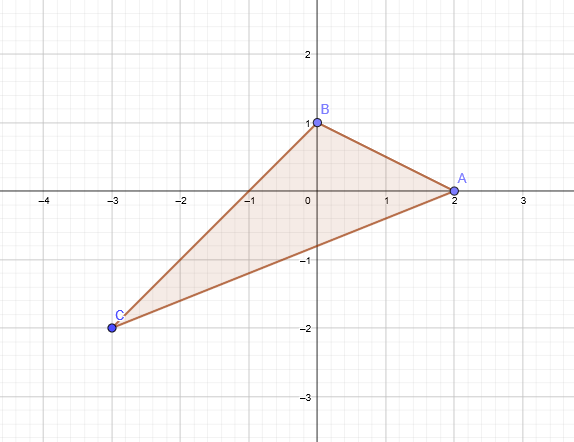
Zunächst finden wir die Gleichungen der Seiten des Dreiecks: Dazu verwenden wir die Punkt-Steigungsform der Geraden.
Gerade, die durch 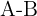 gebildet wird:
gebildet wird:
Wir berechnen die Steigung der Geraden, die durch die Punkte  und
und  gebildet wird
gebildet wird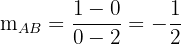
mit dieser Steigung und dem Punkt  erhalten wir die Gleichung der Geraden:
erhalten wir die Gleichung der Geraden: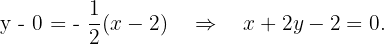
Gerade, die durch 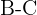 gebildet wird:
gebildet wird:
Gerade, die durch die Punkte 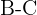 gebildet wird
gebildet wird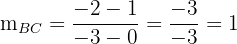
mit der Steigung und dem Punkt  erhalten wir die Gerade
erhalten wir die Gerade
Gerade, die durch 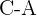 gebildet wird:
gebildet wird:
Die Steigung der Geraden, die durch die Punkte  und
und  gebildet wird, ist
gebildet wird, ist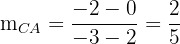
mit der Steigung und dem Punkt  erhalten wir die Gleichung der Geraden:
erhalten wir die Gleichung der Geraden: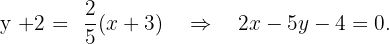
Berechnung der Winkelhalbierenden durch A.
Um die Gleichung der Winkelhalbierenden durch  zu ermitteln, nehmen wir die beiden Geraden, die den Winkel
zu ermitteln, nehmen wir die beiden Geraden, die den Winkel 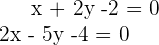 bilden
bilden
sowie 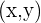 einen Punkt auf der Winkelhalbierenden. Da wir wollen, dass der Abstand zwischen dem Punkt und den Geraden in beiden Fällen derselbe ist, muss
einen Punkt auf der Winkelhalbierenden. Da wir wollen, dass der Abstand zwischen dem Punkt und den Geraden in beiden Fällen derselbe ist, muss
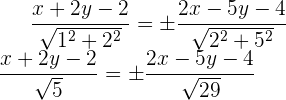 .
.
Das heißt, wir haben zwei Gleichungen (eine mit positivem und eine mit negativem Vorzeichen).
Erste Gleichung:
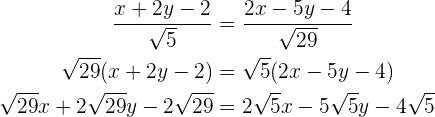
somit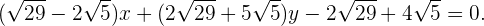
Wenn du nicht mit Wurzeln rechnen möchtest, könntest du eine Näherung mit Dezimalzahlen schreiben:
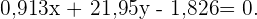
Zweite Gleichung:
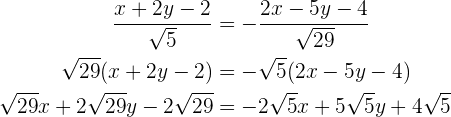
somit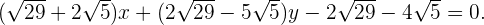
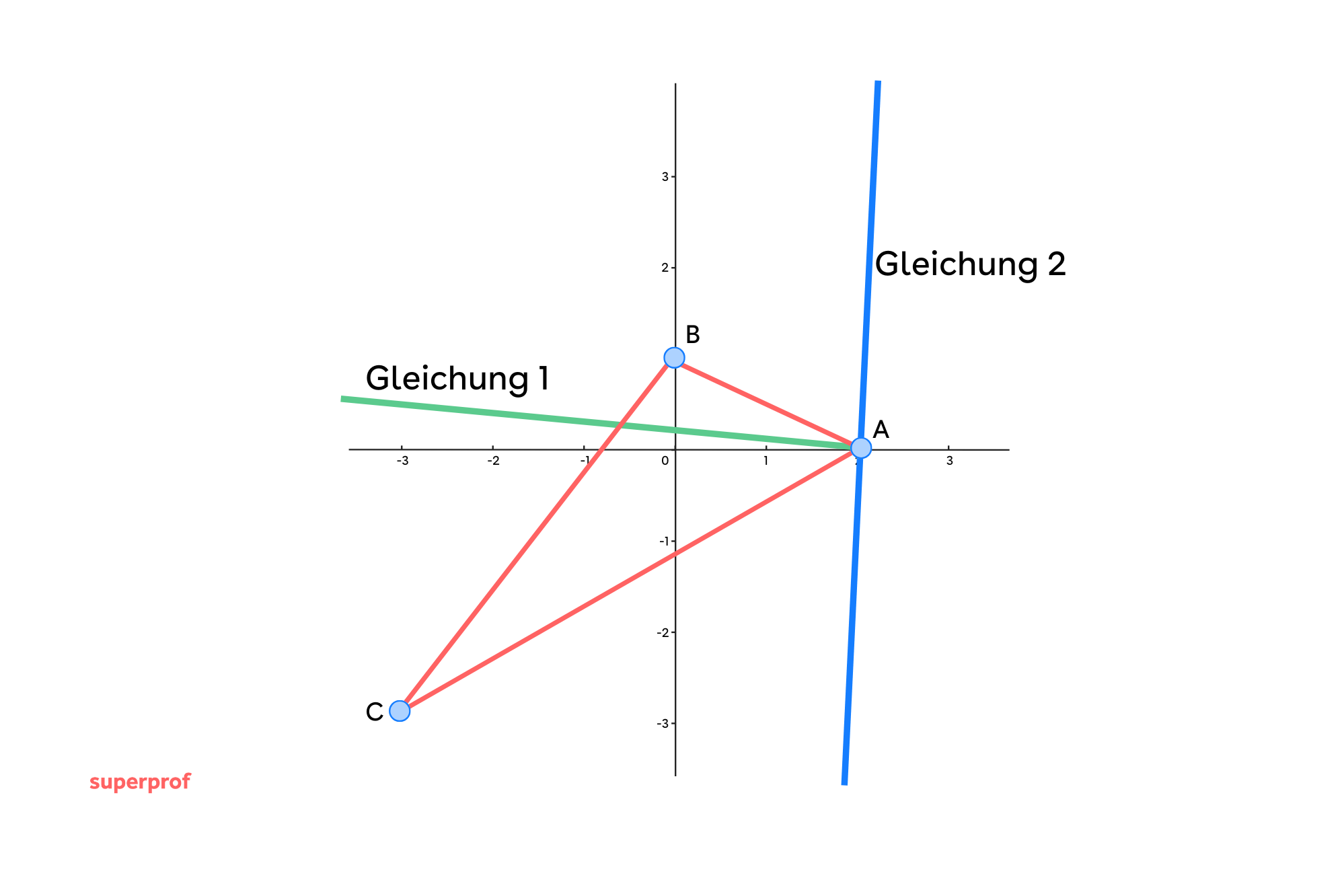
Mit Dezimalzahlen ausgedrückt: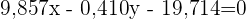
Berechnung der Winkelhalbierenden durch B.
In diesem Fall nehmen wir die Gleichung der zwei Geraden, die durch  verlaufen
verlaufen
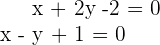
sowie 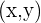 einen Punkt auf der Winkelhalbierenden. In diesem Fall:
einen Punkt auf der Winkelhalbierenden. In diesem Fall:
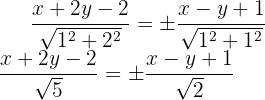
Erste Gleichung:
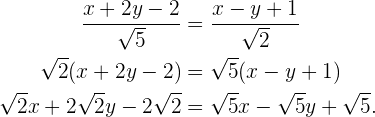
Somit
Mit Dezimalzahlen ausgedrückt: 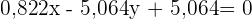
Zweite Gleichung:
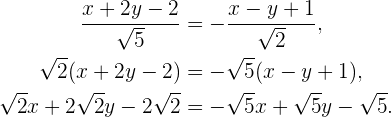
Somit
Mit Dezimalzahlen ausgedrückt: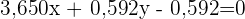
Berechnung der Winkelhalbierenden durch C.
Um die Gleichung der Winkelhalbierenden durch  zu ermitteln, nehmen wir die beiden Geraden, die den Winkell bilden
zu ermitteln, nehmen wir die beiden Geraden, die den Winkell bilden
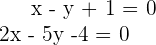
sowie 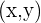 sowie einen Punkt auf der Winkelhalbierenden. Somit
sowie einen Punkt auf der Winkelhalbierenden. Somit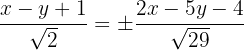
und die beiden Gleichungen
Erste Gleichung:
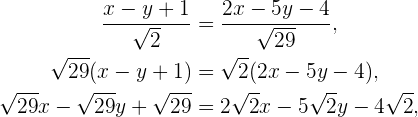
somit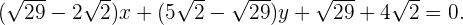
Mit Dezimalzahlen ausgedrückt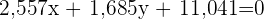
Zweite Gleichung:
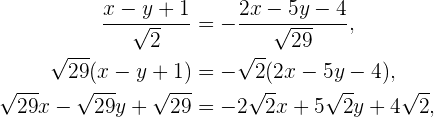
somit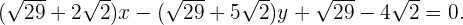
Wir schreiben in Dezimalform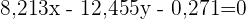
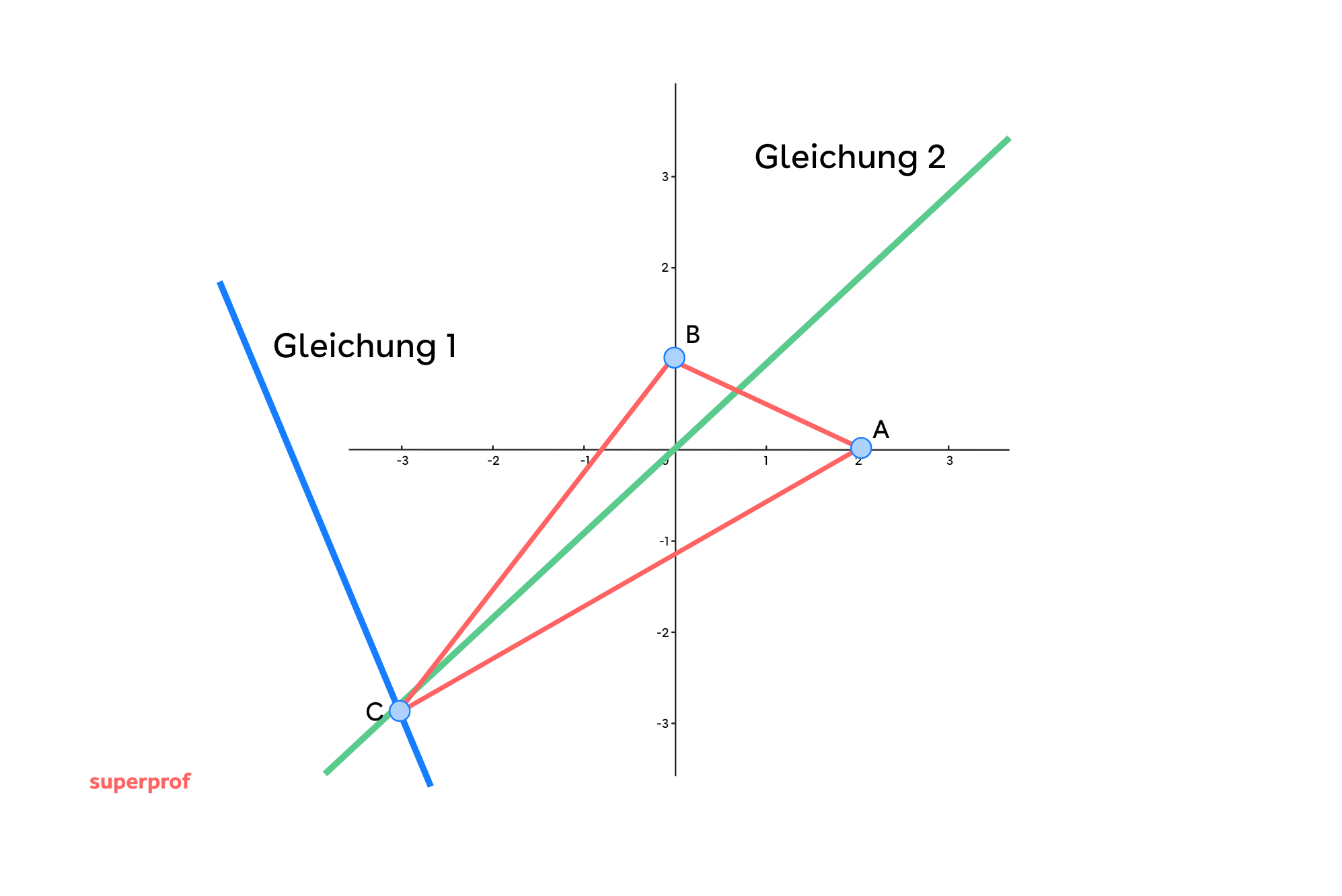
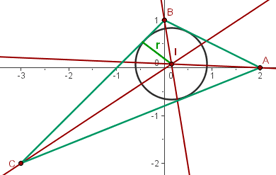
Berechnung des Inkreismittelpunkts
Der Inkreismittelpunkt ist der Schnittpunkt der drei inneren Winkelhalbierenden. Um ihn zu berechnen, lösen wir das Gleichungssystem, das aus zwei Gleichungen besteht.
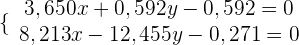
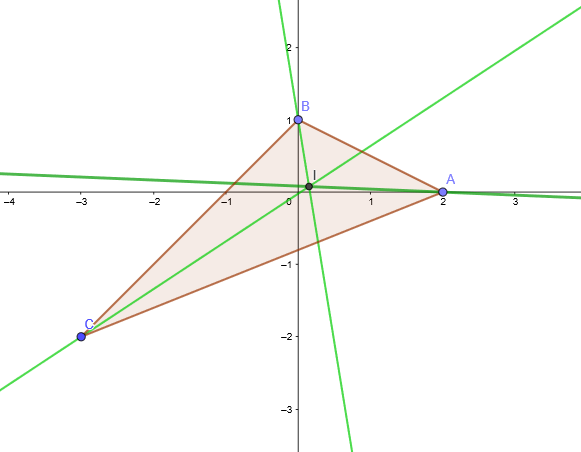
Wir lösen das Gleichungssystem mit 2 Unbekannten und erhalten den Inkreismittelpunkt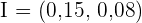
Fläche eines Inkreises
Der Inkreismittelpunkt ist der Mittelpunkt des in das Dreieck eingeschriebenen Kreises, d. h. der Kreis tangiert die drei Seiten des Dreiecks. Der Radius des Kreises ist also der Abstand zwischen dem Inkreismittelpunkt und einer der Seiten.
Um die Fläche des Umkreises zu berechnen, müssen wir zunächst den Radius ermitteln. In diesem Fall berechnen wir den Abstand von  zur Seite
zur Seite 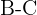 des Dreiecks
des Dreiecks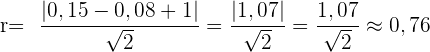
Somit ist die Fläche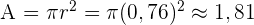
Mit KI zusammenfassen:












