Der Dreisatz gehört zu den nützlichsten Rechenverfahren und den absolut wichtigen Grundlagen der Mathematik. Es handelt sich um eine einfache Methode, um proportionale Zusammenhänge zu berechnen, das können Preis, Dauer oder Gewicht sein.
Ob beim Einkaufen, in der Schule oder im Alltag – überall begegnen dir Verhältnisse, die sich mit dem Dreisatz leicht lösen lassen. In diesem Artikel zeigen wir dir Schritt für Schritt, wie der Dreisatz funktioniert, und geben dir einfache Beispiele zum Mitrechnen.
Wie geht Dreisatz?
Beim Dreisatz geht man in drei Schritten vor, um aus zwei bekannten Werten den dritten zu berechnen. Es geht also darum, eine fehlende Größe zu bestimmen, das ist die Dreisatz Erklärung.
Die Lösung erfolgt in drei Schritten - daher auch der Name.
Die zwei bekannten Größen können proportional oder antiproportional zueinander stehen. Was das genau bedeutet, klären wir jetzt.
Die proportionale Zuordnung
Bei der proportionalen Zuordnung im Dreisatz gilt:
Je mehr von einer Größe, desto mehr (oder weniger im gleichen Verhältnis) von der anderen. Das Verhältnis zwischen beiden Größen bleibt dabei gleich.
Das gehört auf jeden Fall zu den mathematischen Grundrechenarten.
Schauen wir uns dazu einfach ein alltägliches Beispiel an: Du steht im Supermarkt an der Käsetheke und möchtest einen sechs Monate lang gereiften Gouda kaufen. 200g kosten 3,50€. Du möchtest aber 500g kaufen. Wie viel kostet diese Menge?
Hier handelt es sich um eine proportionale Zuordnung: Je mehr Käse Du kaufst, desto mehr musst Du also bezahlen. Um den Preis auszurechnen, wenden wir den Dreisatz an (das Symbol ≙ bedeutet „entspricht“):
- 200g ≙ 3,50€ (hier teilen wir durch 2, um den Preis für 100g auszurechnen)
- 100g ≙ 1,75€ (nun multiplizieren wir mit 5)
- 500g ≙ 8,75€
- Der Preis für 500g Gouda beträgt also 8,75 Euro.
Eine einfache Dreisatz Formel bei proportionaler Zuordnung ist also:
Wenn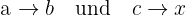 
Dann gilt: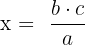 
Wenn beide Größen gleichmäßig steigen oder fallen, liegt eine proportionale Zuordnung vor. Dies kommt oft vor bei:
Menge und Preis
Rezept und Zutaten
Mit Nachhilfe Mathe Berlin kannst Du das üben.
Das Verhältnis ist konstant und lässt sich mit dem Dreisatz einfach berechnen.
Die antiproportionale Zuordnung
Bei der antiproportionalen Zuordnung (auch umgekehrt proportional oder umgekehrte Dreisatz genannt) im Dreisatz verhalten sich zwei Größen gegenteilig:
Wenn eine Größe größer wird, wird die andere kleiner – und umgekehrt. Das Produkt beider Größen bleibt dabei konstant.
Schauen wir uns auch hier ein Beispiel an: Zwei Helfer benötigen für eine Gartenarbeit 6 Stunden. Wie viel Zeit benötigen dann fünf Arbeiter?
Hier handelt es sich um eine antiproportionale Zuordnung, denn je mehr Arbeiter helfen, desto weniger Zeit wird in Anspruch genommen. Schauen wir uns die Rechnung dazu an:
- 2 Personen ≙ 5 Std.
- Um auf 5 Personen zu kommen, muss die 2 mit 2,5 multipliziert werden.
- Um auf die Dauer bei 5 Personen zu kommen, müssen die 5 Std. jedoch nicht mit 2,5 multipliziert sondern durch 2,5 geteilt werden.
- 5 Personen ≙ 2 Std.
Dazu musst Du auch wissen, wie man mit Brüchen rechnen kann.
Eine einfache Dreisatz Formel bei antiproportionaler Zuordnung ist also:
Wenn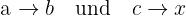 
Dann gilt: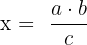 
Wenn eine Größe wächst und die andere im gleichen Maß schrumpft, liegt antiproportionale Zuordnung vor. Dies kommt oft vor bei:
Menge und Preis
Rezept und Zutaten
Auf der rechten Seite musst Du also immer mit dem Gegenteil rechnen, wenn eine antiproportionale Zuordnung vorliegt.
Proportionale Zuordnung - Beispiel
Jetzt, da wir die Dreisatz Erklärung verstanden haben, schauen wir uns einige Beispiele zur proportionalen Zuordnung an.
Beispiel 1
15 Meter Stoff kosten 71,25 Euro. Du möchtest aber nur 9 Meter kaufen. Hier eignet sich die 3 als Zwischenwert (Du teilst also erst durch 5), den Du im dritten Schritt dann mit 3 multiplizierst.
Wir notieren:
- 15m ≙ 71,25€ (wir teilen durch 5)
- 3m ≙ 14,25€ (nun multiplizieren wir mit 3)
- 9m ≙ 42,75€
- 9 Meter Stoff kosten also 42,75 Euro.
Solche eine Aufgabe kannst Du auch mittels einer Bruchgleichung lösen, indem Du nach x auflöst:
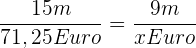Damit x alleine steht und wir nicht viel herumrechnen müssen, nehmen wir von beiden Brüchen den Kehrwert und multiplizieren beide Seiten mit 9:
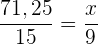und dann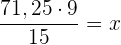 
Das rechnen wir nun aus und erhalten so den Wert von x = 42,75. Es kommt also dasselbe heraus wie mit dem Dreisatz.
Weißt Du, wie man mit Funktionen rechnet?
Beispiel 2
Ein Mann braucht mit dem Auto für eine 60 km lange Strecke 25 Minuten. Eines Tages bleibt sein Auto nach 15 Minuten stehen. Wie viel Kilometer hat er bislang zurückgelegt?
Wir notieren:
- 60 km ≙ 25 Minuten
- Wir teilen beide Seiten durch 5, das ergibt dann: 12 km ≙ 5 Minuten
- Um auf 15 Minuten zu kommen, multiplizieren wir beide Seiten mit 3: 36 km ≙ 15 Minuten
- Der Mann hatte also bereits 36 km zurückgelegt.
Auch bei einer Taxifahrt handelt es sich um einen proportionalen Zusammenhang: Je länger die Strecke, desto höher der Fahrpreis.
Beispiel 3
Du feierst Geburtstag brauchst 18 Euro, um für drei Gäste Snacks und Getränke zu kaufen. Dann entscheidest Du Dich jedoch um und möchtest mit Freunden und Familie zusammen feiern. So kommen noch sechs Leute hinzu. Wie viel Geld benötigst Du, um für alle einzukaufen?
Wir notieren:
- 3 Gäste ≙ 18€
- Da 9 ein Vielfaches der 3 ist, reicht es, die erste Reihe mit der 3 zu multiplizieren, um auf 9 zu kommen
- 9 Gäste ≙ 54€
Mithilfe des Quotienten 
lässt sich die Richtigkeit der Lösung überprüfen.
Mit praktischen Aufgaben kann Nachhilfe Mathe München richtig Spaß machen.
Beispiel 4
Aus dem Wasserhahn laufen in 2 Stunden 200 Liter Wasser. Wie viel Liter laufen in 15 Stunden aus dem Hahn?
Wir notieren:
- 2 Std. ≙ 200 l
- Wir rechnen auf 1 herunter und teilen beide Seiten durch 2
- 1 Std. ≙ 100 l (nun multiplizieren wir mit 15, um auf 15 Std. zu kommen)
- 15 Std. ≙ 1500 l
Mit der Quotientenprobe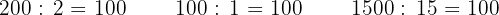 
können wir das Ergebnis überprüfen.
Antiproportionale Zuordnung - Beispiel
Schauen wir uns nun auch zur antiproportionalen Zuordnung einige Beispiele an.
Beispiel 1
Zwei Wasserschläuche brauchen drei Tage, um die Becken des Freibads zu füllen. Wie viele Schläuche werden benötigt, um die Becken in 12 Stunden zu füllen?
Wir notieren:
- 2 Schläuche ≙ 3 Tage
- Wir teilen rechts durch 3 und multiplizieren links mal 3
- 6 Schläuche ≙ 1 Tag
- 12 Stunden sind ein halber Tag, also teilen wir rechts durch 2 und multiplizieren links mal 2
- 12 Schläuche ≙ 0,5 Tage
Um hier das Ergebnis zu überprüfen, musst nicht den Quotienten sondern das Produkt bilden: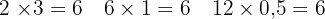 
.
Beispiel 2
Du möchtest Deine Wohnung renovieren lassen und die Malerfirma kann Dir 4 Arbeiter zur Verfügung stellen, die dann 9 Tage fürs Renovieren bräuchten. Du möchtest aber, dass Deine Wohnung schon nach 6 Tagen fertig wird. Wie viel Arbeiter musst Du engagieren?
Wir notieren:
- 4 Arbeiter ≙ 9 Tage
- Wie viel benötigt ein Arbeiter fürs Renovieren: geteilt durch 4 auf der linken Seite und mal 4 auf der rechten Seite
- 1 Arbeiter ≙ 36 Tage (um auf 6 Tage zu kommen, dividieren wir rechts durch 6 und multiplizieren wir links mal 6)
- 6 Arbeiter ≙ 6 Tage
Bilden wir in jeder Reihe das Produkt zur Überprüfung: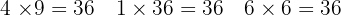 
.
In der Mathe Nachhilfe Leipzig kannst Du diese Beispiele noch einmal üben.
Beispiel 3
Du möchtest Deinen Kleiderschrank sortieren und teilst Deine Kleidung in 7 Stapel à 10 Kleidungsstücke auf. In Deinem Kleiderschrank sind jedoch nur 5 Fächer. Wie viel Kleidungsstücke muss ein Stapel haben, um die Kleidung in 5 Fächern aufzuteilen?
Wir notieren:
- 7 Stapel ≙ 10 Kleidungsstücke
- Wir rechnen auf 35 Stapel hoch, um später auf 5 herunterrechnen zu können. Dazu multiplizieren wir links mit 5 und dividieren rechts durch 5)
- 35 Stapel ≙ 2 Kleidungsstücke (um nun auf 5 Stapel zu kommen, dividieren wir links durch 7 und multiplizieren rechts mit 7)
- 5 Stapel ≙ 14 Kleidungsstücke
Multiplizieren wir die Zahlen zur Probe: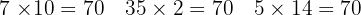 
.
Um den Dreisatz zu beherrschen, solltest Du diese proportionalen und anti-proportionalen Zuordnungen oft üben.
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
