Probleme zu Exponentialfunktionen
Exponentialfunktionen sind Funktionen, bei denen die unabhängige Variable z. B. im Exponenten zu finden ist:
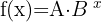
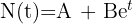
Es gibt mehrere mathematische Modelle, die es uns ermöglichen, bestimmte Phänomene mit einer Exponentialfunktion zu beschreiben.
Radioaktiver Zerfall
In einer Probe eines Fossils wurde festgestellt, dass 0,003 % des enthaltenen Kohlenstoffs Kohlenstoff 14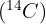 
ist. Wenn bekannt ist, dass 
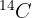1 % des in einem Lebewesen vorhandenen Kohlenstoffs ausmacht und dass die Halbwertszeit von 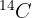5730 Jahre beträgt, wie alt ist dann das Fossil?
1 Für den radioaktiven Zerfall gilt die folgende Exponentialfunktion
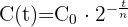
Wobei:
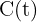ist die Menge des radioaktiven Isotops zum Zeitpunkt 't'
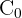ist die ursprüngliche Menge an 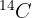in der Probe
ist die Halbwertszeit des radioaktiven Isotops in Jahren
ist die verstrichene Zeit in Jahren
2 Wir ermitteln die Variable der Exponentialfunktion
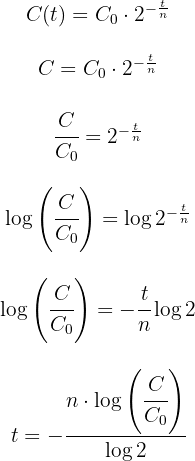
3 Wir setzen die Werte ein und führen die Berechnungen durch, um den Wert von zu erhalten
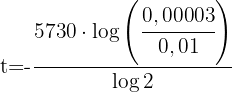
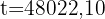
4 Das Fossil ist 48022 Jahre alt
Wachstum einer Population
Wir wissen, dass die Anzahl 'N' der Insekten in 't' Jahren durch eine Exponentialfunktion des Typs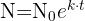 
gegeben ist. Eine Gruppe von Biologen schätzt, dass die Population in den letzten drei Jahren um 20 % zugenommen hat, und sie wissen, dass sie zu einer Plage wird, wenn die Population um 70 % gegenüber der ursprünglichen Population ansteigt. In wie vielen Jahren wird die Insektenpopulation schätzungsweise zu einer Plage?
1 Da wir den Wert der Konstante 'k' nicht kennen, müssen wir die uns gegebenen Werte verwenden, um ihn zu erhalten. Also ermitteln wir zunächst 'k'
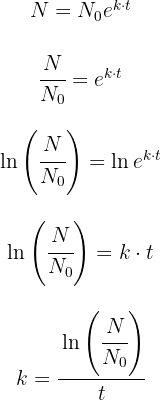
2 Wir setzen die erhaltenen Werte ein und berechnen den Wert von 'k'
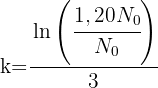
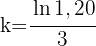
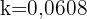
3 Die Exponentialfunktion lautet
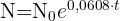
4 Wir ermitteln die Variable 't'
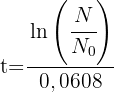
5 Wir setzen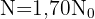 
ein und lösen
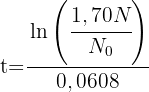
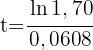
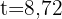
6 Die Population wächst um 70 % in 8,72 Jahren
Das Bevölkerungswachstum kann durch eine logistische Wachstumsfunktion beschrieben werden. Für die Bevölkerung einer Karibikinsel lässt sich bekanntlich die Funktion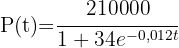 
festlegen und 
entspricht der Bevölkerung der Insel im Jahr 2000.
AWie viele Einwohner wird es im Jahr 2025 geben?
B In wie vielen Jahren wird sich die Bevölkerung gegenüber dem Jahr 2020 verdoppeln?
A Wie viele Einwohner wird es im Jahr 2025 geben?
1 Wir setzen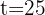 
in die Funktion ein und lösen
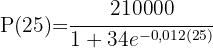
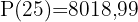
BIn wie vielen Jahren wird sich die Bevölkerung gegenüber dem Jahr 2020 verdoppeln?
1 Wir berechnen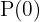 
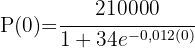
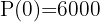
2 Wir ermitteln die Variable 't'
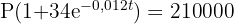
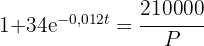
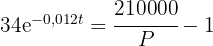
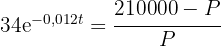
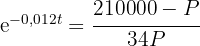
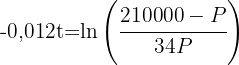
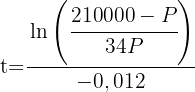
3 Wir setze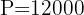n 
ein
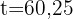
4 Die Bevölkerung wird sich bis etwa 2060 verdoppeln.
Newtonsches Abkühlungsgesetz
Die Körpertemperatur eines Menschen beträgt 37°C. Es ist bekannt, dass es beim Tod eines Menschen durchschnittlich 20 Stunden dauert, bis seine Körpertemperatur 27°C erreicht, wenn die Umgebungstemperatur bei 25°C bleibt. Wenn der menschliche Körper dem Newtonschen Abkühlungsgesetz folgt, gilt:
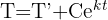
T ist die Temperatur zum Zeitpunkt 't' und T' die Umgebungstemperatur.
Ein Gerichtsmediziner stellt fest, dass die Temperatur einer verstorbenen Person 29°C beträgt und die Umgebungstemperatur seit dem Tod bei 25°C geblieben ist. Wenn es auf der Uhr des Arztes 19:00 Uhr ist, was ist dann der geschätzte Todeszeitpunkt?
1 Mit den in der Aufgabenstellung angegebenen Werten können wir den Wert der Konstanten 'C' und 'k' berechnen. Zunächst werten wir die Funktion für aus
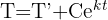
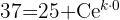
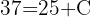
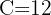
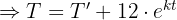
2 Wir ermitteln die Konstante 'k' und setzen die Werte ein, wenn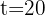 
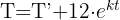
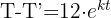
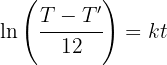
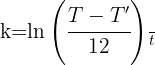
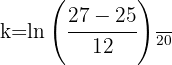
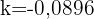
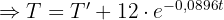
4 Aus der resultierenden Funktion erhalten wir 't' und setzen die Werte ein, wenn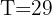 
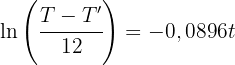
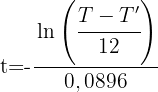
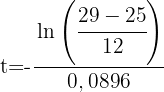
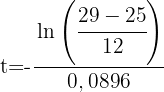
Es sind etwa 12,26 Stunden vergangen
5 Die Person starb kurz vor 7:00 Uhr morgens.
Zinseszins
Eine Person legt ein Kapital von 3200 Euro bei einer Bank an, die einen jährlichen Zinssatz von 7,5 % bietet.
A Wie hoch wird das Kapital in 3 Jahren sein?
B In wie vielen Jahren beträgt das Kapital 5000 Euro?
AWie hoch wird das Kapital in 3 Jahren sein?
1 Die Formel für die Berechnung der Zinseszinsen lautet
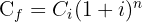
2 Wir setzen die Werte ein, um das Endkapital zu berechnen
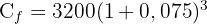
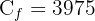
3 In drei Jahren beträgt das Kapital 3975 Euro
B In wie vielen Jahren beträgt das Kapital 5000 Euro?
1 Wir ermitteln die Variable 'n' der Funktion
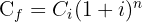
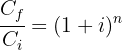
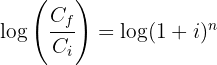
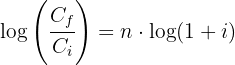
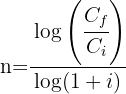
2 Wir setzen die Werte ein, um den Wert von 'n' zu ermitteln
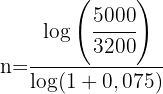
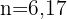
3 Es dauert noch 6 Jahre, bis das Kapital 5000 Euro beträgt
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
