Definition von Asymptoten
Die Asymptoten sind Geraden, denen sich die Funktion auf unbestimmte Zeit nähert.
Es gibt drei Arten von Asymptoten:
1 Waagerechte
2 Senkrechte
3 Schräge
Waagrechte Asymptoten
Wenn eine der beiden folgenden Bedingungen erfüllt ist
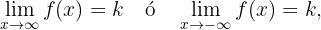
dann ist die Gerade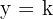 
eine horizontale Asymptote für den Graphen von 
Beispiel: Berechne die waagrechten Asymptoten der Funktion 
Berechne den Grenzwert, wenn 
gegen 
tendiert, indem Du jeden Term des Zählers und Nenners durch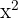 
dividierst
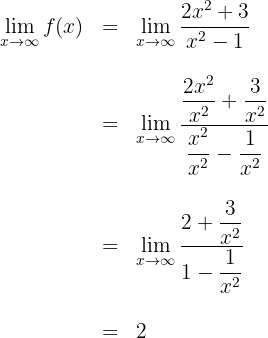
Die Funktion hat also eine waagrechte Asymptote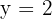 
Senkrechte Asymptoten
Wenn eine der beiden folgenden Bedingungen erfüllt ist
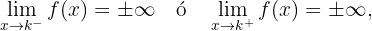
dann ist die Gerade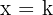 
eine senkrechte Asymptote für den Graphen von
Beachte, dass 
die Punkte sind, die nicht zum Bereich der Funktion gehören (bei rationalen Funktionen)
Beispiel: Berechne die vertikalen Asymptoten der Funktion
Der Bereich der Funktion ist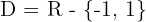 
Berechne die seitlichen Grenzen, wenn gegen 
tendiert
Die Funktion hat also eine senkrechte Asymptote 
Berechne die seitlichen Grenzen, wenn tiende a 
tendiert
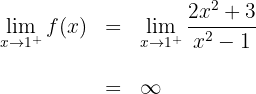
Die Funktion hat also eine weitere senkrechte Asymptote 
Dies geht aus dem Graphen der Funktion hervor
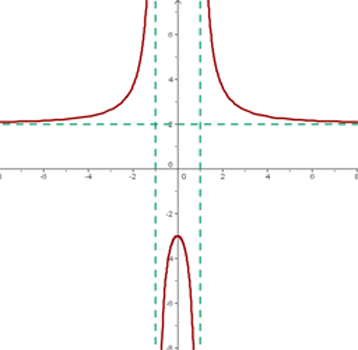
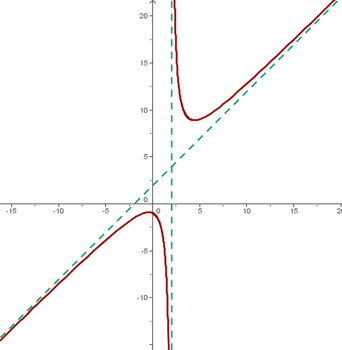
Schräge Asymptoten
Schräge Asymptoten werden nur gefunden, wenn es keine waagrechten Asymptoten gibt.
Damit es eine schräge Asymptote gibt, muss der Grad des Zählers genau einen Grad größer sein als der des Nenners, so dass die Asymptote gegeben ist durch
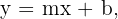
wobei
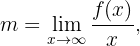
Beispiel: Berechne die vertikalen Asymptoten der Funktion 
Wenn sichergestellt ist, dass der Grad des Zählers genau einen Grad größer ist als der des Nenners, bleibt nur noch zu überprüfen, ob es waagrechte Asymptoten gibt.
Berechne den Grenzwert, wenn gegen , tendiert, indem Du jeden Term des Zählers und Nenners durch 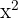teilst
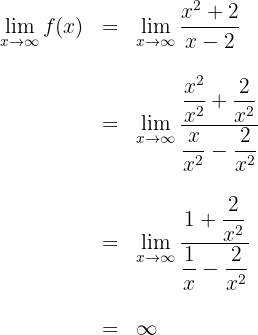
Die Funktion hat also keine waagrechten Asymptoten.
Um zu sehen, ob sie schräge Asymptoten hat, berechnest Du
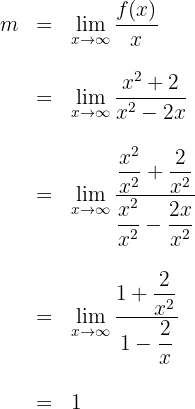
Die schräge Asymptote ist also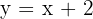 
Du stellst fest, dass der Bereich der Funktion 
und 
eine vertikale Asymptote ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
