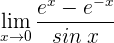
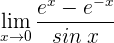
1 Wir haben den unbestimmten Ausdruck 
2 Wir wenden die Regel von de L’Hospital an
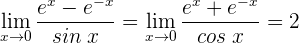
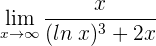
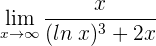
1 Wir haben den unbestimmten Ausdruck 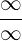
2 Wir wenden die Regel von de L’Hospital an

3 Vergleicht man die Unendlichkeiten für  , so stellt man fest, dass der Zähler eine Unendlichkeit niedrigerer Ordnung ist als der Nenner, so dass der Grenzwert 0 ist.
, so stellt man fest, dass der Zähler eine Unendlichkeit niedrigerer Ordnung ist als der Nenner, so dass der Grenzwert 0 ist.
4 Somit ist das Ergebnis
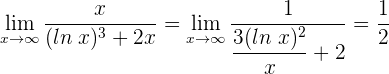
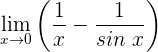
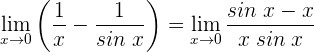
1 Wir haben den unbestimmten Ausdruck 
2 Wir wenden die Regel von de L’Hospital an
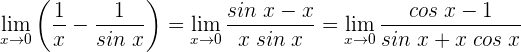
3 Wir erhalten erneut einen unbestimmten Ausdruck 
4 Wir wenden die Regel von de L’Hospital an
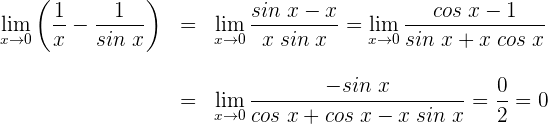
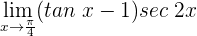
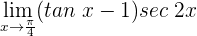
1 Wir setzen ein und erhalten 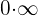 . Wir wenden die trigonometrische Beziehung
. Wir wenden die trigonometrische Beziehung 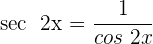 an
an
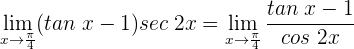
2 Wir haben den unbestimmten Ausdruck 
3 Wir wenden die Regel von de L’Hospital an
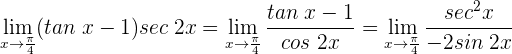
4 Wir wenden die trigonometrische Beziehung 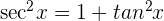 an
an
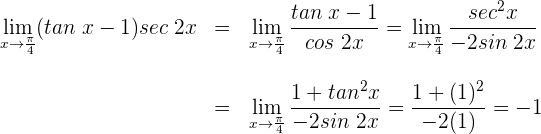
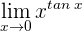
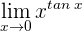
1 Wir setzen ein und erhalten  . Daher wenden wir die Gesetze zum Rechnen mit Logarithmus- und Exponentialfunktionen an, um
. Daher wenden wir die Gesetze zum Rechnen mit Logarithmus- und Exponentialfunktionen an, um 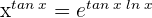 zu erhalten. Der Grenzwert wird also zu
zu erhalten. Der Grenzwert wird also zu
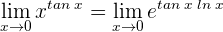
2 Gemäß den Eigenschaften des Grenzwerts für eine stetige Funktion ergibt sich
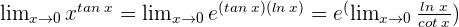
3 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
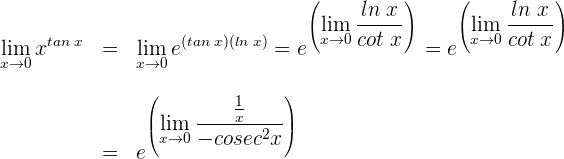
4 Wir wenden die trigonometrische Beziehung 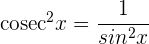 an
an
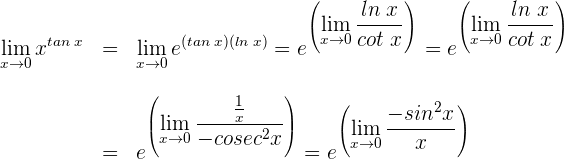
5 Wir haben den unbestimmten Ausdruck 
6 Wir wenden die Regel von de L’Hospital an
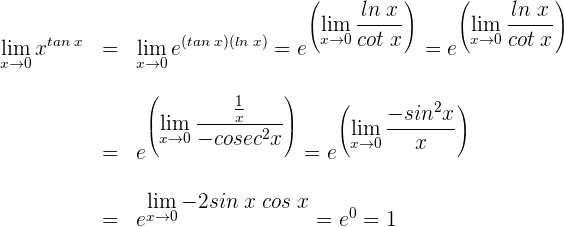
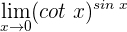
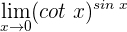
1 Wir setzen ein und erhalten einen unbestimmten Ausdruck. Daher wenden wir die Regeln zum Rechnen mit Logarithmus- und Exponentialfunktionen an, um 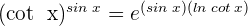 zu erhalten. Der Grenzwert wird also zu
zu erhalten. Der Grenzwert wird also zu
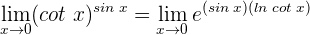
2 Wir wenden die trigonometrische Beziehung 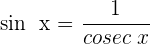 an
an
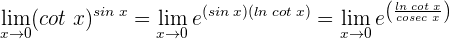
3 Gemäß den Eigenschaften des Grenzwerts für eine stetige Funktion ergibt sich
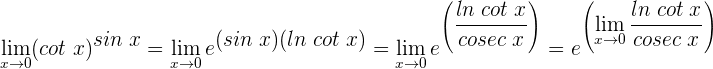
4 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
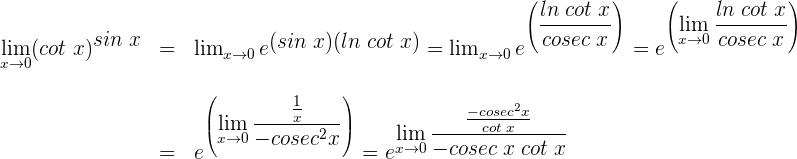
5 Wir vereinfachen und wenden die trigonometrische Beziehung 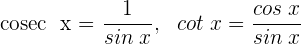 an
an
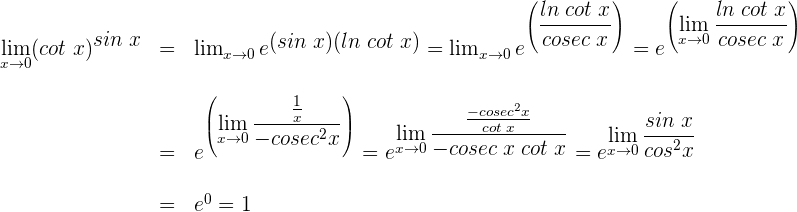


1 Wir setzen ein und erhalten einen unbestimmten Ausdruck. Daher wenden wir die Regeln zum Rechnen mit Logarithmus- und Exponentialfunktionen an, um  zu erhalten
zu erhalten

2 Gemäß den Eigenschaften des Grenzwerts für eine stetige Funktion ergibt sich
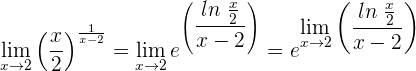
3 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
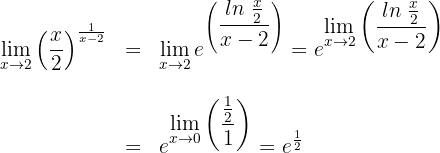
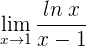
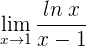
1 Wir setzen ein und erhalten einen unbestimmten Ausdruck 
2 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
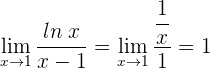
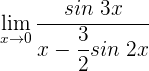
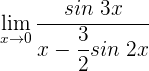
1 Wir setzen ein und erhalten einen unbestimmten Ausdruck 
2 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
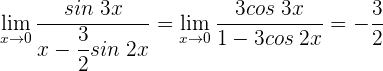
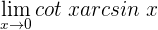
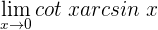
1 Wir wenden die trigonometrischen Beziehungen
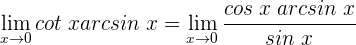 an
an
2 Wir setzen ein und erhalten einen unbestimmten Ausdruck 
3 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
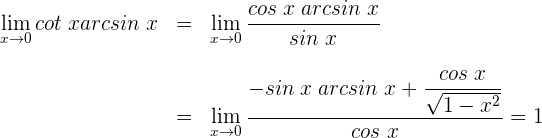
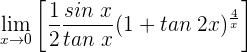
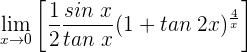
1 Wir wenden die trigonometrischen Beziehungen und die Regeln für den Grenzwert an
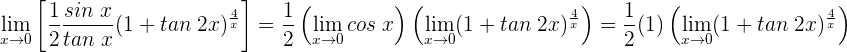
2 Wir setzen ein und erhalten einen unbestimmten Ausdruck. Daher wenden wir die Regeln zum Rechnen mit Logarithmus- und Exponentialfunktionen sowie die Regel von de L'Hospital an
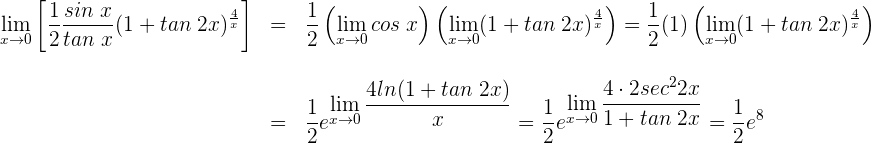
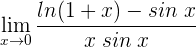
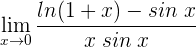
1 Wir setzen ein und erhalten einen unbestimmten Ausdruck 
2 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
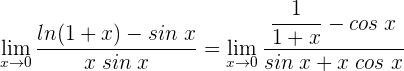
3 Wir erhalten erneut einen unbestimmten Ausdruck und wenden deshalb die Regel von de L'Hospital an.
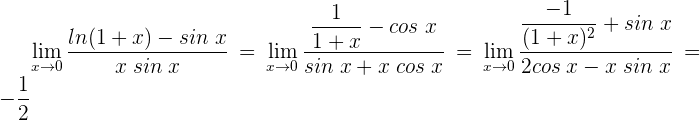
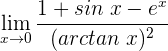
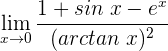
1 Wir setzen ein und erhalten einen unbestimmten Ausdruck 
2 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
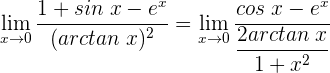
3 Wir erhalten erneut einen unbestimmten Ausdruck und wenden daher die Regel von de L'Hospital an
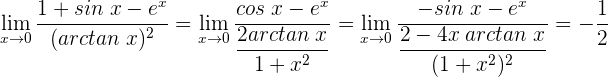

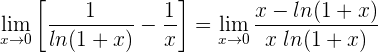
1 Wir setzen ein und erhalten einen unbestimmten Ausdruck 
2 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
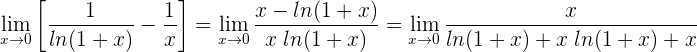
3 Wir erhalten erneut einen unbestimmten Ausdruck und wenden daher die Regel von de L'Hospital an

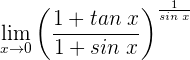
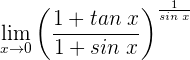
1 Wir setzen ein und erhalten einen unbestimmten Ausdruck. Daher wenden wir die Regeln zum Rechnen mit Logarithmus- und Exponentialfunktionen sowie die Regel von de L'Hospital an
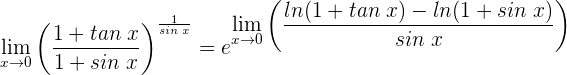
2 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
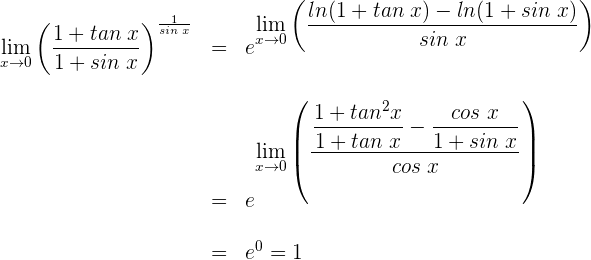
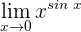
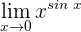
1 Wir setzen ein und erhalten einen unbestimmten Ausdruck. Daher wenden wir die Regeln zum Rechnen mit Logarithmus- und Exponentialfunktionen an
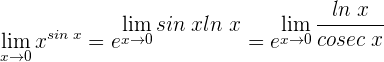
2 Wir wenden die Regel von de L’Hospital an, da wir einen unbestimmten Ausdruck haben
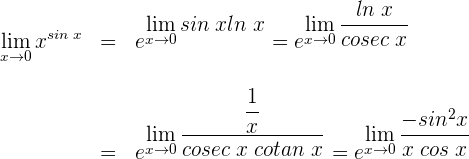
3 Wir erhalten einen unbestimmten Ausdruck und wenden daher erneut die Regel von de L'Hospital an
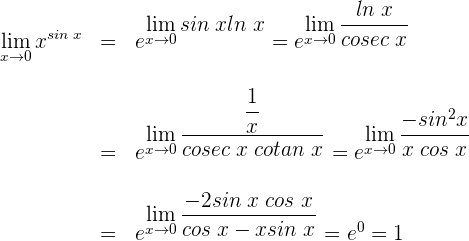
Mit KI zusammenfassen:


