Berechne die relative Lage des Kreises 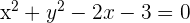 und der Geraden
und der Geraden 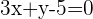 .
.
Berechne die relative Lage des Kreises 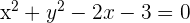 und der Geraden
und der Geraden 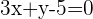 .
.
1 Wir stellen ein Gleichungssystem zwischen der Gleichung des Kreises und der Gleichung der Geraden auf
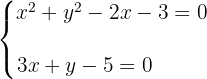
2 Um das Gleichungssystem zu lösen, ist es am einfachsten, die Variable  aus der zweiten Gleichung zu eliminieren und sie in die erste Gleichung einzusetzen
aus der zweiten Gleichung zu eliminieren und sie in die erste Gleichung einzusetzen
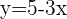 setzen wir in die 1. Gleichung ein:
setzen wir in die 1. Gleichung ein:

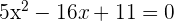

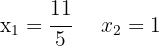
3 Wir setzen die Werte von  in die Gleichung der Geraden ein, um die Koordinaten der Schnittpunkte zu erhalten
in die Gleichung der Geraden ein, um die Koordinaten der Schnittpunkte zu erhalten
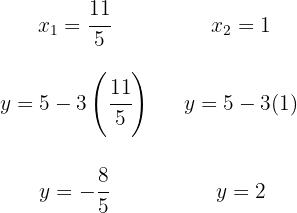
Die Schnittpunkte sind  und
und 
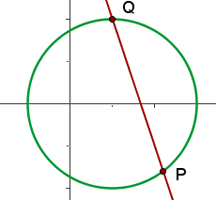
Da es 2 Schnittpunkte gibt, ist die Gerade eine Sekante des Kreises.
2 Untersuche die relative Lage des Kreises 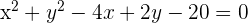 mit den Geraden:
mit den Geraden:
A 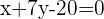
B 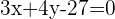
C 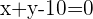
Untersuche die relative Lage des Kreises 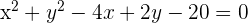 mit den Geraden:
mit den Geraden:
A 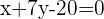
1 Wir stellen ein Gleichungssystem mit dem Kreis und der Geraden auf
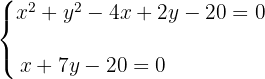
2 Um das System zu lösen, ermitteln wir  aus der Geradengleichung und setzen es in die Kreisgleichung ein
aus der Geradengleichung und setzen es in die Kreisgleichung ein

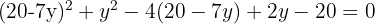
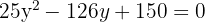
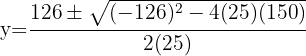

3 Wir setzen die erhaltenen Werte von  in den Ausdruck von
in den Ausdruck von  ein
ein
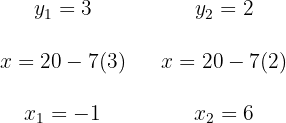
Die Schnittpunkte sind 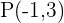 und
und 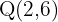
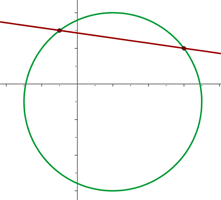
Da es zwei Schnittpunkte gibt, ist die Gerade eine Sekante des Kreises.
B 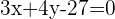
1 Wir stellen ein Gleichungssystem mit dem Kreis und der Geraden auf

2 Um das System zu lösen, bestimmen wir  aus der Geradengleichung und setzen es in die Kreisgleichung ein
aus der Geradengleichung und setzen es in die Kreisgleichung ein
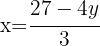

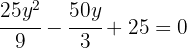
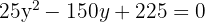
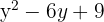


3 Wir setzen den erhaltenen Wert von  ein, um die Koordinaten des Schnittpunkts zu erhalten
ein, um die Koordinaten des Schnittpunkts zu erhalten


Der Schnittpunkt des Kreises mit der Geraden ist 
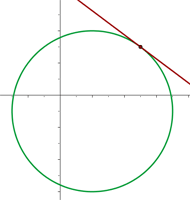
Da es nur einen Schnittpunkt gibt, ist die Gerade eine Tangente an den Kreis
C 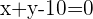
1 Wir stellen ein Gleichungssystem mit dem Kreis und der Geraden auf
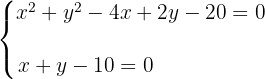
2 Um das System zu lösen, bestimmen wir  aus der Geradengleichung und setzen es in die Kreisgleichung ein
aus der Geradengleichung und setzen es in die Kreisgleichung ein
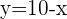
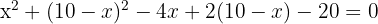


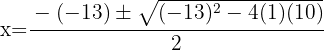
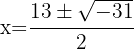
Da die quadratische Gleichung keine Lösung hat, gibt es keinen Schnittpunkt zwischen dem Kreis und der Geraden
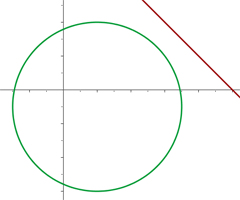
Da es keinen Schnittpunkt gibt, befindet sich die Gerade außerhalb des Kreises.
Bestimme die relative Lage der Geraden 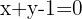 mit der Hyperbel
mit der Hyperbel 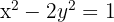
Bestimme die relative Lage der Geraden 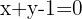 mit der Hyperbel
mit der Hyperbel 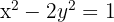
1 Wir stellen ein Gleichungssystem mit der Hyperbel und der Geraden auf

2 Um das System zu lösen, bestimmen wir  aus der Gleichung der Geraden und setzen es in die Gleichung der Hyperbel ein
aus der Gleichung der Geraden und setzen es in die Gleichung der Hyperbel ein
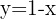
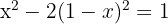

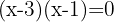

3 Wir setzen den erhaltenen Wert von  ein, um die Koordinaten der Schnittpunkte zu erhalten
ein, um die Koordinaten der Schnittpunkte zu erhalten
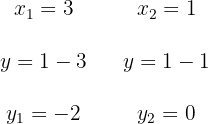
Die Schnittpunkte zwischen der Hyperbel und der Geraden sind 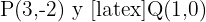
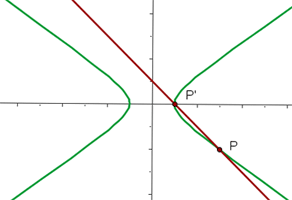
Da es 2 Schnittpunkte gibt, sind die Gerade und die Hyperbel Sekanten.
Berechne die relative Lage der Geraden 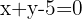 in Bezug auf die Parabel
in Bezug auf die Parabel 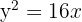
Berechne die relative Lage der Geraden 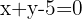 in Bezug auf die Parabel
in Bezug auf die Parabel 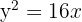
1 Wir stellen ein Gleichungssystem mit der Parabel und der Geraden auf
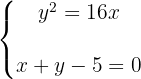
2 Um das System zu lösen, bestimmen wir  aus der Gleichung der Geraden und setzen es in die Gleichung der Parabel ein
aus der Gleichung der Geraden und setzen es in die Gleichung der Parabel ein
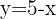
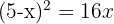



3 Wir setzen den erhaltenen Wert von  ein, um die Koordinaten der Schnittpunkte zu erhalten
ein, um die Koordinaten der Schnittpunkte zu erhalten
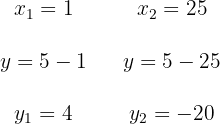
Die Schnittpunkte sind 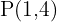 und
und 
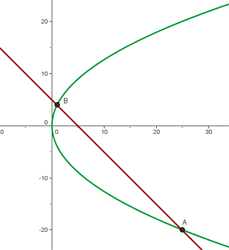
Da es zwei Schnittpunkte gibt, sind die Gerade und die Parabel Sekanten
Mit KI zusammenfassen:


