Bestimme die Punkte der Stetigkeit der Funktion 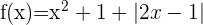
Bestimme die Punkte der Stetigkeit der Funktion 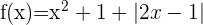
1 Wir wandeln die Funktion in eine abschnittsweise definierte Funktion um
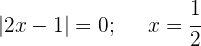
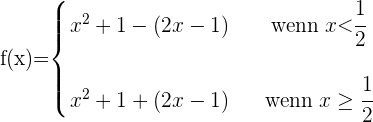
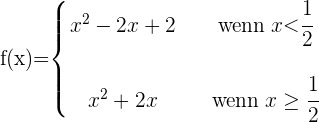
2 Wir untersuchen die Stetigkeit bei 
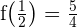
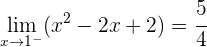

Die Funktion ist stetig im gesamten Bereich  .
.
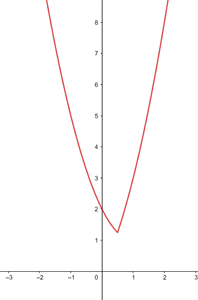
Gegeben ist die Funktion
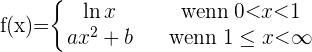
Wenn 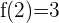 , bestimme die Werte von
, bestimme die Werte von  und
und  , sodass
, sodass  stetig ist.
stetig ist.
Gegeben ist folgende Funktion
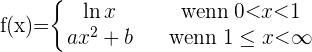
Wenn 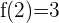 , bestimme die Werte von
, bestimme die Werte von  und
und  , sodass
, sodass  stetig ist.
stetig ist.
1 Zweifel an der Stetigkeit gibt es nur bei  .
.


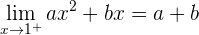
2 Damit die Funktion stetig ist, muss Folgendes erfüllt sein:

3 Auf der anderen Seite haben wir:
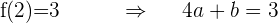
4 Wir lösen das Gleichungssystem und erhalten:

Gegeben ist die Funktion:
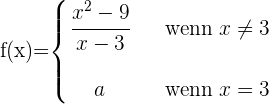
Bestimme den Wert von a, sodass die Funktion für  stetig ist.
stetig ist.
Gegeben ist die Funktion:
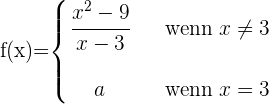
Bestimme den Wert von a, sodass die Funktion für  stetig ist.
stetig ist.
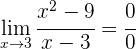
1 Wir lösen den unbestimmten Ausdruck, indem wie den Zähler in Faktoren zerlegen und den Bruch vereinfachen
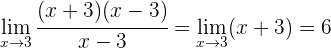
2 Um bei  stetig zu sein, muss der Grenzwert, wenn
stetig zu sein, muss der Grenzwert, wenn  gegen
gegen  läuft, gleich der Abbildung von
läuft, gleich der Abbildung von  sein.
sein.
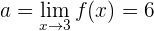
Gegeben ist die Funktion:
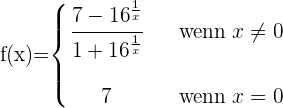
Ermittle die Punkte der Stetigkeit
Gegeben ist die Funktion:
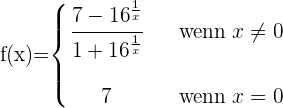
Ermittle die Punkte der Stetigkeit
1 Die Exponentialfunktion ist für gesamt 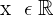 positiv, weshalb der Nenner der Funktion nicht null werden kann.
positiv, weshalb der Nenner der Funktion nicht null werden kann.
Einen Zweifel an der Stetigkeit gibt es nur bei  .
.


2 Wir lösen den unbestimmten Ausdruck, indem wir durch 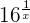 dividieren
dividieren
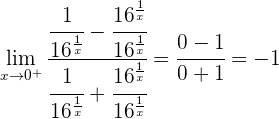
3 Die seitlichen Grenzwerte fallen nicht zusammen, sodass bei  keine Stetigkeit vorliegt.
keine Stetigkeit vorliegt.
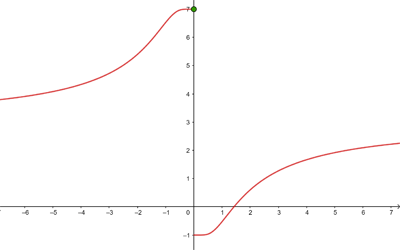
Die Funktion ist stetig im Bereich  .
.
Gegeben ist die Funktion
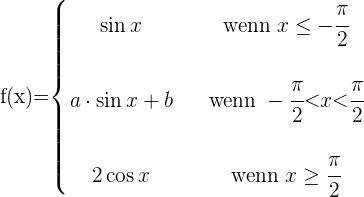
Bestimme  und
und  so, dass die Funktion
so, dass die Funktion  für alle Werte von
für alle Werte von  stetig ist.
stetig ist.
Gegeben ist die Funktion
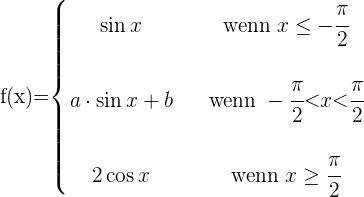
Bestimme  und
und  so, dass die Funktion
so, dass die Funktion  für alle Werte von
für alle Werte von  stetig ist.
stetig ist.
1 Die Abbildung von 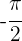 ist gleich dem Grenzwert auf der linken Seite
ist gleich dem Grenzwert auf der linken Seite

2 Die Abbildung von 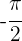 ist gleich dem Grenzwert auf der rechten Seite
ist gleich dem Grenzwert auf der rechten Seite
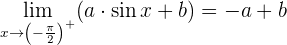
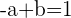
3 Die Abbildung von  ist gleich dem Grenzwert auf der linken Seite
ist gleich dem Grenzwert auf der linken Seite
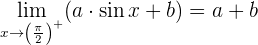
4 Die Abbildung von  ist gleich dem Grenzwert auf der rechten Seite
ist gleich dem Grenzwert auf der rechten Seite


5 Wir lösen das Gleichungssystem nach  und
und  auf
auf
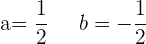
Gegeben ist die Funktion:
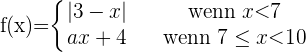
Bestimme den Wert von  , sodass
, sodass  stetig ist.
stetig ist.
Gegeben ist die Funktion:
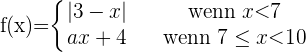
Bestimme den Wert von  , sodass
, sodass  stetig ist.
stetig ist.
1 Bei dieser abschnittsweise definierten Funktion sind die beiden Teilfunktionen in ihren Definitionsbereichen stetig. Wir untersuchen das Verhalten der Funktion am Punkt der Vereinigung.
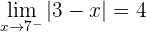
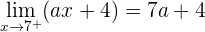

Berechne den Wert von  , sodass die folgende Funktion stetig ist.
, sodass die folgende Funktion stetig ist.
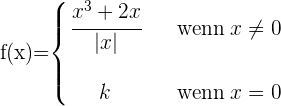
Berechne den Wert von  , sodass die folgende Funktion stetig ist.
, sodass die folgende Funktion stetig ist.
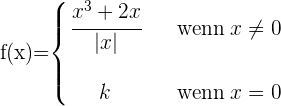
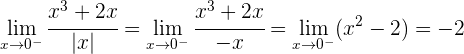
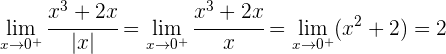
Es existiert also kein Grenzwert bei 
Es ist nicht möglich, dass  bei
bei  stetig ist, egal welchen Wert man
stetig ist, egal welchen Wert man  zuweist.
zuweist.
Gegeben ist die Funktion:
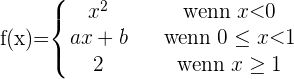
Bestimme  und
und  , sodass die Funktion stetig ist.
, sodass die Funktion stetig ist.
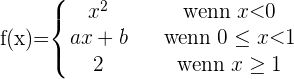
Bestimme  und
und  , sodass die Funktion stetig ist.
, sodass die Funktion stetig ist.
1 Wir untersuchen die Stetigkeit bei 
 -
-
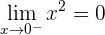
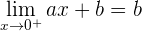

2 Wir untersuchen die Stetigkeit bei 



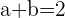

Berechne die Werte von  und
und  , sodass die folgende Funktion stetig ist.
, sodass die folgende Funktion stetig ist.
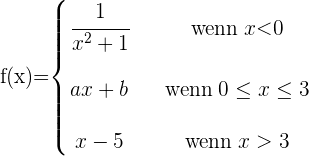
Berechne die Werte von  und
und  , sodass die folgende Funktion stetig ist.
, sodass die folgende Funktion stetig ist.
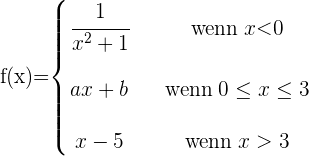
Wir untersuchen die Stetigkeit bei 

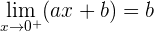
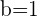
Wir untersuchen die Stetigkeit bei 
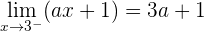
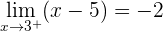

Mit KI zusammenfassen:


