Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:

Die Definitionsmenge der Funktion ist  .
.
Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
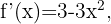

Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte

Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist

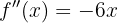 konkav auf
konkav auf  und konvex auf
und konvex auf 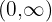 ist.
ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:
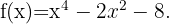
Die Definitionsmenge der Funktion ist  . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
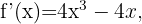
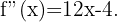
Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
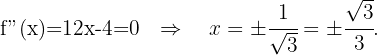
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
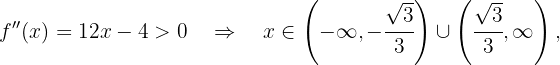
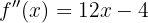 konvex auf
konvex auf 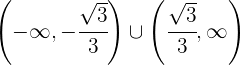 und konkav auf
und konkav auf 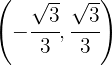 ist.
ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:
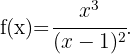
Die Definitionsmenge der Funktion ist 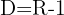 . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
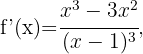
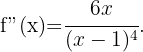
Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
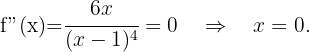
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist

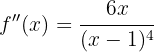 konvex auf
konvex auf  und konkav auf
und konkav auf 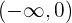 ist.
ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:

Die Definitionsmenge der Funktion ist 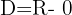 . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung

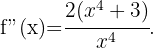
Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
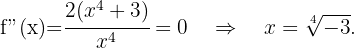
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
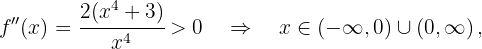
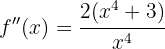 konvex auf
konvex auf 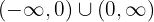 ist und keine Intervalle hat, auf denen sie konkav ist.
ist und keine Intervalle hat, auf denen sie konkav ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:
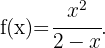
Die Definitionsmenge der Funktion ist 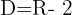 . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung


Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
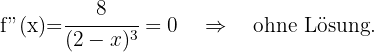
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist

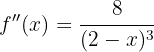 konvex auf
konvex auf 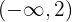 und konkav auf
und konkav auf 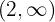 ist.
ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:
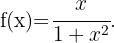
Die Definitionsmenge der Funktion ist  . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
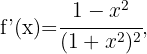

Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
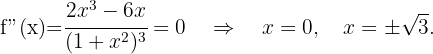
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
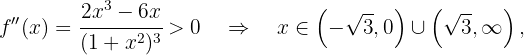
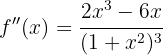 konvex auf
konvex auf  und konkav auf
und konkav auf 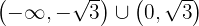 ist.
ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:
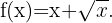
Die Definitionsmenge der Funktion ist 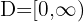 . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
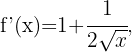
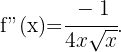
Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
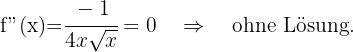
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
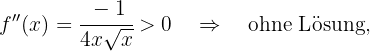
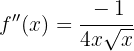 keine Intervalle hat, auf denen sie konvex ist. Sie ist konkav auf
keine Intervalle hat, auf denen sie konvex ist. Sie ist konkav auf 
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:

Die Definitionsmenge der Funktion ist  . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
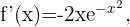

Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
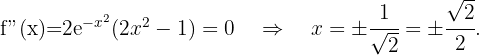
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
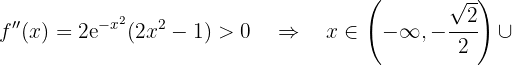
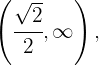
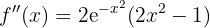 konvex auf
konvex auf 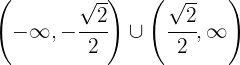 und konkav auf
und konkav auf 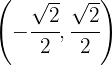 ist.
ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:

Die Definitionsmenge der Funktion ist 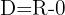 . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
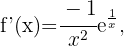
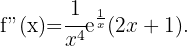
Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
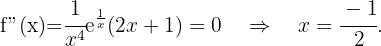
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
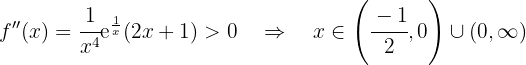
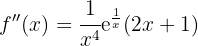 konvex auf
konvex auf 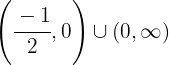 und konkav auf
und konkav auf  ist
ist
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:
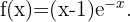
Die Definitionsmenge der Funktion ist 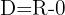 . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
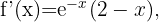
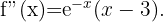
Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
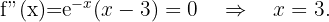
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
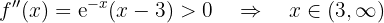
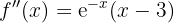 konvex auf
konvex auf 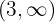 und konkav auf
und konkav auf 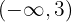 ist.
ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:
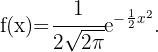
Die Definitionsmenge der Funktion ist  . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
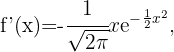
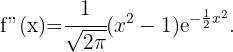
Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
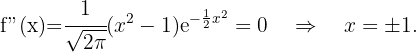
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
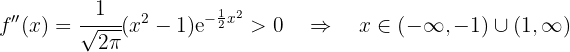
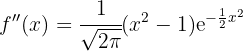 konvex auf
konvex auf  und konkav auf
und konkav auf 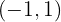 ist.
ist.
Ermittle die Intervalle, auf denen die folgende Funktion konkav oder konvex ist:

Die Definitionsmenge der Funktion ist 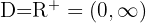 . Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
. Wir wenden nun das Konkavitäts-Konvexitäts-Kriterium der 2. Ableitung an, das besagt, dass die Funktion auf den Intervallen konvex ist, auf denen die 2. Ableitung positiv ist, und auf den Intervallen, auf denen die 2. Ableitung negativ ist, konkav ist.
Wir berechnen zunächst die 2. Ableitung
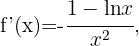
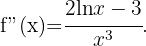
Danach ermitteln wir die Punkte, an denen die 2. Ableitung 0 wird.
Wir erhalten die Wendepunkte
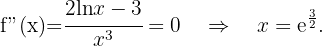
Zum Schluss analysieren wir, auf welchen Intervallen die 2. Ableitung positiv oder negativ ist
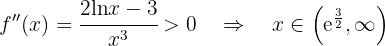
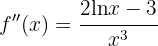 konvex auf
konvex auf 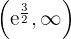 und konkav auf
und konkav auf 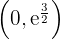 ist.
ist.
Mit KI zusammenfassen:


