Willkommen auf unserer Seite, die den Übungen zu Maxima und Minima gewidmet ist! In diesem Bereich werden wir das spannende Gebiet der mathematischen Optimierung erkunden und dir das Wissen und die Strategien vermitteln, die du brauchst, um Probleme zu lösen, bei denen es darum geht, die Maximal- und Minimalwerte von Funktionen zu ermitteln.
Probleme mit Maxima und Minima treten in einer Vielzahl von Bereichen auf, z. B. in der Physik, den Wirtschaftswissenschaften, dem Ingenieurwesen und vielen anderen. Bei diesen Aufgaben geht es darum, die kritischen Punkte einer Funktion zu finden, bei denen die Steigung gleich Null ist, und zu bestimmen, ob diese Punkte lokalen Maxima oder Minima entsprechen.
Hier lernst du, die wichtigsten Eigenschaften einer Funktion zu identifizieren, die es dir ermöglichen, ihre Maxima und Minima zu bestimmen. Dazu werden wir dir eine Vielzahl von Aufgaben zur Verfügung stellen, die wir mit Hilfe der zweiten Ableitung lösen werden.
Unser Ziel ist es, dich dabei zu unterstützen, deine Fähigkeiten zu stärken, optimale Lösungen zu finden, dein analytisches Denken zu verbessern und dein Selbstbewusstsein in der Mathematik zu fördern. Viel Spaß beim Lernen mit den verschiedenen Übungen und den klaren und detaillierten Erklärungen, die wir für dich erstellt haben. Werde Profi in der Berechnung von Maxima und Minima von Funktionen!
Nutze die zweite Ableitung, um die lokalen Maxima und Minima der folgenden Funktionen zu berechnen:
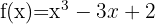
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion:
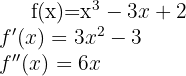
Wir bestimmen nun die kritischen Punkte 
durch die Lösung (oder Lösungen) der Gleichung 
, also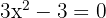 
. Die Lösungen dieser Gleichung sind 
.
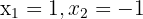Schließlich werten wir 
an den kritischen Punkten aus und ermitteln, ob 
oder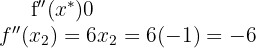 
ein lokales Minimum bei 
und ein lokales Maximum bei 
hat. Die entsprechenden Werte der Funktion sind:
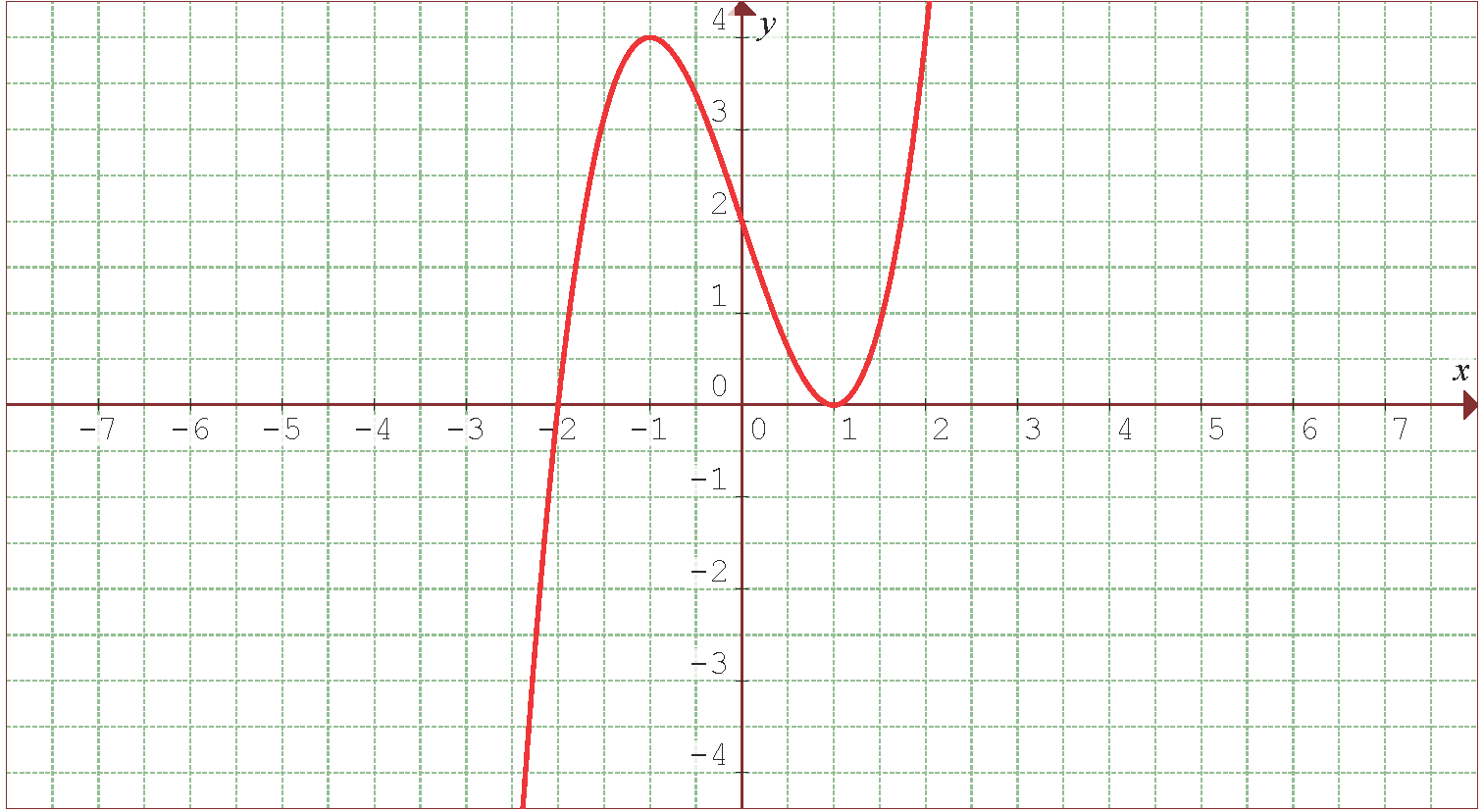
Folgende Abbildung zeigt den Graphen der Funktion 
.
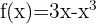
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion:
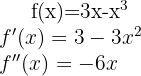
Wir bestimmen nun die kritischen Punkte durch die Lösung (oder Lösungen) der Gleichung , also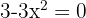 
. Die Lösungen dieser Gleichung lauten 
.
Schließlich werten wir an den kritischen Punkten aus und ermitteln, ob oder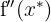 
Die 2. Ableitung zeigt, dass die Funktion ein lokales Minimum bei und ein lokales Maximum bei hat. Die entsprechenden Werte der Funktion sind:
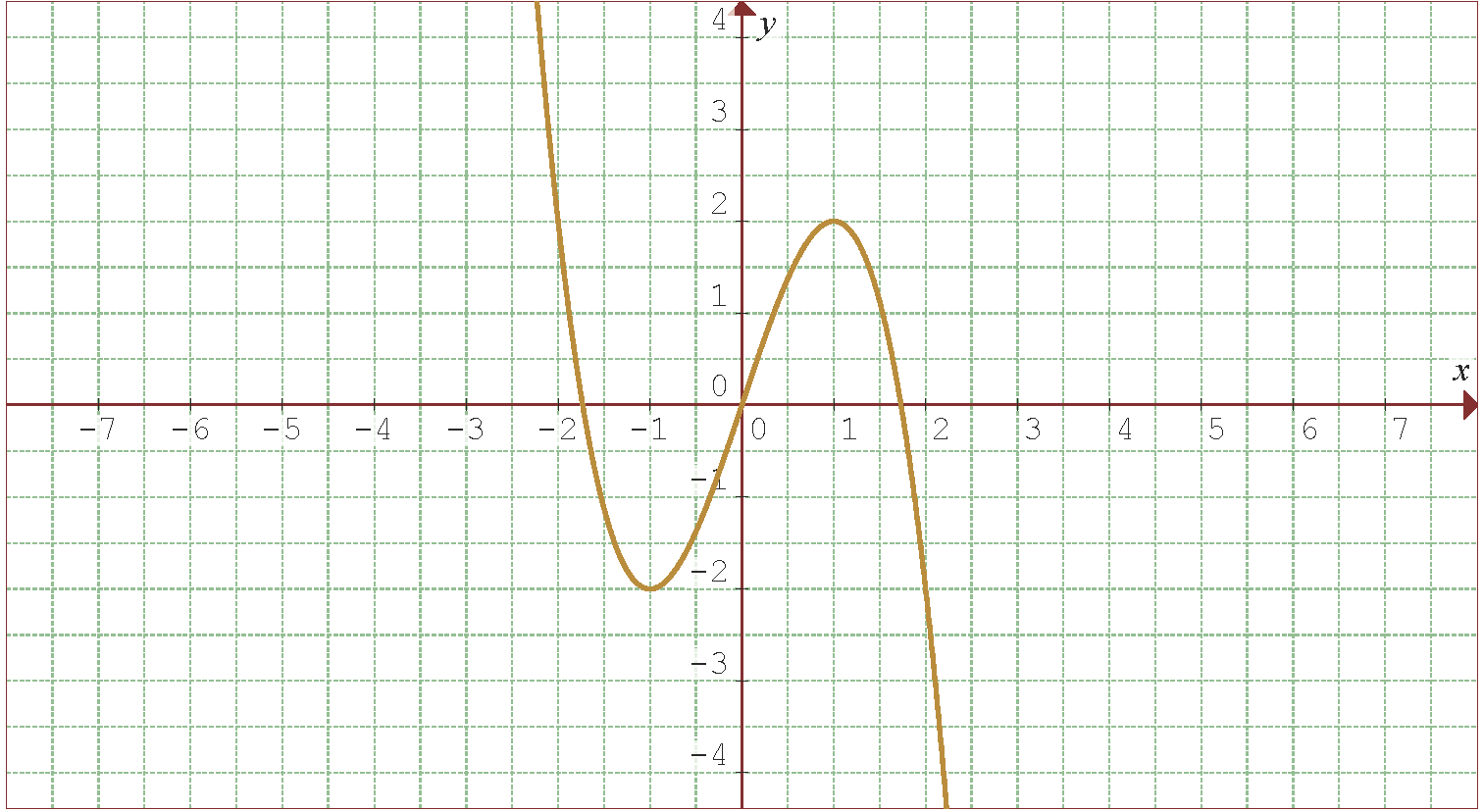
Die folgende Abbildung zeigt den Graphen der Funktion .
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion:
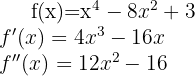
Wir bestimmen nun die kritischen Punkte durch die Lösung (oder Lösungen) der Gleichung , also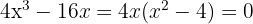 
. Die Lösungen dieser Gleichung lauten 
.
Schließlich werten wir an den kritischen Punkten und bestimmen, ob oder 
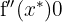
Die 2. Ableitung zeigt, dass die Funktion ein lokales Maximum bei 
und zwei lokale Minima bei 
und 
hat. Die entsprechenden Wert der Funktion sind:
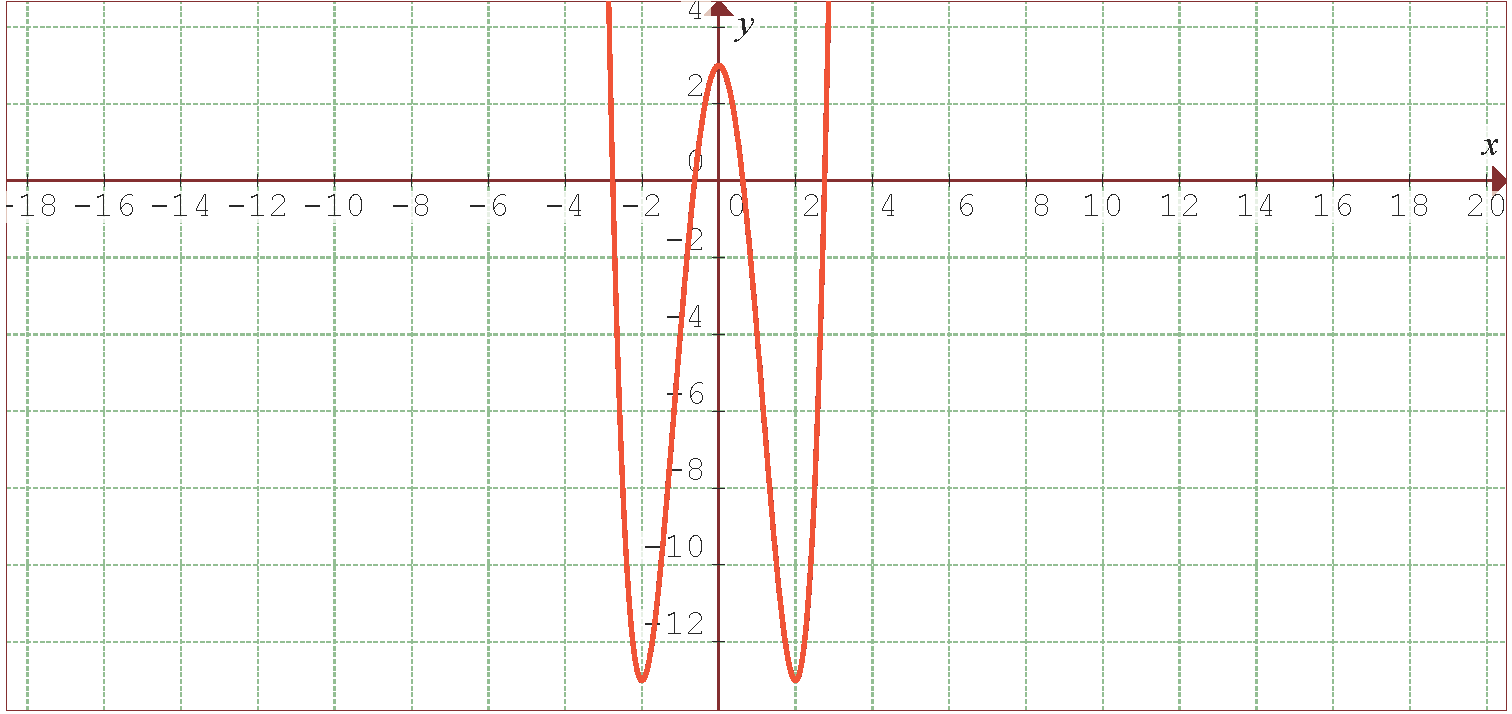
Folgende Abbildung zeigt den Graphen der Funktion .
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion:
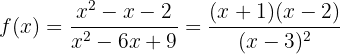
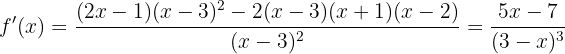
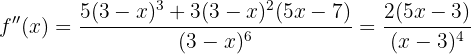
Nun bestimmen wir den kritischen Punkt durch die Lösung der Gleichung , also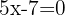 
, deren Lösung 
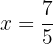ist.
Schließlich werten wir am kritischen Punkt aus und ermitteln, ob oder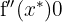
Die 2. Ableitung zeigt, dass die Funktion ein lokales Minimum bei 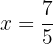hat. Der entsprechende Wert der Funktion ist:
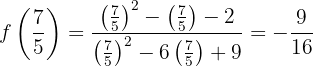
Folgende Abbildung zeigt den Graphen der Funktion .
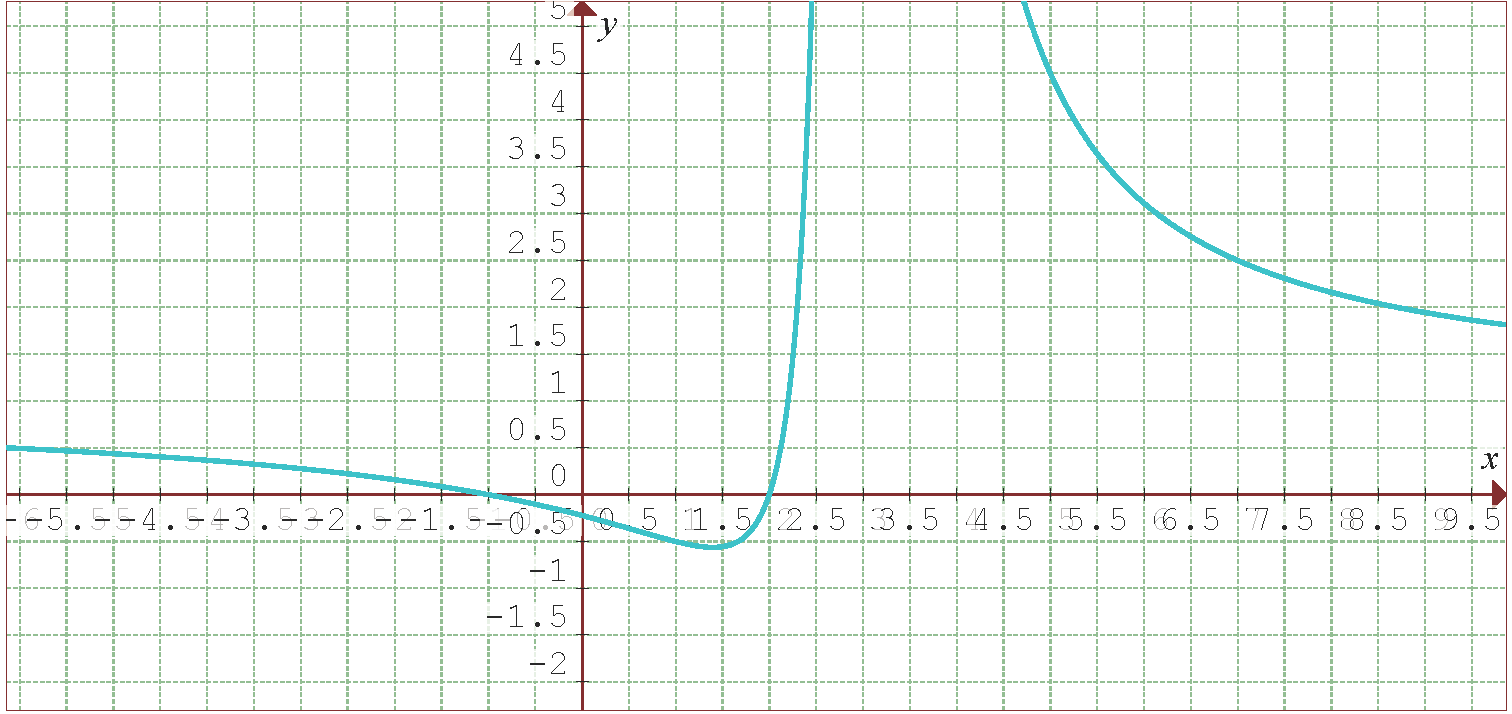
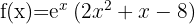
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion:
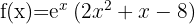
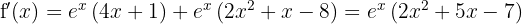
Nun bestimmen wir die kritischen Punkte durch die Lösung (oder Lösungen) der Gleichung , also 
. Die Lösungen dieser Gleichungen sind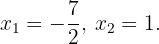 
.
Schließlich werten wir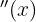 
an den kritischen Punkten aus und ermitteln, ob oder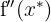
Die 2. Ableitung zeigt, dass die Funktion ein lokales Maximus bei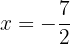 
und ein lokales Minimum bei hat. Die entsprechenden Werte der Funktion sind:
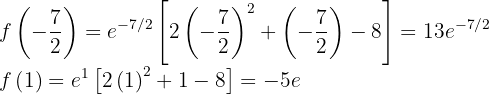
Folgende Abbildung zeigt den Graphen der Funktion .
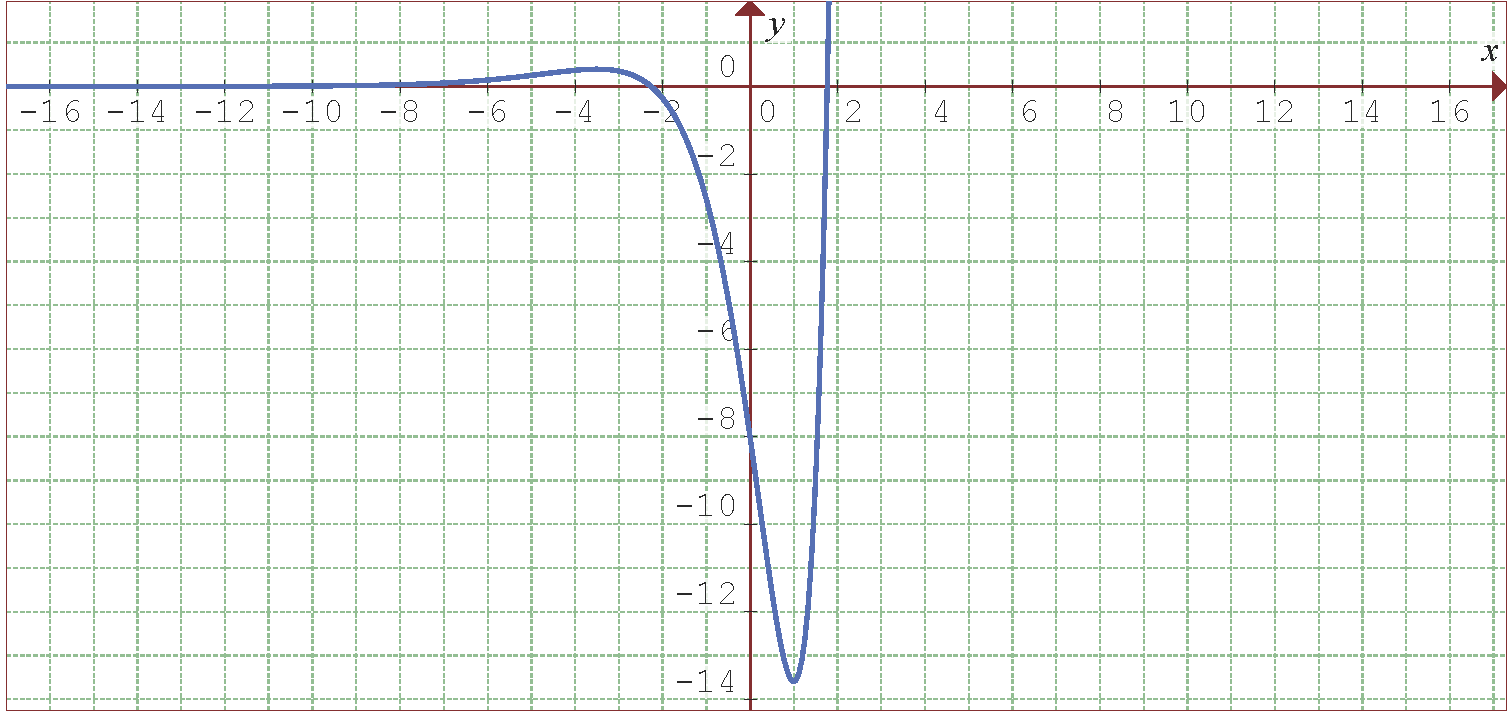
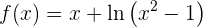
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion:
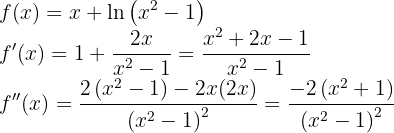
Nun bestimmen wir die kritischen Punkte durch die Lösung (oder Lösungen) der Gleichung
, es decir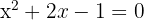
. Die Lösungen dieser Gleichung sind 
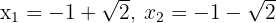. Da die Definitionsmenge der Gleichung 
ist, bedeutet das 
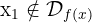
(dies liegt daran, dass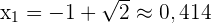 
). Der einzige kritische Punkt, den es zu beachten gilt, ist daher 
.
Schließlich werten wir am kritischen Punkt aus und ermitteln, ob oder 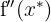ein lokales Maximum bei 
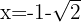hat. Der entsprechende Wert der Funktion ist:
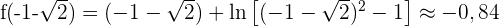
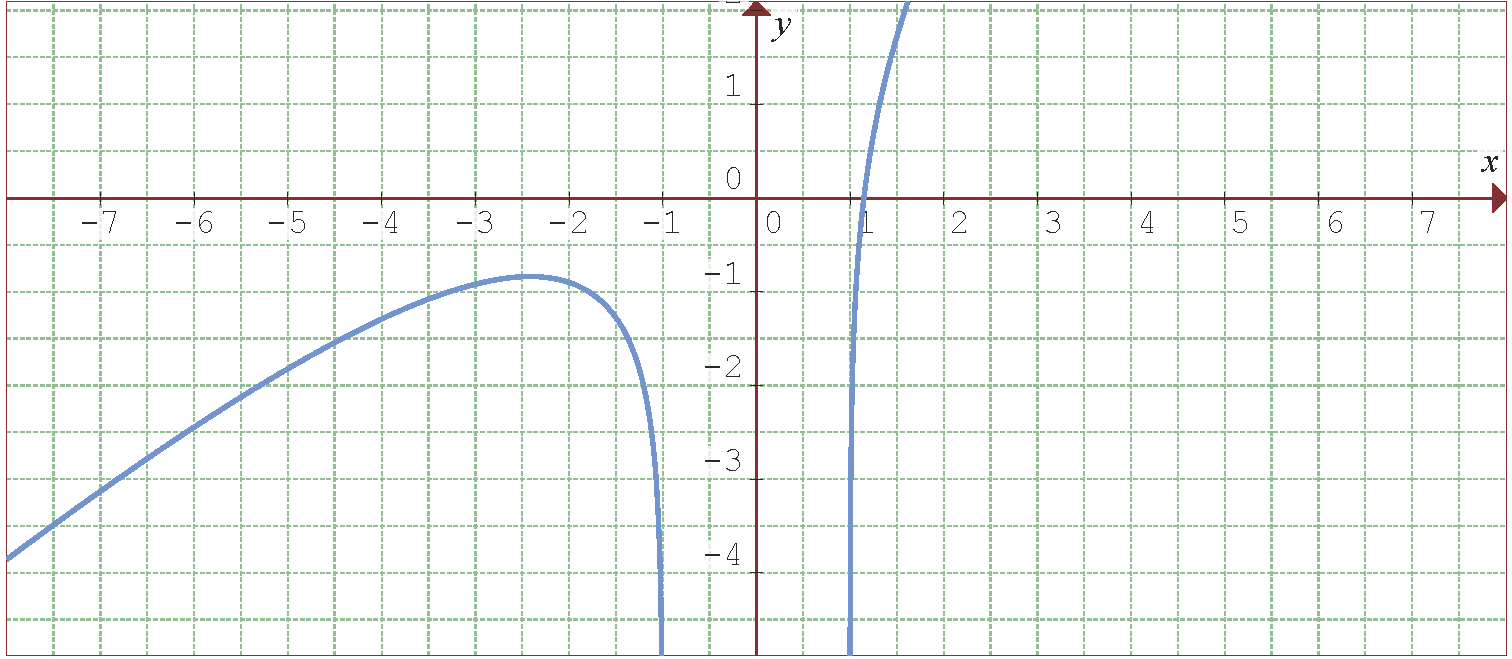
Folgende Abbildung zeigt den Graphen der Funktion .
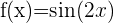
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion:
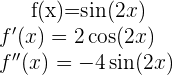
Nun bestimmen wir die kritischen Punkte durch die Lösung (oder Lösungen) der Gleichung , also 
. Hierfür sei 
. Wir erhalten also 
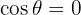, deren Lösungen gegeben sind durch:
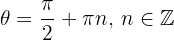
Wenn wir dann zur ursprünglichen Variablen zurückkehren, ergibt sich, dass die kritischen Punkte gegeben sind durch:
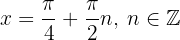
Nun werten wir an den kritischen Punkten aus und ermitteln, ob oder 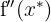(gerade), gilt 
und somit
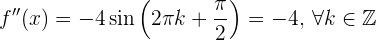
Wenn 
(ungerade), gilt 
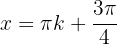
und somit
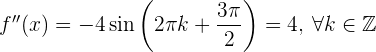
Die 2. Ableitung zeigt, dass die Funktion lokale Maxima bei 
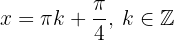und lokale Minima bei 
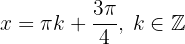hat.
Die entsprechenden Werte für die Funktion sind:
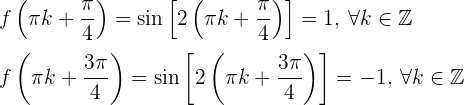
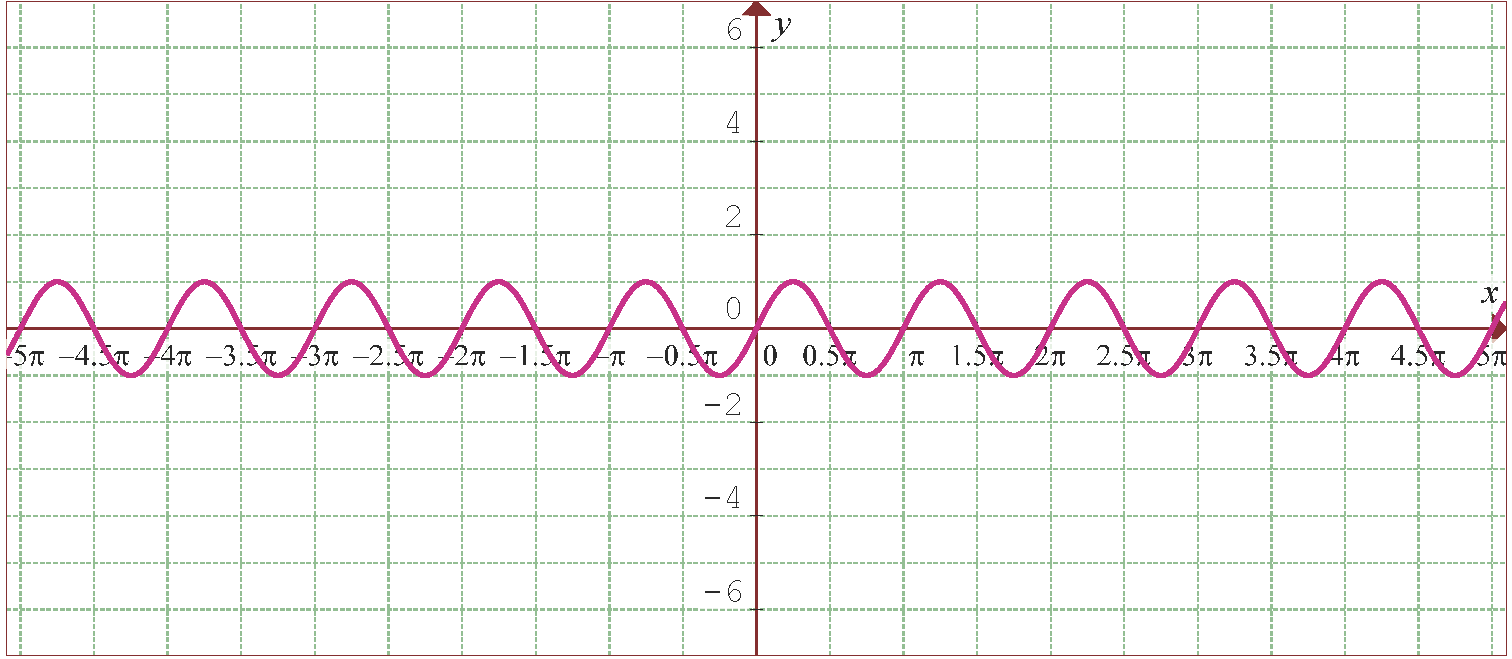
Folgende Abbildung zeigt den Graphen der Funktion .
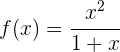
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion:
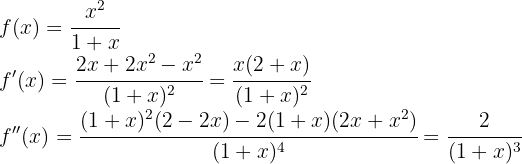
Nun ermittlen wir die kritischen Punkte durch die Lösung (oder Lösungen) der Gleichung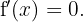 
Wir gehen wie folgt vor
Die Lösungen dieser Gleichung sind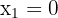 
und 
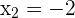. Somit haben wir nur zwei kritische Punkte
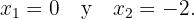
Schließlich werten wir am kritischen Punkt aus und ermitteln, ob oder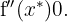 
Die 2. Ableitung zeigt, dass die Funktion ein lokales Minimum bei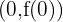 
hat, also am Punkt
Wir kommen nun zum zweiten kritischen Punkt:
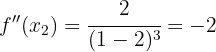ein lokales Maximum bei 
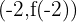hat, also am Punkt 
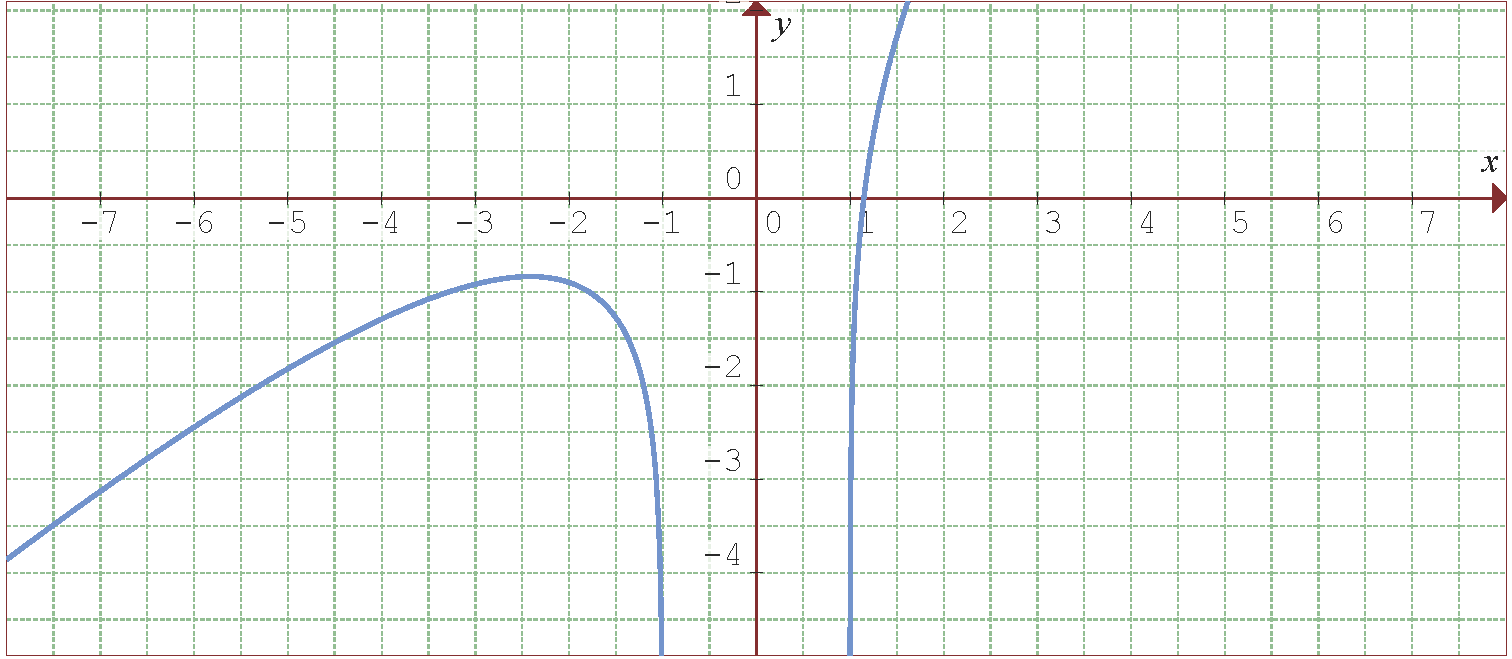
Folgende Abbildung zeigt den Graphen der Funktion .
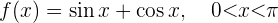
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion: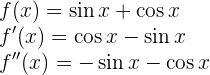
Nun ermitteln wir die kritischen Punkte durch die Lösung (oder Lösungen) der Gleichung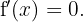
Wir erhalten
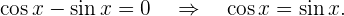
Die Lösungen dieser Gleichungen, für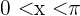 
, sind 
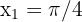und 
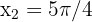. Somit haben wir nur zwei kritische Punkte
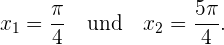
Schließlich bewerten wir am kritischen Punkt und ermitteln, ob oder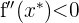 
.
Wir erhalten
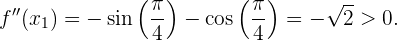
Die 2. Ableitung zeigt, dass die Funktion ein lokales Maximum bei 
hat. Also am Punkt
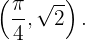
Nun sehen wir und den 2. kritischen Punkt an:
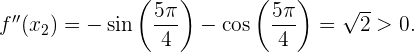
Die 2. Ableitung zeigt, dass die Funktion ein lokales Minimum bei 
hat, also am Punkt
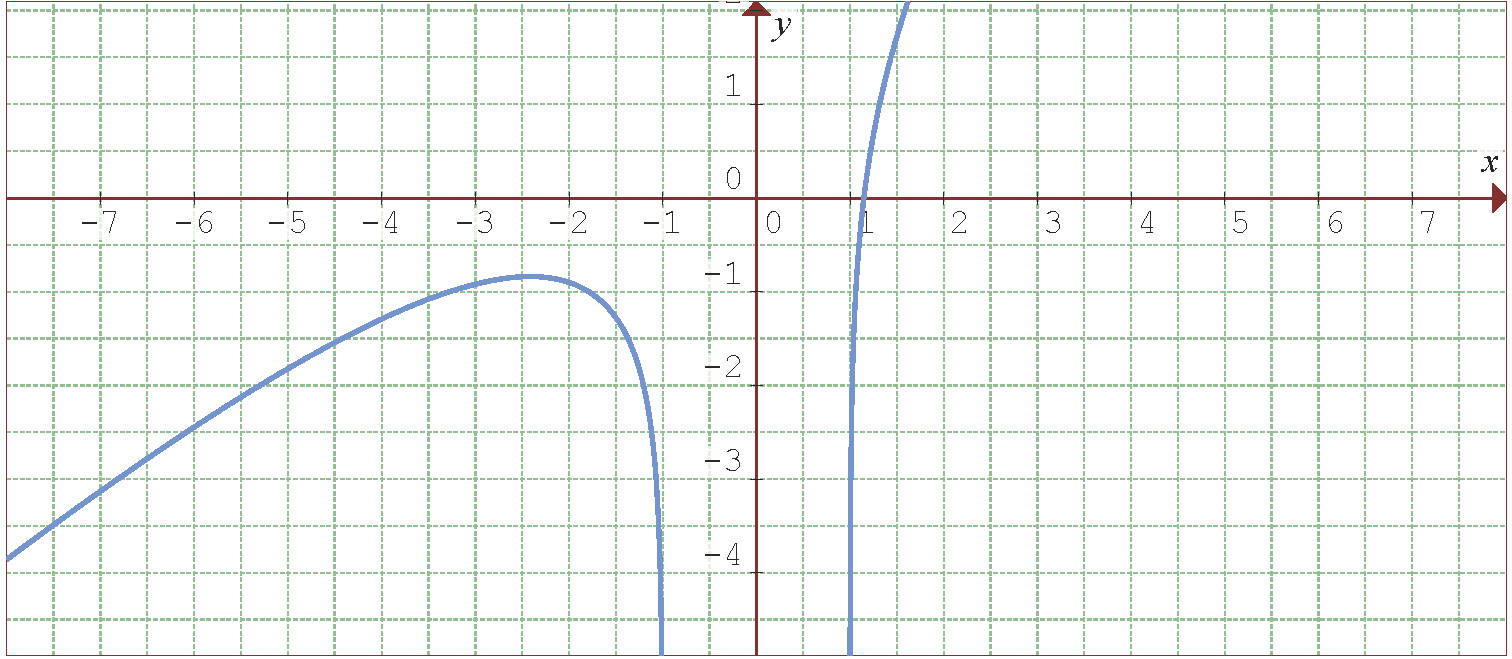
Folgende Abbildung zeigt den Graphen der Funktion .
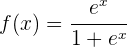
Wir beginnen mit der Ermittlung der 1. und 2. Ableitung der gegebenen Funktion: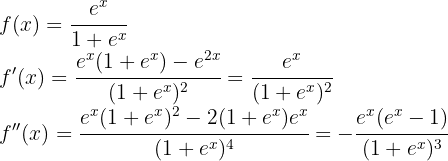
Wir bestimmen nun die kritischen Punkte durch die Lösung (oder Lösungen) der Gleichung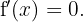
Wir erhalten
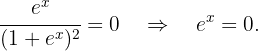
Die Lösung für diese Gleichung ist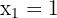 
. Wir haben also nur einen einzigen kritischen Punkt
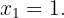
Schließlich werten wir am kritischen Punkt aus und ermitteln, ob oder 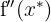ein lokales Maximum bei 
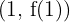hat, also am Punkt
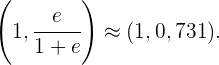
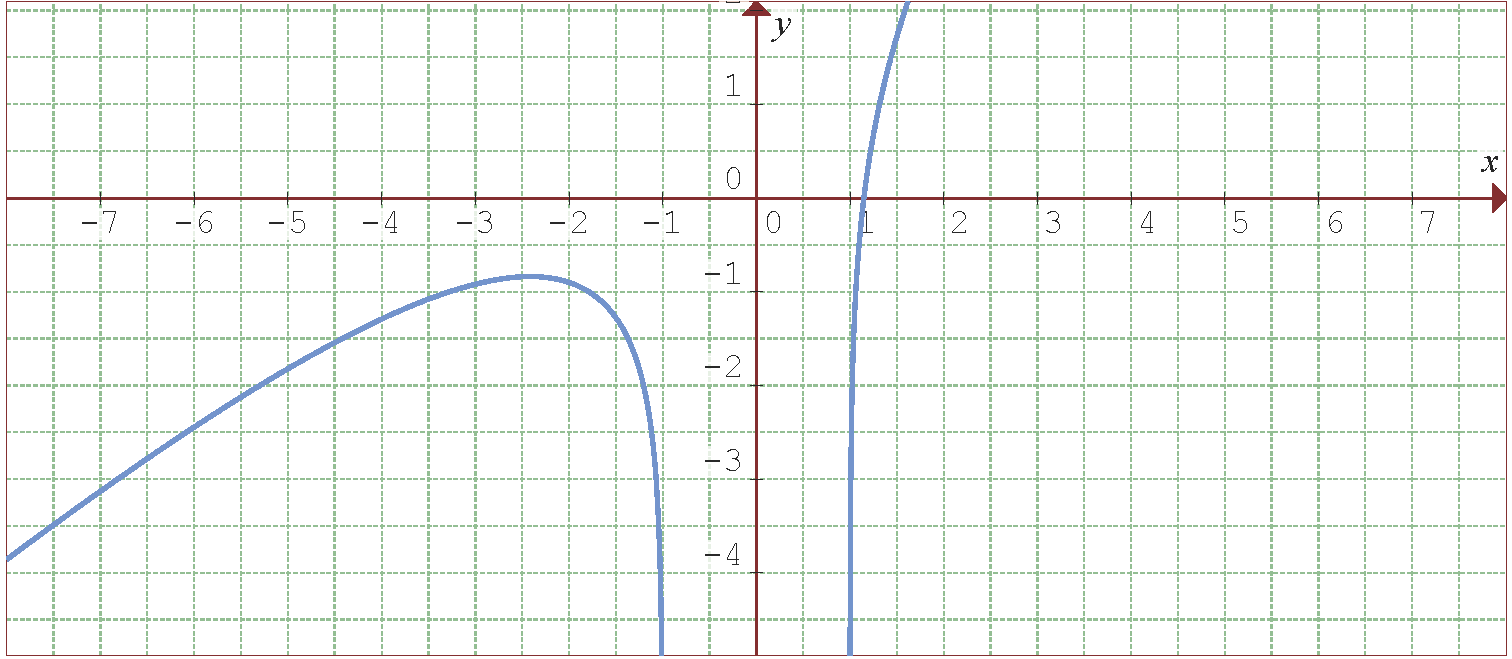
Folgende Abbildung zeigt den Graphen der Funktion .
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
