Zum Verständnis einer mathematischen Funktion gehört viel mehr als nur die Auswertung für verschiedene Eingabewerte. Um ein vollständiges Bild zu erhalten, müssen drei wichtige Aspekte analysiert werden: die Definitionsmenge, die Zielmenge und die grafische Darstellung der Funktion.
Definitionsmenge: Die Menge aller Eingabewerte (Werte von xx), für die die Funktion definiert ist. Bei der Bestimmung der Definitionsmenge müssen Einschränkungen wie Divisionen durch Null oder sogar Wurzeln negativer Zahlen mit geradem Wurzelexponenten berücksichtigt werden.
Zielmenge: Sie ist die Menge der Werte, die die Funktion als Ergebnis annehmen kann (Werte von yy). Die Suche nach der Zielmenge erfordert ein Verständnis des Gesamtverhaltens der Funktion und stützt sich häufig auf ihren Graphen oder algebraische Methoden.
Graph: Die Darstellung einer Funktion in der kartesischen Ebene ermöglicht es, ihr Verhalten deutlich zu visualisieren: Zunahmen, Abnahmen, Maxima, Minima, Symmetrien und besondere Punkte.
In diesem Artikel stellen wir dir Schritt-für-Schritt-Übungen vor, die dir dabei helfen werden, die Definitionsmenge und die Zielmenge verschiedener Funktionen zu identifizieren und ihre Graphen auf begründete Weise darzustellen. Diese Analyse ist für die Vertiefung fortgeschrittener Themen in der Infinitesimalrechnung und für die Anwendung von Funktionen in realen Kontexten unerlässlich.
Aufgaben
Löse die folgenden Aufgaben, indem du das tust, was in jedem Fall vorgegeben ist:
Ermittle die Definitionsmenge und die Zielmenge der folgenden abschnittsweise definierten Funktionen und stelle sie grafisch dar.
a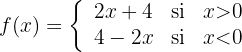 
b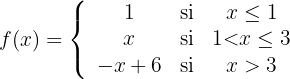 
c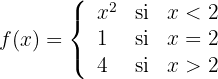 
a Wir beginnen mit dem Graphen der Funktion (sie ist bei 0 nicht definiert)
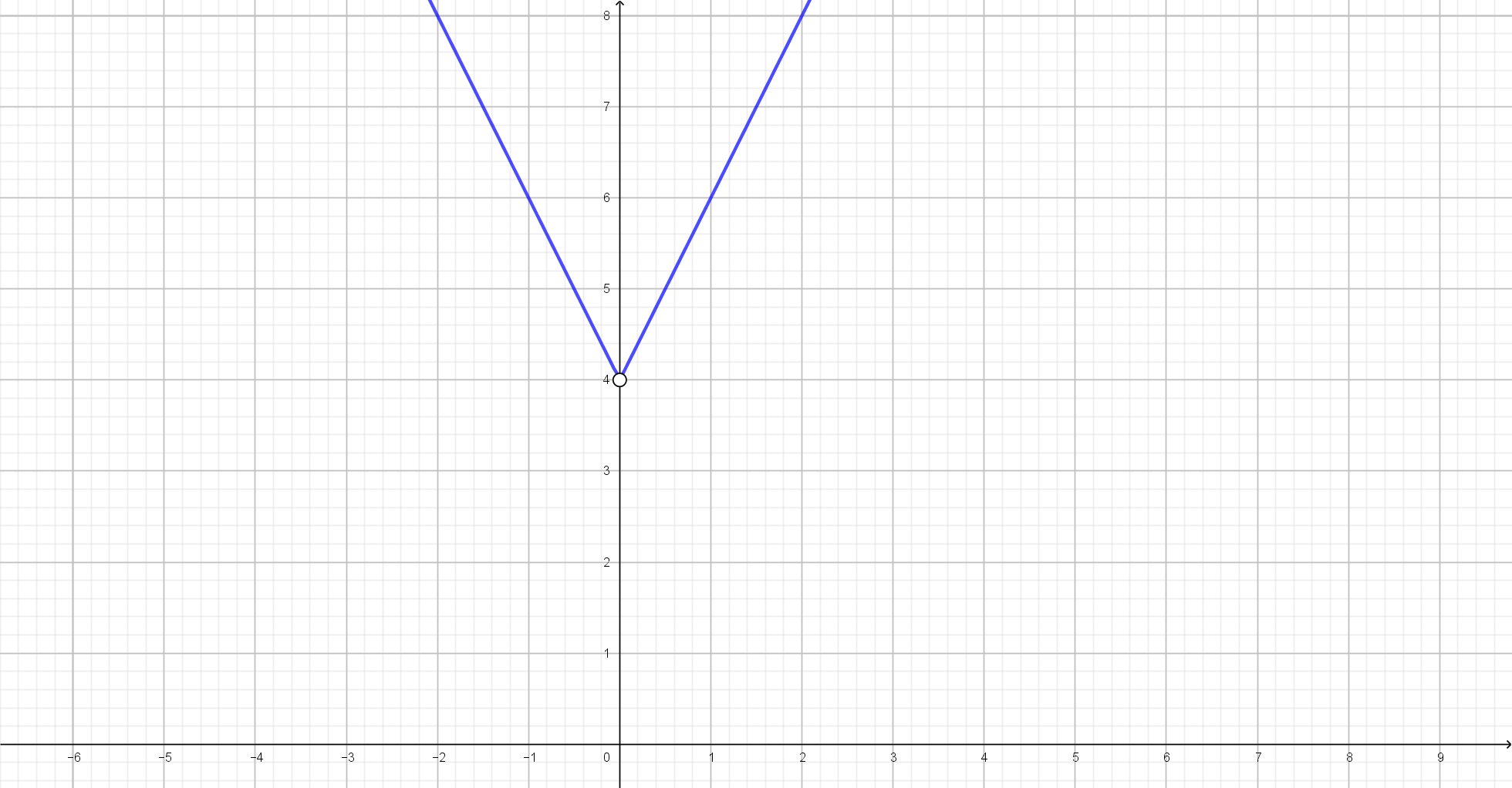
Anhand des Graphen stellen wir fest
Definitionsmenge: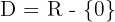 
Zielmenge: 
b Graph:
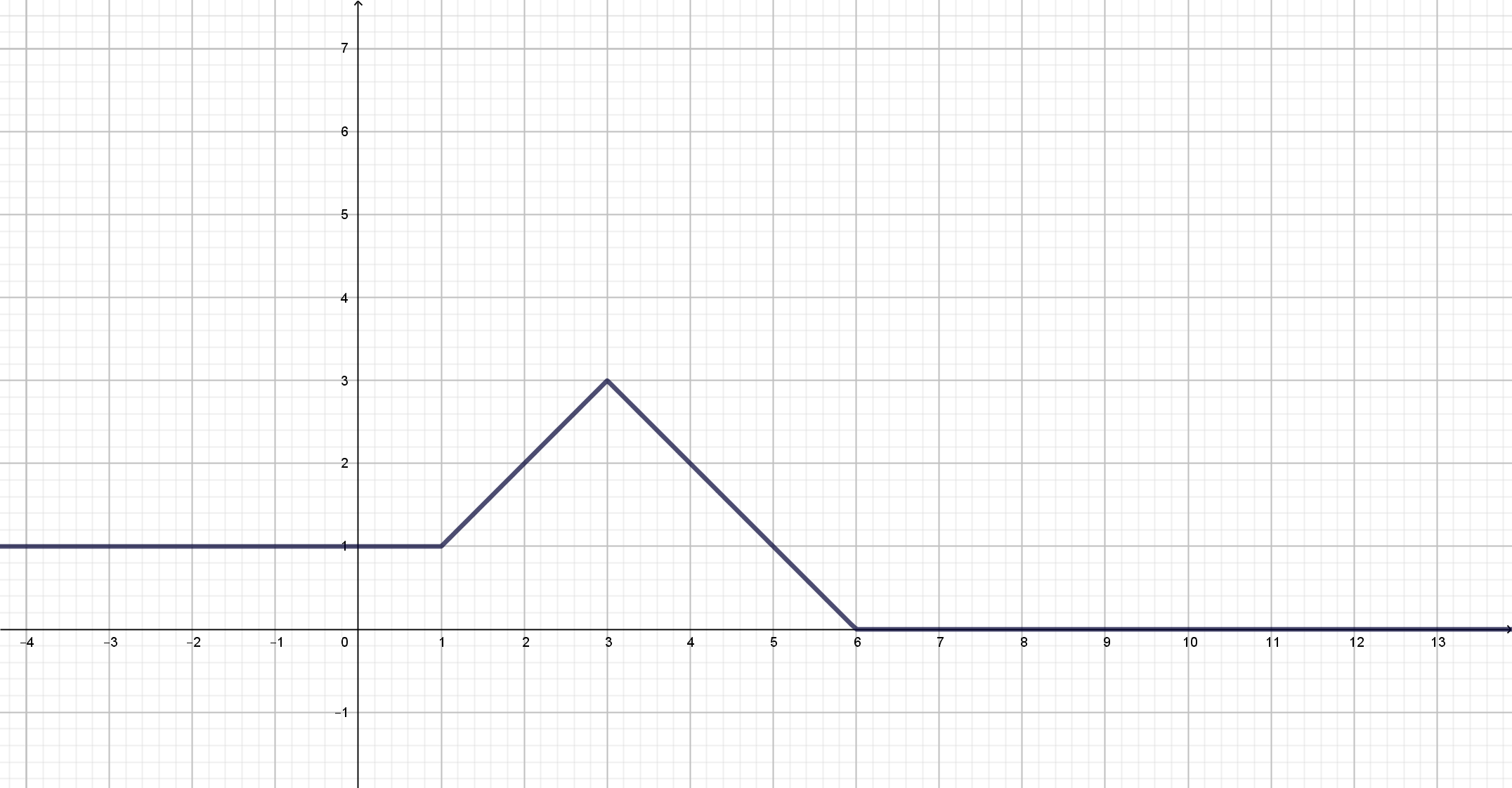
Wir erhalten
Definitionsmenge: 
Zielmenge: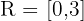 
c Wir sehen, dass der Graph innerhalb der reellen Zahlen definiert ist, allerdings nicht stetig ist
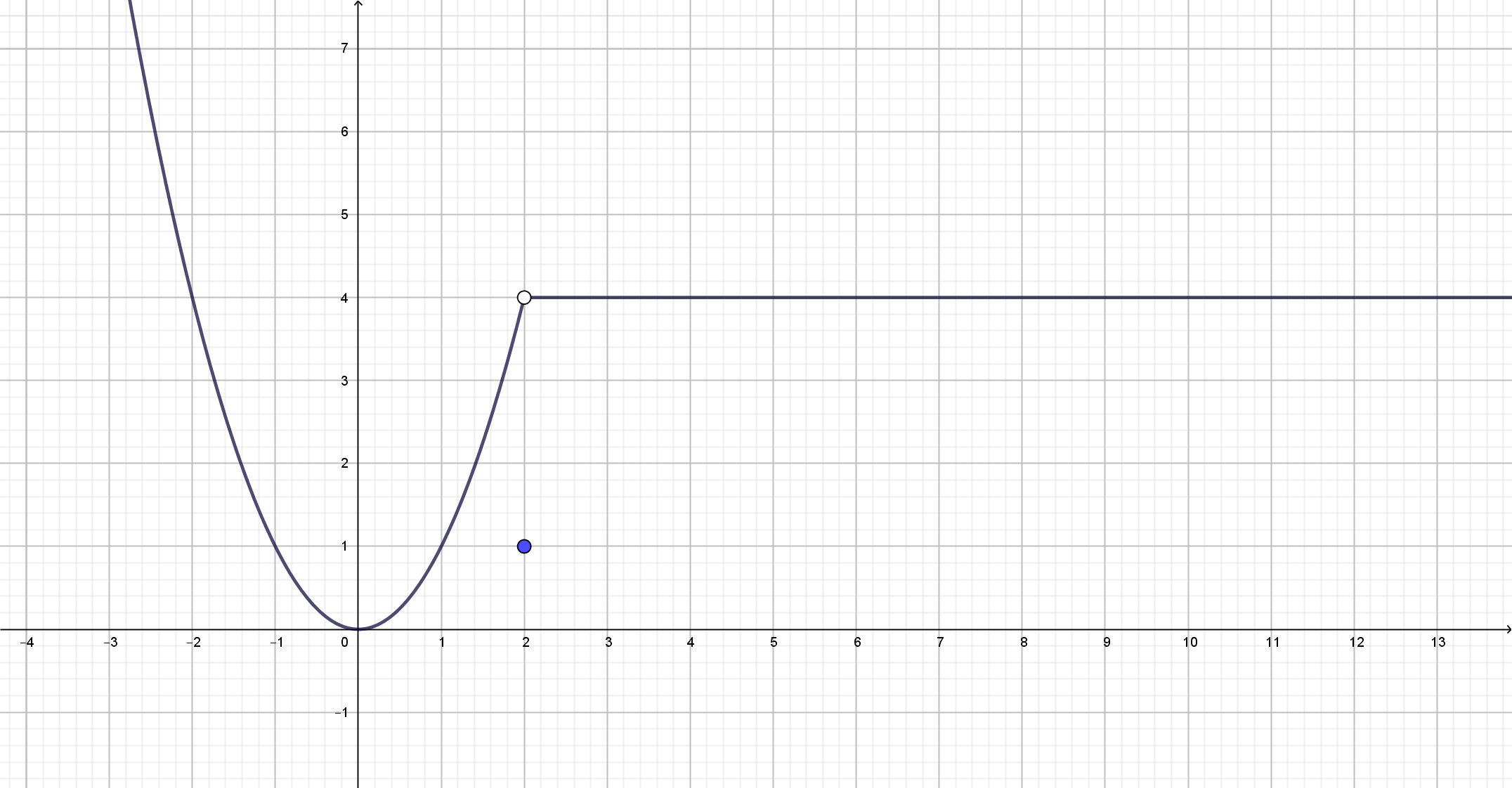
Der Graph zeigt uns
Definitionsmenge:
Zielmenge: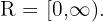 
Ermittle die Definitionsmenge und die Zielmenge der folgenden Betragsfunktionen und stelle sie grafisch dar:
a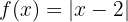
b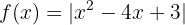
c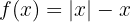
a :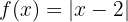
Wir setzen die Funktion ohne den Betrag gleich 0 und berechnen ihre Nullstellen.
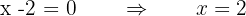
Wir bilden Intervalle mit den Nullstellen und werten das Vorzeichen der einzelnen Intervalle aus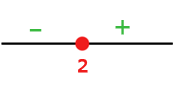
Wir definieren die Funktion abschnittsweise, wobei zu berücksichtigen ist, dass auf den Intervallen, in denen 
negativ ist, sich das Vorzeichen der Funktion ändert
Zielmenge :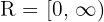 
b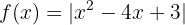
Wir setzen die Funktion ohne den Betrag gleich 0 und berechnen ihre Nullstellen.
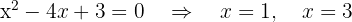
Wir bilden Intervalle mit den Nullstellen und werten das Vorzeichen der einzelnen Intervalle aus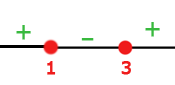
Wir definieren die Funktion abschnittsweise, wobei zu berücksichtigen ist, dass auf den Intervallen, in denen negativ ist, sich das Vorzeichen der Funktion ändert
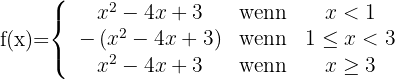
Wir stellen die resultierende Funktion grafisch dar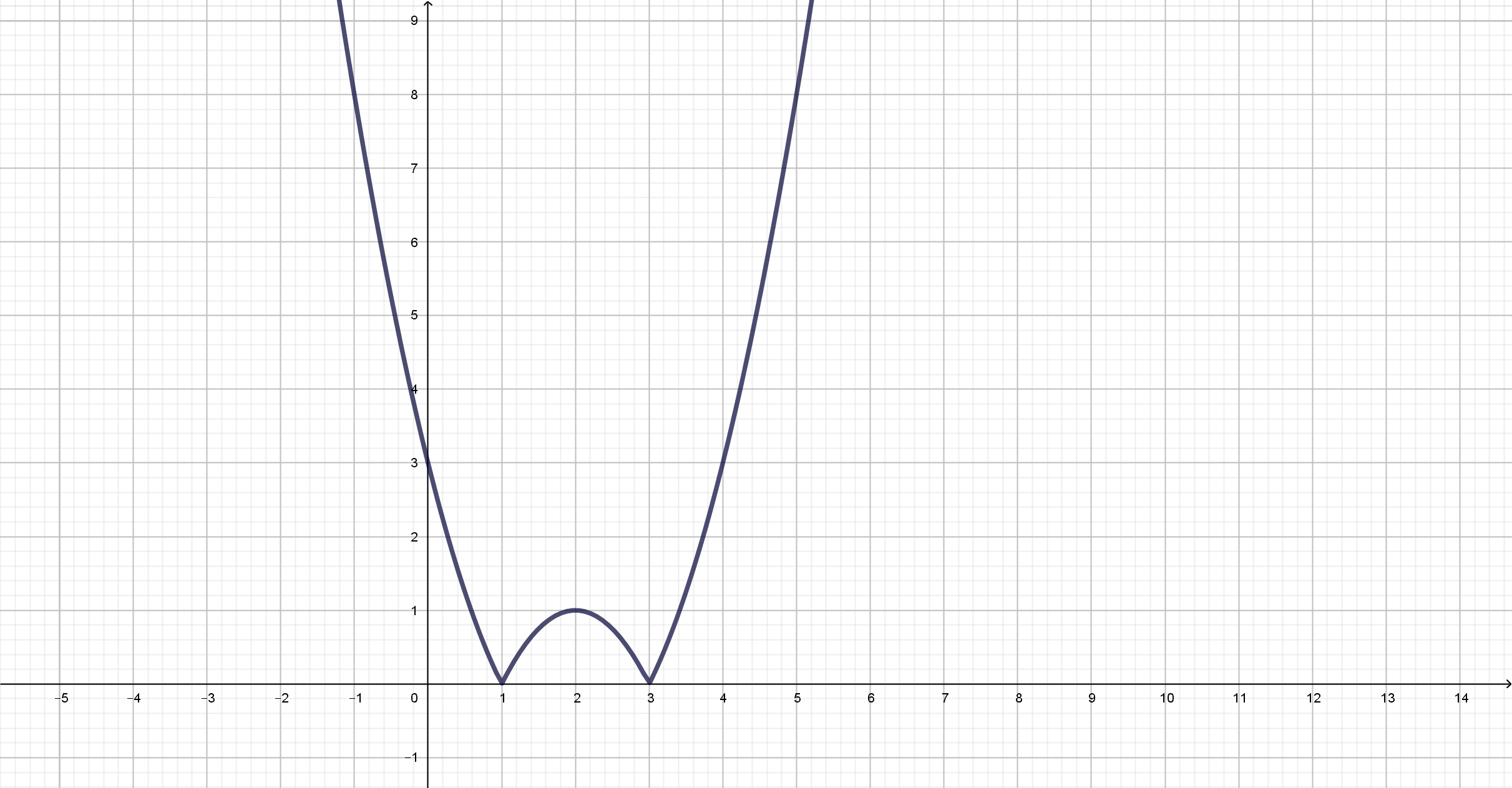
Und somit
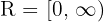
c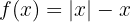
Wir setzen die Funktion ohne den Betrag gleich 0 und berechnen ihre Nullstellen.
Wir bilden Intervalle mit den Nullstellen und werten das Vorzeichen der einzelnen Intervalle aus:
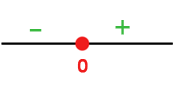
Wir definieren die Funktion abschnittsweise. Dabei ist zu beachten, dass sich in den Intervallen, in denen negativ ist, das Vorzeichen der Funktion ändert:
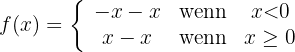
Das bedeutet vereinfacht:
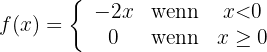
Wir stellen die resultierende Funktion grafisch dar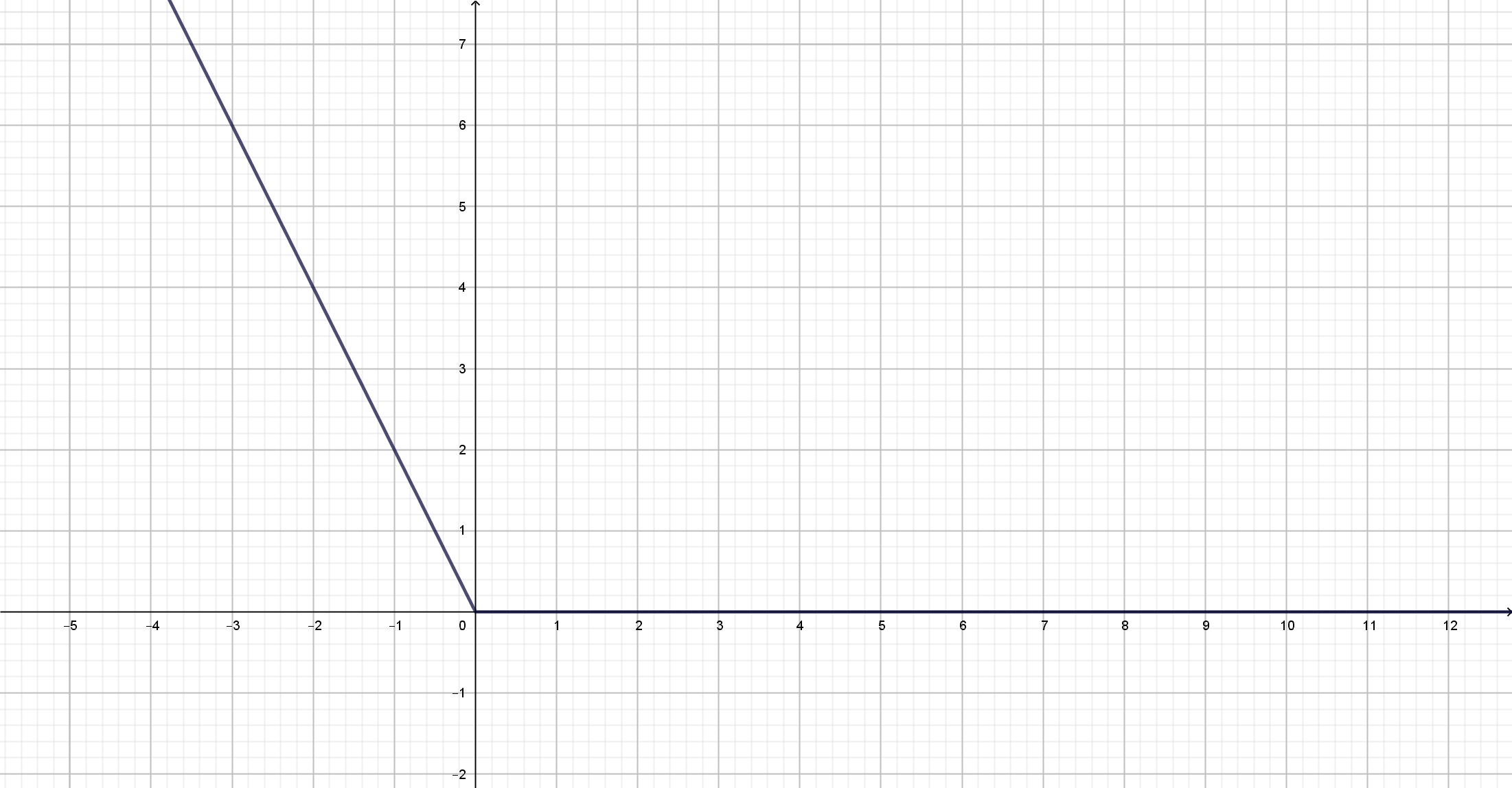
also:
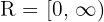
Stelle die Ganzteilfunktionen von grafisch dar:
a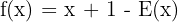 
b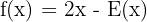
a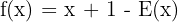
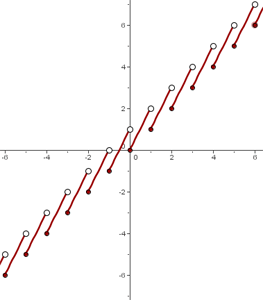
Zunächst müssen wir ein paar Punkte tabellarisch darstellen und dann den Graphen zeichnen
|  |
|---|---|
| 0 | 1 |
| 0,5 | 1,5 |
| 0,9 | 1,9 |
| 1 | 1 |
| 1,5 | 1,5 |
| 1,9 | 1,9 |
Graph:
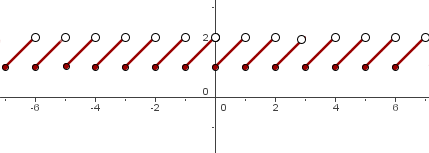
b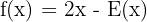
Stelle die rationalen Funktionen grafisch dar und bestimme ihren Mittelpunkt
a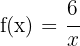 
b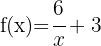 
c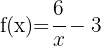 
d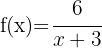
e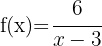 
f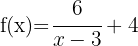 
g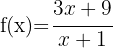 
a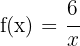
Hyperbel
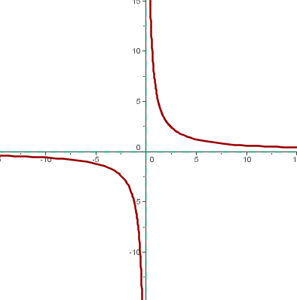
Der Mittelpunkt der Hyperbel ist:(0, 0)
b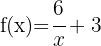
Man bedenke, dass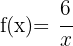 
um 3 Einheiten nach oben verschoben ist, also
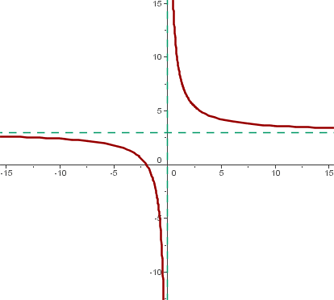
Somit lautet der Mittelpunkt der Hyperbel: (0, 3)
c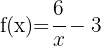
In diesem Fall ist 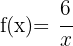um 3 Einheiten nach unten verschoben, also
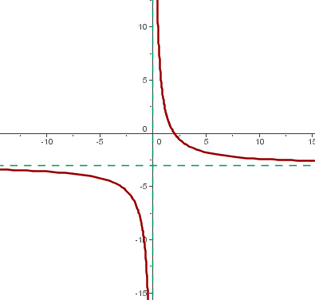
Somit lautet der Mittelpunkt der Hyperbel: (0, -3)
d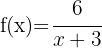
In diesem Fall wird 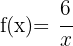um 3 Einheiten nach links verschoben
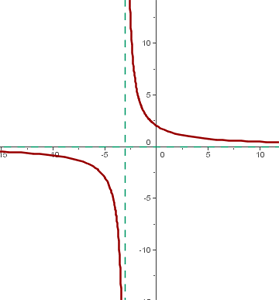
Der Mittelpunkt der Hyperbel ist: (−3, 0)
e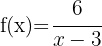
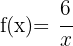wird um 3 Einheiten nach rechts verschoben. Somit
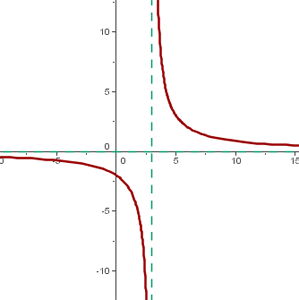
Der Mittelpunkt der Hyperbel ist: (3, 0)
f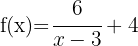
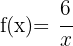wird um 3 Einheiten nach rechts und um 4 Einheiten nach oben verschoben
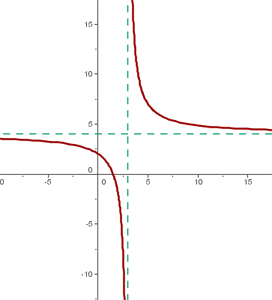
Der Mittelpunkt der Hyperbel ist: (3, 4)
g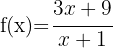
Wir stellen fest, dass
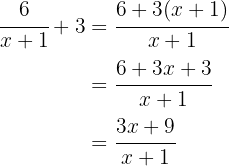
Das heißt
,
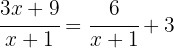und von hier aus ist es einfacher zu sehen, dass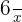 
um 1 Einheit nach links und um 3 Einheiten nach oben verschoben ist.
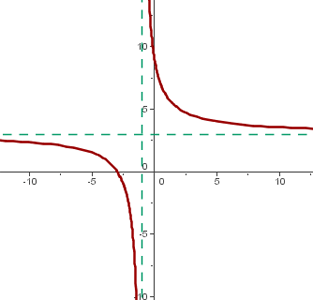
Der Mittelpunkt der Hyperbel ist: (−1, 3)
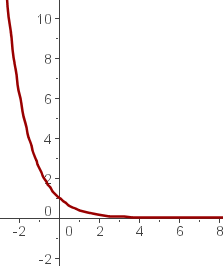
Stelle die Exponentialfunktionen grafisch dar:
a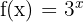 
b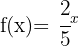
a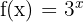
Wir beachten:
| |
|---|---|
| -3 | 1/27 |
| -2; | 1/9 |
| -1 | 1/3 |
| 0 | 1 |
| 1 | 3 |
| 2 | 9 |
| 3 | 27 |
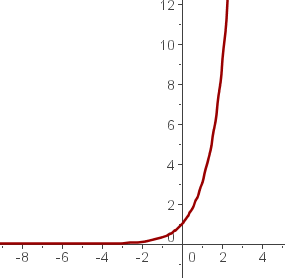
b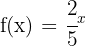
Wir stellen fest, dass
und erstellen folgende Tabelle
| |
|---|---|
| −3 | 15,625 |
| −2 | 6,25 |
| −1 | 2,5 |
| 0 | 1 |
| 1 | 0,4 |
| 2 | 0,16 |
| 3 | 0,064 |
Stelle die Exponentialfunktionen grafisch dar:
a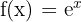
b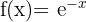
a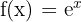
Wir beachten:
| |
|---|---|
| -3 | 1/27 |
| -2; | 1/9 |
| -1 | 1/3 |
| 0 | 1 |
| 1 | 3 |
| 2 | 9 |
| 3 | 27 |
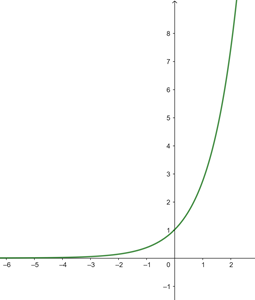
b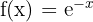
Wir stellen fest, dass
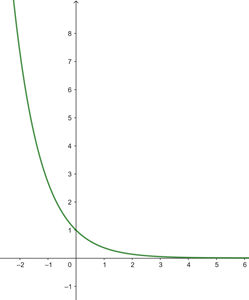
wir erstellen folgende Tabelle
| |
|---|---|
| −3 | 15,625 |
| −2 | 6,25 |
| −1 | 2,5 |
| 0 | 1 |
| 1 | 0,4 |
| 2 | 0,16 |
| 3 | 0,064 |
Stelle die Logarithmusfunktionen grafisch dar:
a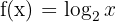
b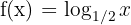
a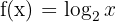
Wir stellen einige Punkte tabellarisch dar, um zu sehen, wie sie sich verhält
| |
|---|---|
| 1/8 | -3 |
| 1/4 | -2 |
| 1/2 | -1 |
| 1 | 0 |
| 2; | 1 |
| 4 | 2 |
| 8 | 3 |
Grafisch dargestellt:
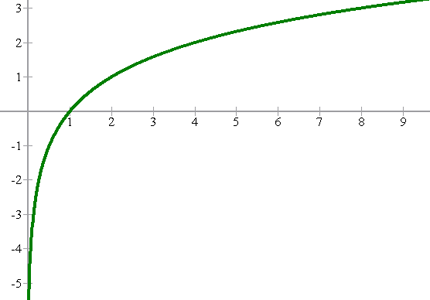
b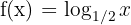
Wir erhalten folgenden Graphen
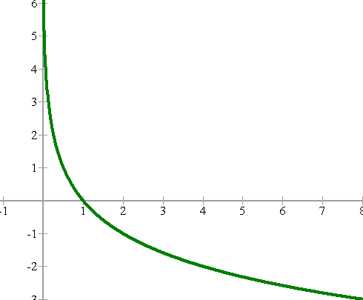
Wie in der vorangegangenen Aufgabe könnte man sie in Tabellenform darstellen, um zu sehen, wie sie sich verhält.
Stelle folgende Logarithmusfunktionen grafisch dar:
a
b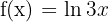
a
wir stellen einige Punkte tabellarisch dar, um zu sehen, wie sie sich verhält
| |
|---|---|
| 1/8 | -3 |
| 1/4 | -2 |
| 1/2 | -1 |
| 1 | 0 |
| 2; | 1 |
| 4 | 2 |
| 8 | 3 |
Grafisch dargestellt:
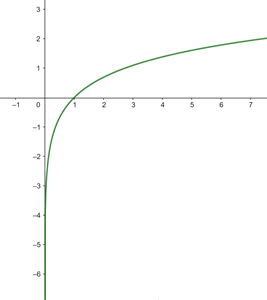
b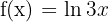
Grafisch dargestellt:
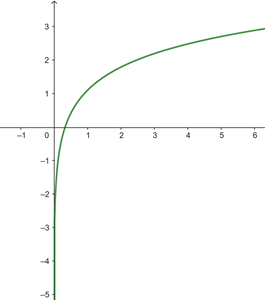
Wie in der vorangegangenen Aufgabe könnte man sie in Tabellenform darstellen, um zu sehen, wie sie sich verhält.
Stelle die folgenden trigonometrischen Funktionen grafisch dar:
a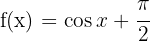
b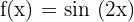
a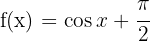
| 0 | 0 |
|---|---|
| π/4 | -0,7 |
| π/2 | -1 |
| 3π/4 | -0,7 |
| π | 0 |
| 5π/4 | 0,7 |
| 3π/2 | 1 |
| 7π/4 | 0,7; |
| 2π | 0 |
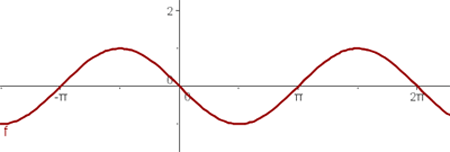
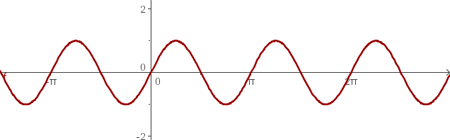
b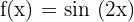
| 0 | 0 |
|---|---|
| π/4 | 1 |
| π/2 | 0 |
| 3π/4 | -1 |
| π | 0 |
| 5π/4 | 1 |
| 3π/2 | 0 |
| 7π/4 | -1 |
| 2π | 0 |
Stelle die folgenden trigonometrischen Funktionen grafisch dar:
a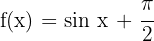
b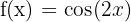
a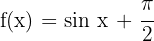
| 0 | 0 |
|---|---|
| π/4 | -0,7 |
| π/2 | -1 |
| 3π/4 | -0,7 |
| π | 0 |
| 5π/4 | 0,7 |
| 3π/2 | 1 |
| 7π/4 | 0,7; |
| 2π | 0 |
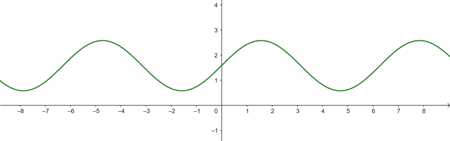
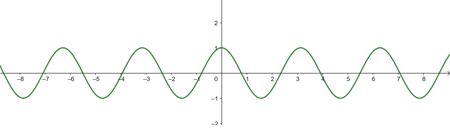
b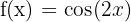
| 0 | 0 |
|---|---|
| π/4 | 1 |
| π/2 | 0 |
| 3π/4 | -1 |
| π | 0 |
| 5π/4 | 1 |
| 3π/2 | 0 |
| 7π/4 | -1 |
| 2π | 0 |
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
