
Wie man die Umkehrfunktion bestimmen kann
Die Umkehrfunktion von  ist definiert als die Funktion
ist definiert als die Funktion  und somit
und somit 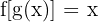 und
und 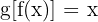 . Daher können wir sie ausgehend von
. Daher können wir sie ausgehend von  bestimmen.
bestimmen.
Ebenso wird die Umkehrfunktion von  in der Regel als
in der Regel als  bezeichet (beachte, dass sich
bezeichet (beachte, dass sich  im vorherigen Ausdruck nicht auf einen negativen Exponenten bezieht, sondern nur angibt, dass es sich um eine Umkehrfunktion handelt).
im vorherigen Ausdruck nicht auf einen negativen Exponenten bezieht, sondern nur angibt, dass es sich um eine Umkehrfunktion handelt).
Hinweis: Damit eine Funktion  eine Umkehrfunktion hat, ist es im Allgemeinen erforderlich, dass die Funktion eineindeutig (oder bijektiv) ist. Wenn dies nicht der Fall ist, muss der Definitionsbereich eingeschränkt werden.
eine Umkehrfunktion hat, ist es im Allgemeinen erforderlich, dass die Funktion eineindeutig (oder bijektiv) ist. Wenn dies nicht der Fall ist, muss der Definitionsbereich eingeschränkt werden.
Wir beachten, dass eine eineindeutige Funktion eine Funktion ist, die jedem Element der Zielmenge einen anderen Wert in der Wertemenge zuweist. Das heißt, wenn 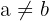 , ist
, ist 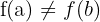 .
.
Vorgehensweise, um die Umkehrfunktion zu bestimmen
1 Ersetze  durch
durch  .
.
2 Bestimme die Variable  . Wir erhalten also einen Ausdruck der Form
. Wir erhalten also einen Ausdruck der Form 
3 Ersetze bei 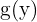 die Variable
die Variable  durch
durch  .
.
4 Und schließlich ändern wir das  auf der linken Seite in
auf der linken Seite in  .
.
Beispiel: Wir betrachten die Funktion 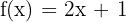 . Um die Umkehrfunktion zu ermitteln, befolgen wir folgende Schritte:
. Um die Umkehrfunktion zu ermitteln, befolgen wir folgende Schritte:
1 Wir substituieren  durch
durch  :
: 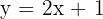 .
.
2 Wir bestimmen  :
:
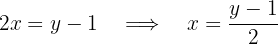 ,
,
wobei 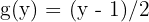 ist
ist
3 Wir tauschen  mit
mit  :
:
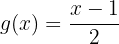
4 Wir ändern das  der linken Seite in
der linken Seite in  :
:
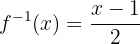
Schließlich prüfen wir, ob die Funktion die Umkehrfunktion der Funktion ist:
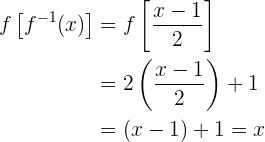
Wir stellen fest, dass  erfüllt ist.
erfüllt ist.
Aufgaben
Ermittle die Umkehrfunktion der folgenden linearen Funktion:
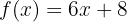
Wir ermitteln die Umkehrfunktion, ohne die einzelnen Schritte anzugeben. Wir haben  und substituieren
und substituieren  durch
durch  :
:
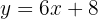
Wir bestimmen  :
:
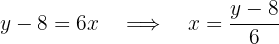
Und schließlich substituieren wir  durch
durch  und
und  durch
durch  :
:
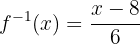 ,
,
welche die Umkehrfunktion ist.
Berechne die Umkehrfunktion der folgenden Funktion

Zunächst substituieren wir  durch
durch  :
:
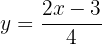
Wir bestimmen  :
:

Das heißt

Und schließlich substituieren wir  durch
durch  und
und  durch
durch  :
:
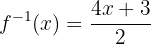 ,
,
welche die Umkehrfunktion ist.
Ermittle die Umkehrfunktion der folgenden Funktion (du musst nicht vereinfachen):
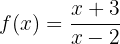
Wir beginnen, indem wir  durch
durch  substituieren :
substituieren :
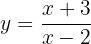
Nun möchten wir  bestimmen. Hierfür multiplizieren wir mit
bestimmen. Hierfür multiplizieren wir mit  :
:

Wir bringen  auf eine Seite der Gleichung und die restlichen Terme auf die andere Seite:
auf eine Seite der Gleichung und die restlichen Terme auf die andere Seite:
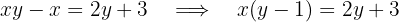
Zuletzt dividieren wir durch 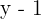 :
:
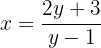
Die Umkehrfunktion ist also
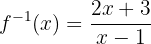
Berechne die Umkehrfunktion der folgenden quadratischen Gleichung
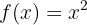
Wir stellen fest, dass  eine eineindeutige Funktion ist (zum Beispiel
eine eineindeutige Funktion ist (zum Beispiel 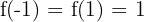 ). Daher hat sie keine Umkehrfunktion im gesamten Definitionsbereich.
). Daher hat sie keine Umkehrfunktion im gesamten Definitionsbereich.
Wenn wir jedoch das Intervall  als Definitionsbereich betrachten, dann ist die Funktion eineindeutig. In diesem Fall erhält man die Umkehrfunktion wie folgt:
als Definitionsbereich betrachten, dann ist die Funktion eineindeutig. In diesem Fall erhält man die Umkehrfunktion wie folgt:

Wir bestimmen  (und unter Verwendung der Tatsache, dass im gesamten beschränkten Definitionsbereich
(und unter Verwendung der Tatsache, dass im gesamten beschränkten Definitionsbereich 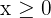 ist):
ist):
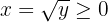
In diesem Fall ist die Umkehrfunktion also
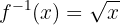
Wenn wir andererseits den Definitionsbereich auf 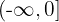 beschränken, erhalten wir die Umkehrfunktion wie folgt:
beschränken, erhalten wir die Umkehrfunktion wie folgt:

Wir bestimmen  (womit
(womit 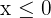 erfüllt ist):
erfüllt ist):
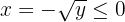
Die Umkehrfunktion ist somit

Dies bedeutet, dass 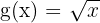 die Umkehrfunktion von
die Umkehrfunktion von  ist. Allerdings nur dann, wenn der Definitionsbereich reelle, positive Zahlen
ist. Allerdings nur dann, wenn der Definitionsbereich reelle, positive Zahlen  sind. Wenn der Definitionsbereich alle reelle Zahlen sind, hat die Funktion keine Umkehrfunktion.
sind. Wenn der Definitionsbereich alle reelle Zahlen sind, hat die Funktion keine Umkehrfunktion.
Ermittle die Umkehrfunktion der folgenden Funktion:
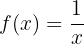
Wir beginnen, indem wir  durch
durch  substituieren:
substituieren:
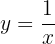
Wir bestimmen  :
:
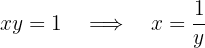
Die Umkehrfunktion ist also
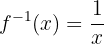
Ermittle die Umkehrfunktion der folgenden Funktion:
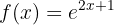
Wir beginnen, indem wir  durch
durch  substituieren:
substituieren:
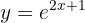
Denk daran, dass der natürliche Logarithmus die folgende Bedingung erfüllt
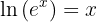
Wir wenden also den natürlichen Logarithmus auf beide Seiten der Gleichung an:
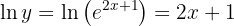
und somit
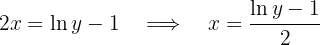
Die Umkehrfunktion ist also
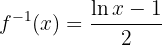
Ermittle die Umkehrfunktion der folgenden Funktion
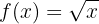
Rationale Funktionen sind eineindeutig. Deshalb haben sie eine Umkehrfunktion:
 ,
,
wobei wir wissen, dass  . Wir quadrieren beide Seiten der Gleichung:
. Wir quadrieren beide Seiten der Gleichung:
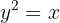
Die Umkehrfunktion ist also
 ,
,
wobei 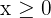 (da wir
(da wir  mit
mit  tauschen, erfüllt
tauschen, erfüllt  schließlich
schließlich 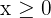 ).
).
Mit anderen Worten: Damit 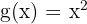 die Umkehrfunktion von
die Umkehrfunktion von  ist, muss gelten, dass
ist, muss gelten, dass  den Definitionsbereich
den Definitionsbereich  hat.
hat.
Ermittle die Umkehrfunktion von

Wir wissen, dass die Kubikwurzelfunktion eineindeutig ist, dass ihr Definitionsbereich alle reellen Zahlen sind, und dass ihre Wertemenge ebenfalls alle reellen Zahlen sind. Daher hat sie eine Umkehrfunktion, deren Definitionsbereich alle reellen Zahlen sind:

Wir nehmen beide Seiten hoch 3:

Das heißt
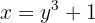
Die Umkehrfunktion ist also
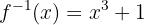
Ermittle die Umkehrfunktion von

Überprüfe außerdem:
a 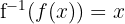
b 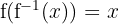
Zunächst ermitteln wir die Umkehrfunktion und substituieren hierfür  durch
durch  :
:

Nun bestimmen wir  :
:

Das heißt
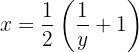
Wir haben  bereits bestimmt. Jedoch vereinfachen wir noch ein wenig::
bereits bestimmt. Jedoch vereinfachen wir noch ein wenig::
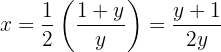
Die Umkehrfunktion ist also

Nun überprüfen wir die gegebenen Aussagen:
a Als Erstes überprüfen wir, ob 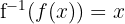 . Hierfür substituieren wir
. Hierfür substituieren wir  durch seinen Wert
durch seinen Wert
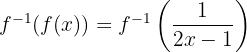
Im Anschluss werten wir  mit der gegebenen Aussage aus
mit der gegebenen Aussage aus
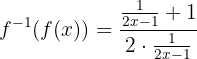
Wir vereinfachen

das heißt
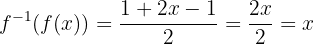
Die erste Beziehung ist also erfüllt.
b Nun überprüfen wir, ob 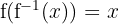 . Wir substituieren
. Wir substituieren  durch seinen Ausdruck:
durch seinen Ausdruck:
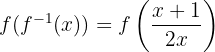
Wir werten  aus:
aus:
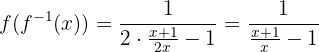
das heißt
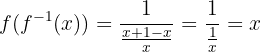
Die zweite Beziehung ist also ebenfalls erfüllt.
Berechne die Umkehrfunktion der folgenden Funktion
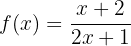
und überprüfe, ob 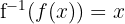 .
.
Wir beginnen mit der Berechnung der Umkehrfunktion. Deshalb substituieren wir  durch
durch  :
:
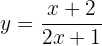
Wir bestimmen nun  und multiplizieren deshalb mit
und multiplizieren deshalb mit  :
:

Im Anschluss bringen wir die Terme mit  auf die linke Seite der Gleichung und die verbleibenen Terme auf die rechte Seite:
auf die linke Seite der Gleichung und die verbleibenen Terme auf die rechte Seite:
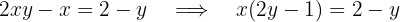
Deshalb
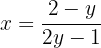
Somit ist die Umkehrfunktion
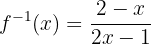
Nun überprüfen wir, ob 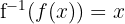 erfüllt ist. Wir substituieren zunächst den Ausdruck
erfüllt ist. Wir substituieren zunächst den Ausdruck  :
:

Wir werten nun die Umkehrfunktion aus:
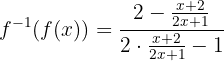
Wir vereinfachen:
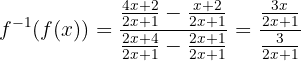
Und somit:

Daher ist die Beziehung erfüllt.
Berechne die Umkehrfunktion der Funktion 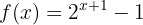
Wir beginnen, indem wir 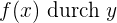 substituieren. Im Anschluss bestimmen wir für
substituieren. Im Anschluss bestimmen wir für  :
:
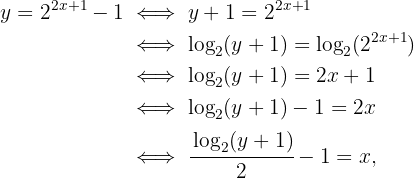
Das heißt:
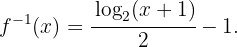
Berechne die Umkehrfunktion der Funktion 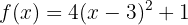 im geeigneten Definitionsbereich.
im geeigneten Definitionsbereich.
Als Erstes stellen wir fest, dass die Funktion injektiv ist. Nämlich 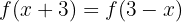 . Somit suchen wir die Umkehrfunktion im Wertebereich
. Somit suchen wir die Umkehrfunktion im Wertebereich  . Wir beginnen, indem wir
. Wir beginnen, indem wir 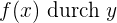 substituieren und
substituieren und  bestimmen:
bestimmen:
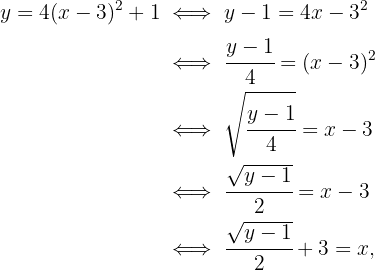
Das heißt
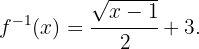
Berechne die Umkehrfunktion der Funktion 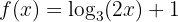
Wir beginnen, indem wir 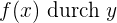 substituieren. Danach bestimmen wir
substituieren. Danach bestimmen wir  :
:
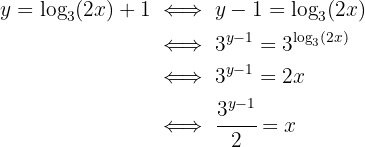
Das heißt
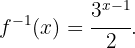
Berechne die Umkehrfunktion der Funktion 
Wir beginnen, indem wir 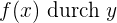 substituieren. Danach bestimmen wir
substituieren. Danach bestimmen wir  :
:
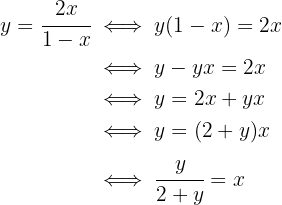
Das heißt:
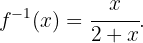
Berechne die Umkehrfunktion der Funktion 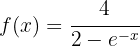
Wir beginnen, indem wir 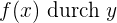 substituieren. Danach bestimmen wir
substituieren. Danach bestimmen wir  :
:
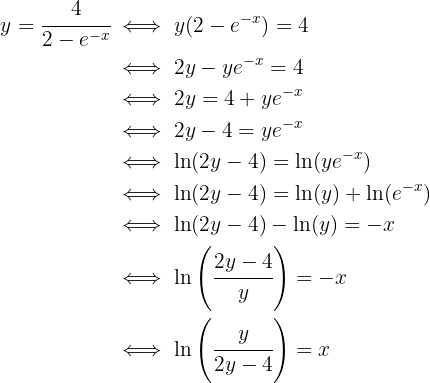
Das heißt:
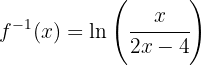
Mit KI zusammenfassen:












