In diesem Artikel üben wir das Formulieren von analytischen Ausdrücken und Graphen von linearen, quadratischen, logarithmischen sowie exponentiellen Funktionen.
Berechne die Koeffizienten der Funktion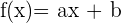 
, wenn 
und 
.
- Stelle die Funktion dar
- Gib die Intervalle an, in denen die Abbildung der Funktion positiv und negativ ist.
Berechne die Koeffizienten der Funktion 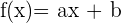, wenn und .
A Die Darstellung der Funktion ist ihr analytischer und grafischer Ausdruck.
Um den Wert von b zu bestimmen, nutzen wir, dass :
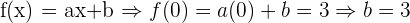
Um nun den Wert von a zu ermitteln, nutzen wir, dass und dass 
:
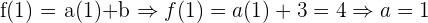
Somit lautet der analytische Ausdruck: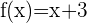 
.
Für die grafische Darstellung können wir aus dem analytischen Ausdruck ableiten, dass die Funktion linear ist (weil die Potenz von x gleich 1 ist), also eine Gerade ist, und um sie zu konstruieren, reichen zwei Punkte aus. eIn diesem Fall können wir die Nullstellen auf den Achsen berücksichtigen, oder wir können die Punkte nehmen, wenn und und die Gerade zeichnen, die beide enthält, wie in der folgenden Grafik gezeigt:
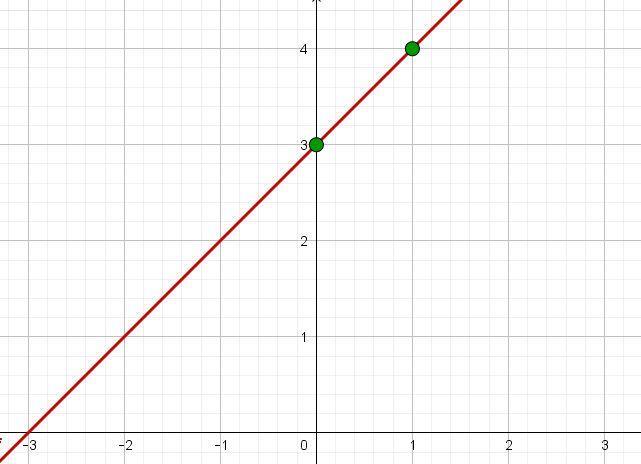
B Gib die Intervalle an, in denen die Abbildung der Funktion positiv oder negativ ist.
Aus der obigen Grafik lässt sich ableiten, dass die Abbildungen der Funktion negativ sind, wenn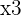 
.
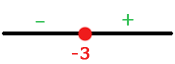
Zur analytischen Lösung setzen wir 0 und lösen die Gleichung:
Wir geben zwei Werte an, einen kleiner als -3 und einen größer als -3:
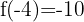
Links von -3 haben wir ein negatives Intervall und rechts davon ein positives Intervall
Stelle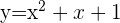 
grafisch dar
Um den Graphen der Parabel zu erstellen, benötigen wir den Scheitelpunkt und die Schnittpunkte mit den Koordinatenachsen.
.
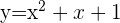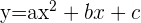ist 
.Somit haben wir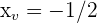 
, weshalb 
.
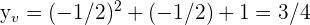Der Scheitelpunkt lautet: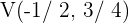 
.
2 Schnittpunkt von 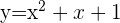mit der x-Achse
Wir müssen herausfinden, ob es für x solche Werte gibt, dass 
so ist, dass 
. Da die Determinante der Gleichung gleich 0 ist, gibt es keine reellen Lösungen (da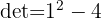 
, dann ist 
. Der Schnittpunkt ist also 
.
Abschließend stellen wir anhand der oben genannten Informationen grafisch dar:
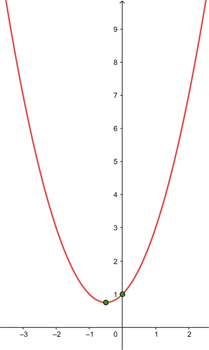
Eine Parabel hat ihren Scheitelpunkt im Punkt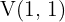 
und geht durch den Punkt 
. Finde ihre Gleichung.
Eine Parabel hat ihren Scheitelpunkt im Punkt 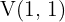und geht durch den Punkt . Finde ihre Gleichung.
Eine Funktion der Form 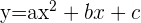, hat den Scheitelpunkt 
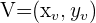. Um die Koordinate 
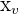zu berechnen, wird Folgendes verwendet:
.
Da die Koordinate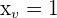 
ist, setzen wir ein und erhalten Folgendes:
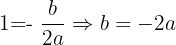
Wir setzen die uns bekannten Punkte in die Funktio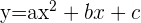n ein:
.
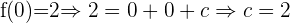
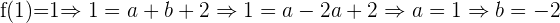Schließlich können wir die Funktion schreiben, indem wir die erhaltenen Werte in 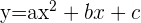einsetzen: 
.
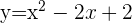Finde den analytischen Ausdruck der Funktion
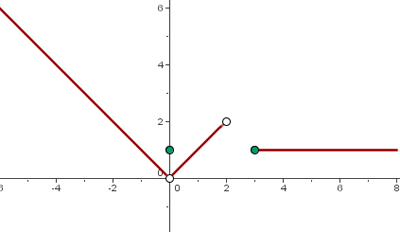
Finde den analytischen Ausdruck der Funktion
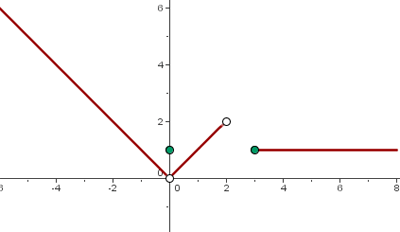
Wie wir sehen, ist die Funktion abschnittsweise definiert. Mithilfe der Punkt-Steigungs-Form können wir die Gleichung jeder der Funktionen ermitteln, um schließlich den folgenden Ausdruck zu erhalten:
Stelle die folgenden Funktionen grafisch dar:
A Stelle die Funktion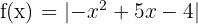 
dar
Zunächst setzen wir die Funktion gleich 0, ohne den Betrag, und berechnen ihre Nullstellen:
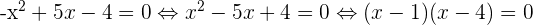
Somit ist 
oder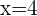 
.
Anschließend bilden wir mit den Nullstellen Intervalle und werten das Vorzeichen der einzelnen Intervalle aus
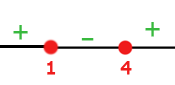
Wir definieren die Funktion abschnittsweise, wobei wir berücksichtigen, dass auf den Intervallen, auf denen x negativ ist, sich das Vorzeichen der Funktion ändert:
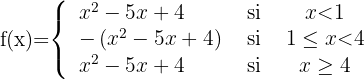
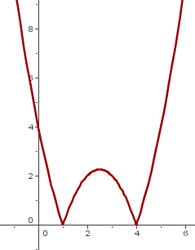
Schließlich stellen wir die Funktion grafisch dar:
B Stelle die Funktion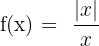 
dar
Schließlich stellen wir grafisch dar:
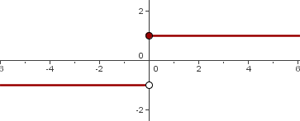
Stelle die Funktion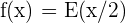 
dar
Stelle die Funktion 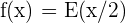dar
Um die Aufgabe zu lösen, werden zunächst einige Werte tabellarisch und dann grafisch dargestellt:
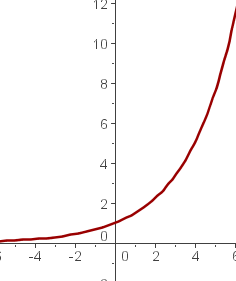
Stelle die Exponentialfunktion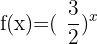 
dar
Zur Lösung werden zunächst einige Werte tabellarisch und dann grafisch dargestellt:
Stelle die Logarithmusfunktion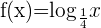 
dar
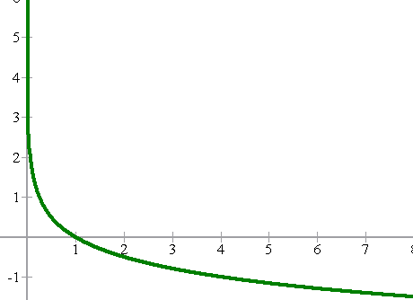
Stelle die Logarithmusfunktion 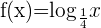dar.
Zur Lösung werden zunächst einige Werte tabellarisch und dann grafisch dargestellt:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
