y = 2
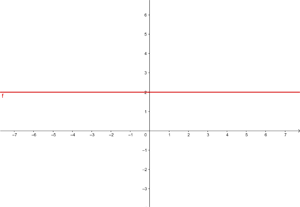
Stelle die konstante Funktion dar:
y = 2
Diese Funktion bezieht sich auf alle Punkte der Koordinaten (x,y), wobei y=2. Das heißt, auf alle Punkte (x,2), wobei x eine unabhängige Variable ist, der ein beliebiger Wert zugewiesen werden kann. Zum Beispiel (1,2) (-4,2) (5,2) etc.
y = –2
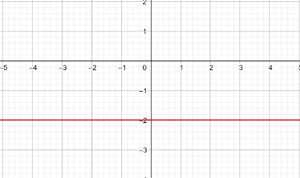
Stelle die konstante Funktion dar:
y = −2
Diese Funktion bezieht sich auf alle Punkte der Koordinaten (x,y), wobei y=-2. Das heißt, auf alle Punkte (x, -2), wobei x eine unabhängige Variable ist, der ein beliebiger Wert zugewiesen werden kann. Zum Beispiel (1,-2) (-4,-2) (5,-2) etc.
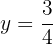
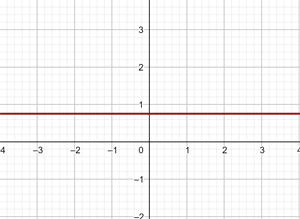
Stelle die konstante Funktion dar:
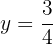
Diese Funktion bezieht sich auf die Punkte der Koordinaten (x,y) , wobei 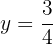. Das heißt, auf alle Punkte 
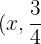), wobei x eine unabhängige Variable ist, der ein beliebiger Wert zugewiesen werden kann. Zum Beispiel:
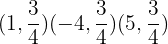
y = 0
Stelle die konstante Funktion dar:
y = 0
Diese Funktion bezieht sich auf die Punkte der Koordinaten (x,y), wobei y=0. Das heißt, auf alle Punkte (x,0), wobei x eine unabhängige Variable ist, der ein beliebiger Wert zugewiesen werden kann. Zum Beispiel (1,0) (-4,0) (5,0) etc.
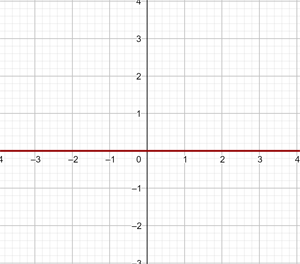
x = 0
Stelle die vertikale Gerade dar:
x = 0
Hierbei handelt es sich nicht um eine Funktion. Die Gerade bezieht sich auf alle Punkte der Koordinaten (x,y), wobei x=0. Das heißt, auf alle Punkte (0,y), wobei y eine unabhängige Variable ist, der ein beliebiger Wert zugewiesen werden kann. Zum Beispiel (0,1) (0,-3) (0,5) etc.
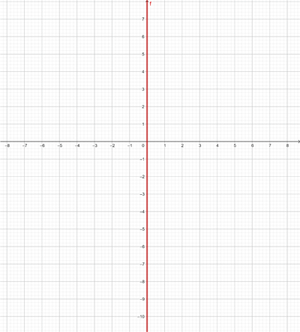
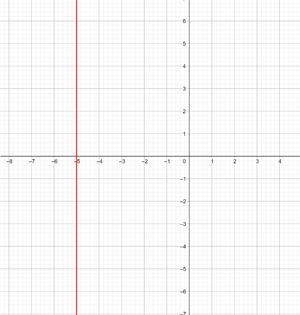
x = −5
Stelle die vertikale Gerade dar
x = −5
Diese Funktion bezieht sich auf alle Punkte der Koordinaten (x,y), wobei x=-5. Das heißt, auf alle Punkte (-5,y), wobei y eine unabhängige Variable ist, der ein beliebiger Wert zugewiesen werden kann. Zum Beispiel (-5,1) (-5,-3) (-5,5) etc.
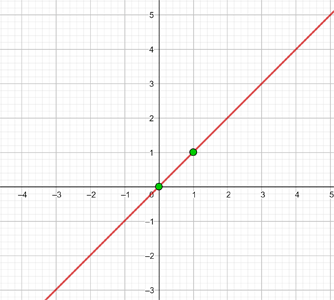
y = x
Stelle folgende Funktion dar:
y=x
Diese Funktion bezieht sich auf alle Punkte der Koordinaten (x,y), wobei y=x. Das heißt, auf alle Punkte (x,y), wobei y=x eine unabhängige Variable ist, der ein beliebiger Wert zugewiesen werden kann. Zum Beispiel (1,1) (-3,-3) (5,5) etc.
Um eine effiziente Darstellung zu ermöglichen, erstellen wir eine Tabelle, in die wir auf der linken Seite die Werte von x (jeden beliebigen Wert) und auf der rechten Seite den Wert, den y nach der Auswertung des x in unserer Funktion zugewiesenen Wertes annimmt, eintragen.
y = 2x
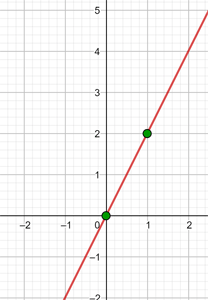
Stelle die lineare Funktion dar:
y = 2x
Um eine effiziente Darstellung zu ermöglichen, erstellen wir eine Tabelle, in die wir auf der linken Seite die Werte von x (jeden beliebigen Wert) und auf der rechten Seite den Wert, den y nach der Auswertung des x in unserer Funktion zugewiesenen Wertes annimmt, eintragen.
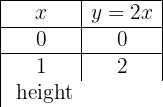
y = 2x − 1
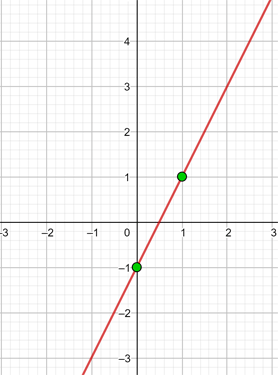
Stelle die Funktion dar:
y = 2x − 1
Um eine effiziente Darstellung zu ermöglichen, erstellen wir eine Tabelle, in die wir auf der linken Seite die Werte von x (jeden beliebigen Wert) und auf der rechten Seite den Wert, den y nach der Auswertung des x in unserer Funktion zugewiesenen Wertes annimmt, eintragen.
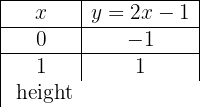
y = −2x − 1
Stelle die Funktion dar:
y = −2x − 1
Um eine effiziente Darstellung zu ermöglichen, erstellen wir eine Tabelle, in die wir auf der linken Seite die Werte von x (jeden beliebigen Wert) und auf der rechten Seite den Wert, den y nach der Auswertung des x in unserer Funktion zugewiesenen Wertes annimmt, eintragen.
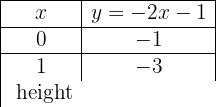
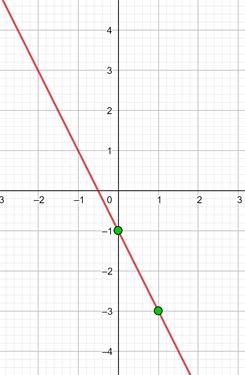
Stelle die Funktion dar: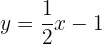
Stelle die Funktion dar:
Um eine effiziente Darstellung zu ermöglichen, erstellen wir eine Tabelle, in die wir auf der linken Seite die Werte von x (jeden beliebigen Wert) und auf der rechten Seite den Wert, den y nach der Auswertung des x in unserer Funktion zugewiesenen Wertes annimmt, eintragen.
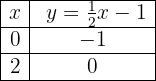
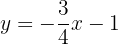
Stelle die Funktion dar:
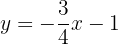
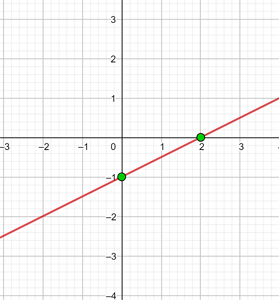
Um eine effiziente Darstellung zu ermöglichen, erstellen wir eine Tabelle, in die wir auf der linken Seite die Werte von x (jeden beliebigen Wert) und auf der rechten Seite den Wert, den y nach der Auswertung des x in unserer Funktion zugewiesenen Wertes annimmt, eintragen.
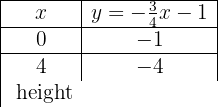
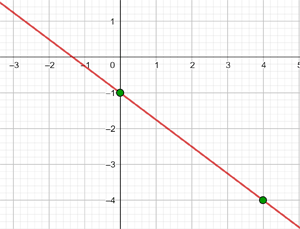
Die Funktion hat die Steigung −3 und schneidet die y-Achse bei −1.
Stelle folgende Funktion dar. Dabei ist bekannt:
Die Funktion hat die Steigung −3 und schneidet die y-Achse bei −1.
y = -3x -1
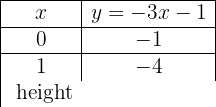
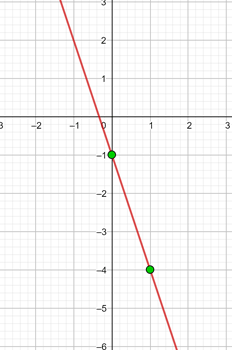
Die Funktion hat die Steigung 4 und verläuft durch den Punkt (−3, 2).
Die Funktion hat die Steigung 4 und verläuft durch den Punkt (−3, 2).
Die Funktion hat die Form: y = mx + n
m = 4, wir setzen den Wert für m ein: y = 4x + n
Ein Punkt ist (−3, 2), wir setzen die Werte ein: 2 = 4 · (−3) + n n = 14
y = 4 x + 14
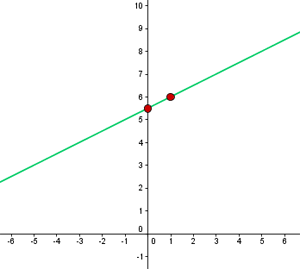
Verläuft durch die Punkte A(−1, 5) und B(3, 7).
Verläuft durch die Punkte A(−1, 5) und B(3, 7).
Die Funktion hat die Form: y = mx + n
Verläuft durch (−1, 5): 5 = −m + n
Verläuft durch (3, 7) : 7 = 3m + n
Wir lösen das Gleichungssystem wie folgt:
−5 = m − n
7 = 3m + n
2 = 4m 
m = ½ n = 11/2
Die Funktion ist: 
Verläuft durch den Punkt P(2, −3) und ist parallel zur der Geraden mit der Gleichung y = −x + 7.
Verläuft durch den Punkt P(2, −3) und ist parallel zur der Geraden mit der Gleichung y = −x + 7.
Die Funktion ist : y = mx + n
Zwei parallele Geraden haben die gleiche Steigung, m = –1
Verläuft durch (2, −3):−3 = −1 · 2 + n n = − 1
Die Funktion ist : y = −x − 1
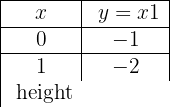
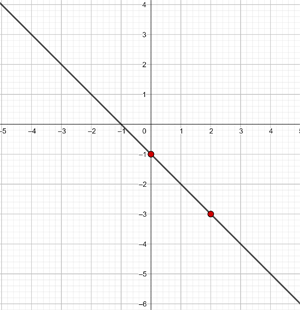
In den ersten 10 Wochen des Anbaus einer Pflanze, die eine Größe von 2 cm hatte, wurde festgestellt, dass ihr Wachstum direkt proportional zur Zeit ist, wobei die Pflanze in der ersten Woche 2,5 cm groß war. Stelle eine affine Funktion auf, die die Höhe der Pflanze als Funktion der Zeit angibt, und stelle sie grafisch dar.
Anfängliche Größe = 2 cm
Wöchentliches Wachstum = 2,5 − 2 = 0,5
y = 0,5 x + 2
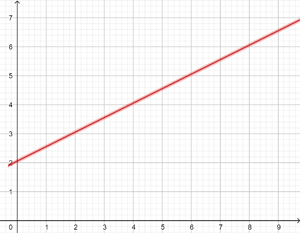
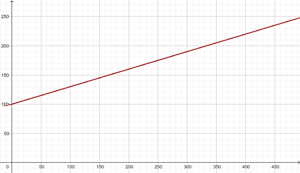
Für einen Mietwagen werden täglich 100 € plus 0,30 € pro gefahrenem Kilometer berechnet.
Stelle die Gleichung der Geraden auf, die die täglichen Kosten mit der Anzahl der Kilometer verbindet und stelle sie grafisch dar.
Wenn an einem Tag insgesamt 300 km gefahren werden, wie viel muss dann bezahlt werden?
y = 0,3 x + 100
y = 0,3 · 300 + 100 = 190 €
Berechne die Koeffizienten der Funktion: (x) = ax + b, wenn f(0) = 3 und f(1) = 4.
f(0) = 3
3 = a · 0 + b b = 3
f(1) = 4
4 = a · 1 + b a = 1
f(x) = x + 3
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
