Kapitel
Bevor wir mit den Aufgaben beginnen, sehen wir uns die Grundlagen an.
Was ist eine quadratische Funktion?
Eine quadratische Funktion ist eine Polynomfunktion vom Grad 2 der Form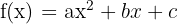 
, wobei 
relle Zahlen sind und 
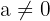
Der Graph einer quadratischen Funktion ist immer ein Kegelschnitt (Kreis, Ellipse, Parabel oder Hyperbel), allerdings beschäftigen wir uns in diesem Artikel nur mit quadratischen Funktionen von Parabeln.
Der Graph von 
(die einfachste quadratische Funktion) zeigt einige Eigenschaften von Parabeln auf. Unter anderem ist 
und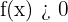 
für jeden anderen reellen Wert von 
. Daher hat die Funktion ein Minimum im Punkt 
, der als Scheitelpunkt der Parabel bezeichnet wird.
Wenn 
, ist die Parabel nach oben geöffnet
Wenn 
, ist die Parabel nach unten geöffnet
Wie wird eine quadratische Funktion gelöst und wie kann sie dargestellt werden?
Es gibt zwei Methoden, um eine quadratische Funktion zu lösen und darzustellen. Im Folgenden sind die jeweiligen Schritte aufgeführt:
Scheitelpunktformel
1Bestimme die Werte für .
2Bestimme den Wert für des Scheitelpunkts mit der entsprechenden Formel.
3Bestimme den Wert für 
, indem du den Wert für einsetzt
4Ermittle die Koordinaten 
.
Das Quadrat auflösen
1Schreibe die Gleichung.
2Dividiere durch den Wert des Terms 
.
3Bringe das konstante Glied der Gleichung auf die rechte Seite.
4Vervollständige das Quadrat auf der linken Seite der Gleichung.
5Faktorisiere die linke Seite der Gleichung.
6Ermittle und schreibe die Koordinaten .
Beispielaufgaben
Ermittle den Scheitelpunkt und die Gleichung der Symmetrieachse der folgenden Parabeln
1 
;
2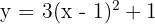 
;
3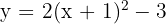 
;
4 
;
5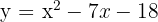 
;
6 
;
Der Scheitelpunkt der Parabel 
ist gegeben durch 
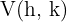und die Symmetrieachse durch 
. Für die Parabel 
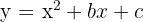ist der Scheitelpunkt gegeben durch: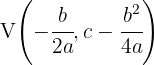 
1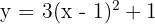
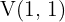
2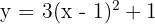
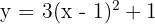
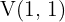
3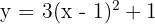
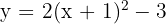
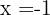
4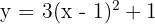
5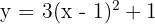
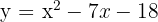
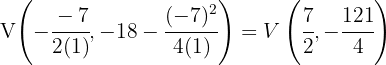
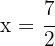
6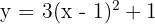
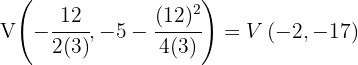
Gib an, ohne sie zu zeichnen, in wie vielen Punkten die folgenden Parabeln die x-Achse schneiden
1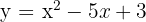 
;
2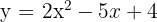 
;
3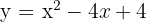 
;
4 
.
Wir wenden die Determinante
und schließen aus ihrem Vorzeichen, ob die Parabeln die x-Achse zweimal, einmal oder überhaupt nicht schneiden.
1 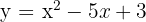Wir berechnen die Determinante
Da die Determinante positiv ist, gibt es zwei Schnittpunkte.
2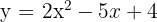
Wir berechnen die Determinante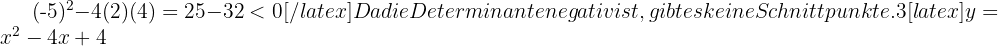
Wir berechnen die Determinante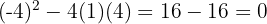
Da die Determinante null ist, gibt es einen Schnittpunkt.
4
Wir berechnen die Determinante
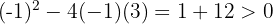
Da die Determinante positiv ist, gibt es zwei Schnittpunkte.
Ermittle die gesuchten Elemente in jeder der folgenden Funktionen
Eine quadratische Funktion hat die Form
und verläuft durch den Punkt
.
Berechne den Wert für 
.
1 Wir setzen den Punkt in die Funktion ein
2 Wir lösen nach 
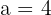auf
Bekannt ist, dass die Funktion der Form
durch die Punkte 
und 
verläuft.
Berechne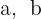 
und 
.
1 Wir setzen den Wert jedes Punkts ein:
2 Wir erhalten folgendes Gleichungssystem
3 Wir lösen das System und erhalten 
Der Scheitelpunkt einer Parabel ist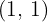 
und sie verläuft durch den Punkt 
. Bestimme ihre Gleichung.
1 Die Gleichung hat die Form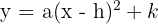
2 Wir setzen die Werte des Scheitelpunkts ein:
3 Wir setzen die Werte des Punkts , durch den die Parabel verläuft, ein und ermitteln 
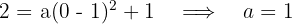
4 Wir setzen den Wert für ein und berechnen
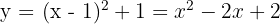
Stelle ausgehend vom Graphen der Funktion dar:
1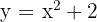 
;
2 
;
3 
;
4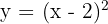 
;
5 
;
6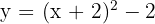 
.
Wir wenden den Graphen 
an
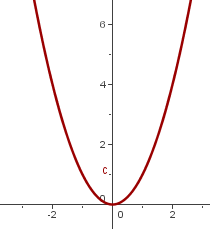
1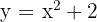
Wir verschieben den Graphen von so, dass der Scheitelpunkt sich bei befindet
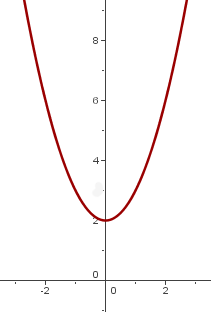
2
Wir verschieben den Graphen von so, dass der Scheitelpunkt sich bei 
befindet
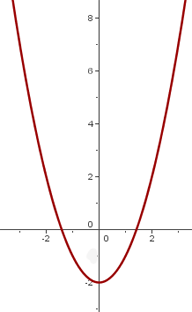
3
Wir verschieben den Scheitelpunkt von so, dass sich der Scheitelpunkt bei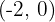 
befindet
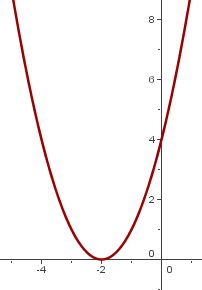
4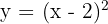
Wir verschieben den Graphen von so, dass der Scheitelpunkt sich bei 
befindet
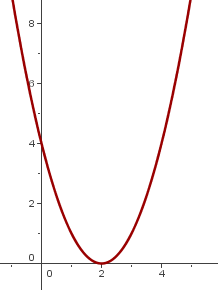
5
Wir verschieben den Graphen von so, dass der Scheitelpunkt sich bei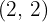 
befindet
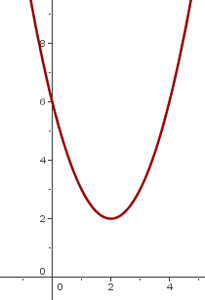
6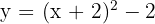
Wir verschieben den Graphen von so, dass sich der Scheitelpunkt bei 
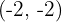befindet
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
