Kapitel
Es soll ein Grenzwert der folgenden Form berechnet werden:
Hierfür ersetzen wir 
durch 
.
Dieses Verfahren funktioniert jedoch nicht immer, da in manchen Situationen nicht klar ist, welchen Wert die Funktion annehmen wird, wenn sie für ausgewertet wird. Im Folgenden werden einige Situationen beschrieben, in denen der Wert des Grenzwerts nicht eindeutig ist und wie er bestimmt werden kann:
Grenzwert von Polynomfunktionen im Bereich von unendlich
Wir sehen uns ein Polynom der folgenden Form an
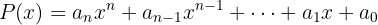
Somit lautet der Grenzwert
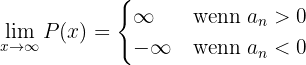
Mit anderen Worten: Das Vorzeichen des Grenzwerts ist das gleiche wie das Vorzeichen des Leitkoeffizienten des Polynoms.
Beispiele
1. Der folgende Grenzwert
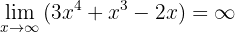
ist , da der Leitkoeffizient (also 3) positiv ist.
2. Der Grenzwert
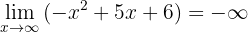
nimmt den Wert 
an, da der Leitkoeffizient negativ ist 
.
Hinweis: Im obigen Beispiel ist zu beachten, dass das Ersetzen von durch bei der Berechnung des Grenzwertes nicht hilfreich ist, da
Das heißt, wir haben eine Unbestimmtheit der Form 
.
Grenzwert der Umkehrfunktion eines Polynoms im Bereich von unendlich
Wenn 
ein Polynom der Ordnung größer oder gleich 1 ist, ist der Grenzwert von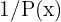 
, wenn 
, gegeben durch
Sehen wir uns zum Beispiel folgenden Grenzwert an:
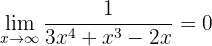
Berechnung des Grenzwerts, wenn x gegen minus unendlich konvergiert
Um die Grenzwerte zu berechnen, wenn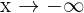 
, halten wir uns ganz einfach an folgende Eigenschaft:
Somit ist der Grenzwert, wenn 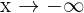, gleichbedeutend mit der Berechnung eines Grenzwerts, wenn .
Beispiele
1. Wir nehmen den Grenzwert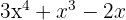 
, wenn . Somit
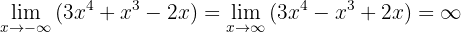
2. Wir sehen uns den folgenden Grenzwert an
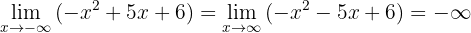
3. Nun sehen wir uns den Grenzwert mit einer Wurzel an
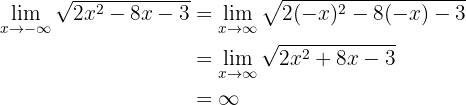
Wir beachten, dass
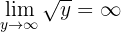
4. Zuletzt sehen wir uns einen weiteren Grenzwert mit einer Wurzel an:
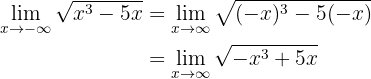
In diesem Fall existiert der Grenzwert nicht, da der Radikand negative Werte annimmt.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
