Zeige, dass die Funktion  die x-Achse auf dem Intervall
die x-Achse auf dem Intervall  schneidet. Gilt dies auch für die Funktion
schneidet. Gilt dies auch für die Funktion  ?
?
Zeige, dass die Funktion  die x-Achse auf dem Intervall
die x-Achse auf dem Intervall  schneidet. Gilt dies auch für die Funktion
schneidet. Gilt dies auch für die Funktion  ?
?
1 Die Funktion ist stetig im gesamten Bereich  .
.
2  .
.
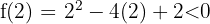
3 Da der Satz von Bolzano erfüllt ist, existiert mindestens ein  , das zum Intervall
, das zum Intervall  gehört und die x-Achse schneidet.
gehört und die x-Achse schneidet.
4 Das Gleiche gilt für die 2. Funktion, da sie nicht stetig bei  ist.
ist.
Gegeben ist die Funktion:

Kann bestätigt werden, dass  auf dem Intervall
auf dem Intervall  beschränkt ist?
beschränkt ist?
Gegeben ist die Funktion:

Kann bestätigt werden, dass  auf dem Intervall
auf dem Intervall  beschränkt ist?
beschränkt ist?
1 Die Funktion  ist nicht stetig bei
ist nicht stetig bei  .
.
2 Somit ist die Funktion auf dem geschlossenen Intervall  nicht stetig.
nicht stetig.
3 Folglich können wir nicht behaupten, dass die Funktion auf diesem Intervall beschränkt ist.
Gegeben ist die Funktion  . Kann bestätigt werden, dass die Funktion alle Werte des Intervalls
. Kann bestätigt werden, dass die Funktion alle Werte des Intervalls  annimmt?
annimmt?
Gegeben ist die Funktion  . Kann bestätigt werden, dass die Funktion alle Werte des Intervalls
. Kann bestätigt werden, dass die Funktion alle Werte des Intervalls  annimmt?
annimmt?
1 Die Funktion ist im gesamten Definitionsbereich  stetig, da es sich um eine Polynomfunktion handelt.
stetig, da es sich um eine Polynomfunktion handelt.
2 Auf dem Intervall  gilt
gilt  und
und 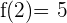 .
.
3 Aus dem Zwischenwertsatz für Ableitungen ergibt sich, dass die Funktion alle Werte auf dem Intervall  annimmt.
annimmt.
Zeige unter Verwendung des Satzes von Bolzano, dass die Gleichung:  mindestens eine Lösung
mindestens eine Lösung  hat, so dass
hat, so dass 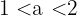 .
.
Zeige unter Verwendung des Satzes von Bolzano, dass die Gleichung:  mindestens eine Lösung
mindestens eine Lösung  hat, so dass
hat, so dass 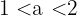 .
.
1  ist stetig bei
ist stetig bei 
2 Das Vorzeichen der Funktion ändert sich bei 
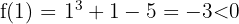
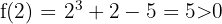
3 Da die drei vorherigen Eigenschaften erfüllt sind, existiert  , so dass:
, so dass:
 .
.
4 Es gibt also mindestens eine reelle Lösung der Gleichung 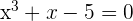 .
.
Gegeben ist die Funktion  . Kann bestätigt werden, dass mindestens ein Punkt
. Kann bestätigt werden, dass mindestens ein Punkt  innerhalb des Intervalls
innerhalb des Intervalls  exisitiert, so dass
exisitiert, so dass  ?
?
Gegeben ist die Funktion  . Kann bestätigt werden, dass mindestens ein Punkt
. Kann bestätigt werden, dass mindestens ein Punkt  innerhalb des Intervalls
innerhalb des Intervalls  exisitiert, so dass
exisitiert, so dass  ?
?
1  ist stetig bei
ist stetig bei  .
.
2 Das Vorzeichen der Funktion ändert sich bei  nicht
nicht
 .
.
 .
.
3 Der Satz von Bolzano kann nicht angewendet werden, da sich das Vorzeichen nicht ändert.
Begründe, dass die Polynomfunktion  eine Nullstelle zwischen
eine Nullstelle zwischen  y
y  hat.
hat.
Begründe, dass die Polynomfunktion  eine Nullstelle zwischen
eine Nullstelle zwischen  y
y  hat.
hat.
1 Da es sich um eine Polynomfunktion handelt, ist sie stetig auf dem Intervall  .
.
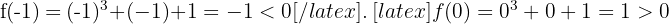 .
.
2 Da die drei vorhergehenden Eigenschaften nach dem Satz von Bolzano erfüllt sind, existiert  , so dass:
, so dass:

Zeige, dass die Gleichung  mindestens eine reelle Lösung hat.
mindestens eine reelle Lösung hat.
Zeige, dass die Gleichung  mindestens eine reelle Lösung hat.
mindestens eine reelle Lösung hat.
1 Die Funktion ist stetig auf dem Intervall  .
.
 .
.
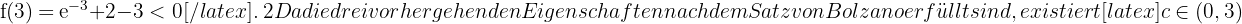 , so dass:
, so dass:
 .
.
3 Somit existiert mindestens eine reelle Lösung der Gleichung  .
.
Zeige, dass eine reelle Zahl  existiert, so dass
existiert, so dass 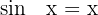 .
.
Zeige, dass eine reelle Zahl  existiert, so dass
existiert, so dass 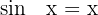 .
.
1 Wir betrachten die Funktion 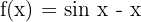 .
.
Sie ist stetig im gesamten Bereich  .
.
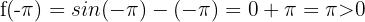
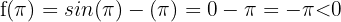
2 Da die drei vorhergehenden Eigenschaften nach dem Satz von Bolzano erfüllt sind, existiert 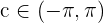 , so dass:
, so dass:

3 Somit existiert mindestens eine reelle Lösung der Gleichung 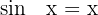 .
.
Gegeben ist die Funktion:
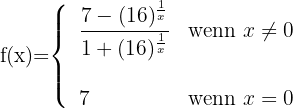
Zeige, dass es einen Punkt auf dem offenen Intervall  gibt, auf dem
gibt, auf dem  den Wert
den Wert  annimmt.
annimmt.
Gegeben ist die Funktion:
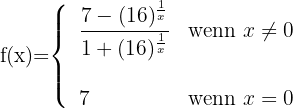
Zeige, dass es einen Punkt auf dem offenen Intervall  gibt, auf dem
gibt, auf dem  den Wert
den Wert  annimmt.
annimmt.
1 Die Exponentialfunktion ist positiv für gesamt  , da der Nenner der Funktion nicht 0 werden kann.
, da der Nenner der Funktion nicht 0 werden kann.
2 Ein Zweifel an der Stetigkeit besteht nur bei  , das sich außerhalb des zu untersuchenden Intervalls befindet. Somit ist
, das sich außerhalb des zu untersuchenden Intervalls befindet. Somit ist  stetig bei
stetig bei  .
.
3 Wir nehmen die Funktion  , die durch
, die durch  definiert ist.
definiert ist.
 ist stetig auf dem Intervall
ist stetig auf dem Intervall  .
.
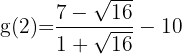
4 Da die drei vorhergehenden Eigenschaften nach dem Satz von Bolzano erfüllt sind, existiert  , so dass:
, so dass:
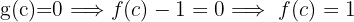
Mit KI zusammenfassen:


