Kapitel
- Definitionsmenge der Polynomfunktion
- Definitionsmenge der rationalen Funktion
- Definitionsmenge der Wurzelfunktion mit ungeradem Wurzelexponenten
- Definitionsmenge der Wurzelfunktion mit geradem Wurzelexponenten
- Definitionsbereich der Logarithmusfunktion
- Definitionsmenge der Exponentialfunktion
- Definitionsmenge der Sinusfunktion
- Definitionsmenge der Kosinusfunktion
- Definitionsmenge der Tangensfunktion
- Definitionsmenge der Kotangensfunktion
- Definitionsmenge der Sekansfunktion
- Definitionsmenge der Kosekansfunktion
- Definitionsmenge beim Rechnen mit Funktionen
- Definitionsmenge der Sinusfunktion
- Definitionsmenge der Kosinusfunktion
- Definitionsmenge der Tangensfunktion
- Definitionsmenge der Kotangensfunktion
- Definitionsmenge der Sekansfunktion
- Definitionsmenge der Kosekansfunktion
- Definitionsmenge beim Rechnen mit Funktionen
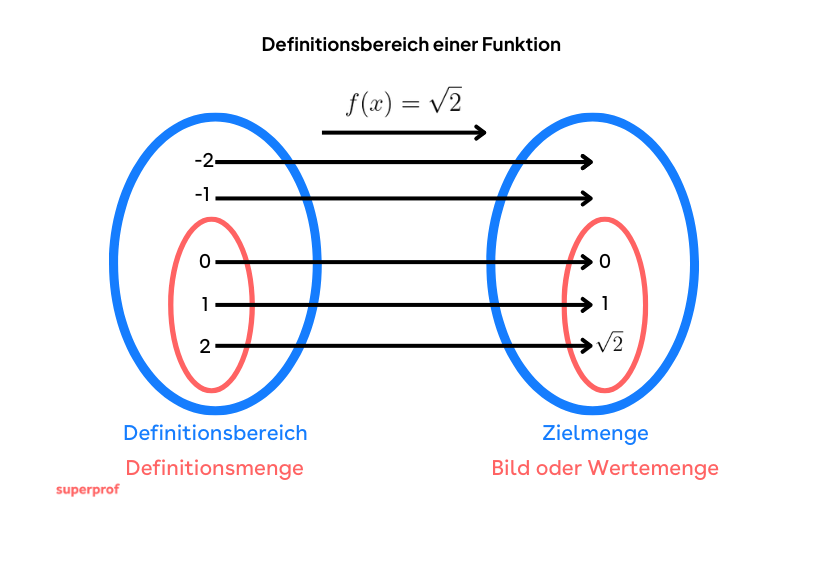
Der Definitionsbereich oder die Definitionsmenge beschreibt den Bereich, in dem eine Funktion definiert ist.
Das heißt, es handelt sich um die Werte von  , die wir in eine Funktion einsetzen können, um den entsprechenden Wert für
, die wir in eine Funktion einsetzen können, um den entsprechenden Wert für  zu erhalten.
zu erhalten.
Mathematisch ausgedrückt:

Dies bedeutet, dass der Definitionsbereich einer Funktion diejenigen Werte von  sind, die zu den reellen Zahlen gehören und für die ein entsprechender Wert der Funktion
sind, die zu den reellen Zahlen gehören und für die ein entsprechender Wert der Funktion  existiert.
existiert.
Die Teilmenge der reellen Zahlen, in der die Funktion definiert ist, nennt man Definitionsmenge oder Definitionsbereich.
Sie wird mit D bezeichnet.
Die Variable x, die zur Definitionsmenge gehört, wird unabhängige Variable genannt.

Definitionsmenge der Polynomfunktion
Der Definitionsbereich einer Polynomfunktion ist  .
.
Außerdem steht bei Polynomfunktionen eine Zahl (konstantes Glied) im Nenner:
Beispiele für die Definitionsmenge von Polynomfunktionen
1 

2 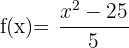

Du kannst irgendeinen Wert für  in die Funktionen einsetzen und erhältst immer den entsprechenden Wert für
in die Funktionen einsetzen und erhältst immer den entsprechenden Wert für  .
.
Definitionsmenge der rationalen Funktion
Die Definitionsmenge ist  minus die Werte, für die der Nenner null wird (es kann keinen Bruch geben, dessen Nenner null ist).
minus die Werte, für die der Nenner null wird (es kann keinen Bruch geben, dessen Nenner null ist).
Beispielaufgabe
1 Wie lautet die Definitionsmenge der Funktion 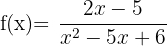 ?
?
Wir setzen den Nenner  und lösen die Gleichung
und lösen die Gleichung

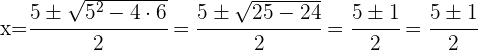



Definitionsmenge der Wurzelfunktion mit ungeradem Wurzelexponenten
Die Definitionsmenge ist die Definitionsmenge des Radikanden der Funktion.
1

2

Definitionsmenge der Wurzelfunktion mit geradem Wurzelexponenten
Die Definitionsmenge besteht aus allen Werten, die den Radikanden größer oder gleich null machen.
1



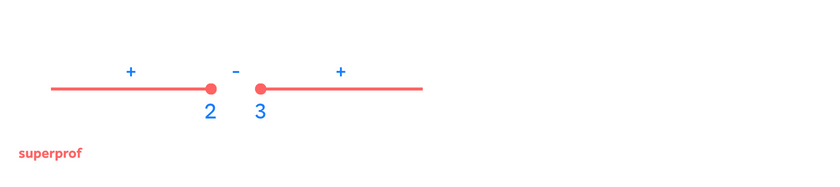
2



3Wie lautet die Definitionsmenge der Funktion  ?
?
In diesem Fall muss der Nenner größer als null sein und wir müssen die Werte für  finden, sodass die Wurzel existiert. Somit:
finden, sodass die Wurzel existiert. Somit:

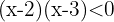


4Bestimme die Definitionsmenge der Funktion  .
.
Der Radikand muss größer als null und der Nenner muss ungleich null sein


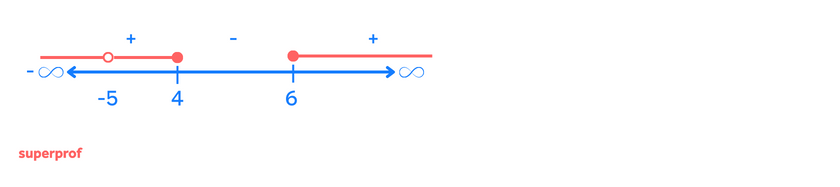
5 Bestimme die Definitionsmenge der Funktion  .
.
Da der Radikand größer oder gleich null sein muss, stellen wir folgende Ungleichung auf:

Wir lösen die quadratische Gleichung


Die Nullstellen lauten:  und
und 
Die Intervalle sind also:
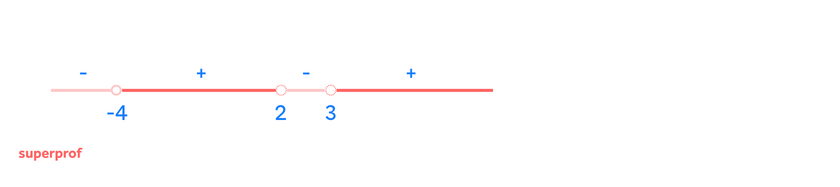
Die Definitionsmenge sind die Werte kleiner als einschließlich -2 und größer als einschließlich 7.

6 Bestimme die Definitionsmenge der Funktion 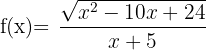 .
.
In diesem Fall müssen zwei Bedingungen gelten. Eine für den Quotienten, eine für die Wurzel. Der Zähler muss größer oder gleich null sein und der Nenner muss ungleich null sein. Somit:



Definitionsbereich der Logarithmusfunktion
Der Definitionsbereich besteht aus allen Werten, die die Funktion innerhalb des Logarithmus größer als null machen.

Es muss gelten:


Definitionsmenge der Exponentialfunktion
Beispiele
1 

2 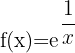
Die Definitionsmenge ist gleich  minus die Werte, für die der Nenner des Exponenten null wird.
minus die Werte, für die der Nenner des Exponenten null wird.

latex]D=(-\infty ,2]\cup [3,\infty )[/latex]

3 
Die Definitionsmenge ist der Definitionsbereich der Wurzel

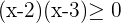
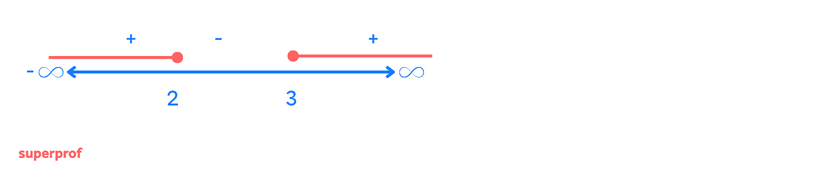


Definitionsmenge der Sinusfunktion
Die Definitionsmenge der Sinusfunktion ist 
Definitionsmenge der Kosinusfunktion
Die Definitionsmenge der Kosinusfunktion ist 
Definitionsmenge der Tangensfunktion


Definitionsmenge der Kotangensfunktion


Definitionsmenge der Sekansfunktion


Definitionsmenge der Kosekansfunktion


Definitionsmenge beim Rechnen mit Funktionen

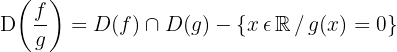




3 
Die Definitionsmenge ist der Definitionsbereich der Wurzel

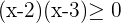



Definitionsmenge der Sinusfunktion
Die Definitionsmenge der Sinusfunktion ist 
Definitionsmenge der Kosinusfunktion
Die Definitionsmenge der Kosinusfunktion ist 
Definitionsmenge der Tangensfunktion


Definitionsmenge der Kotangensfunktion


Definitionsmenge der Sekansfunktion


Definitionsmenge der Kosekansfunktion


Definitionsmenge beim Rechnen mit Funktionen

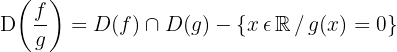




Mit KI zusammenfassen:













