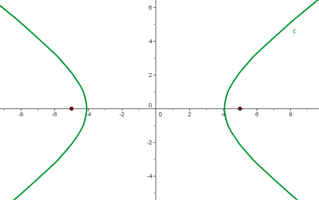
Die Hyperbel ist der geometrische Ort der Punkte der Ebene, deren Differenz des Abstands zu den Fixpunkten, genannt Brennpunkte, absolut konstant ist.
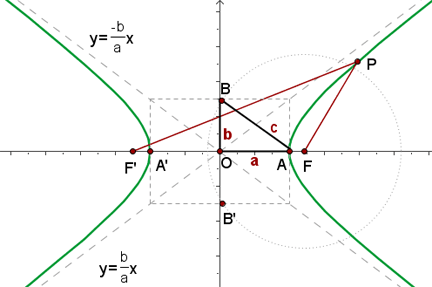
In der oben abgebildeten Grafik bedeutet dies, dass 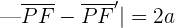 für jeden beliebigen Punkt
für jeden beliebigen Punkt  auf der Hyperbel gilt.
auf der Hyperbel gilt.

Elemente der Hyperbel
1 Brennpunkte: Dies sind die Fixpunkte  und
und 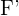 .
.
2 Brennachse oder Hauptachse: Die Gerade, die durch die Brennpunkte verläuft.
3 Nebenachse: Die Mittelsenkrechte des Segments 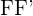 .
.
4 Mittelpunkt: Der Schnittpunkt der Achsen.
5 Scheitelpunkte: Die Punkte  und
und  sind die Punkte, an denen die Hyperbel die Brennachse schneidet.
sind die Punkte, an denen die Hyperbel die Brennachse schneidet.
6 Ortsvektoren: Die Abschnitte zwischen einem Punkt auf der Hyperbel und den Brennpunkten:  und
und  .
.
7 Brennstrecke: Der Abschnitt 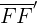 mit der Länge
mit der Länge  .
.
8 Hauptachse: Der Abschnitt  mit der Länge
mit der Länge  .
.
9 Nebenachse: Der Abschnitt  mit der Länge
mit der Länge  .
.
Die Punkte  und
und  ergeben sich aus dem Schnittpunkt der Nebenachse mit dem Kreis, dessen Mittelpunkt einer der Scheitelpunkte ist und der den Radius
ergeben sich aus dem Schnittpunkt der Nebenachse mit dem Kreis, dessen Mittelpunkt einer der Scheitelpunkte ist und der den Radius  hat.
hat.
10 Symmetrieachsen: Die Geraden, die die Haupt- oder Nebenachse enthalten.
11 Asymptoten: Die Geraden der Gleichungen: 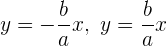
12 Verhältnis zwischen den Halbachsen: 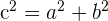
Exzentrizität der Hyperbel
Die Exzentrizität ist ein Parameter, der die Öffnung der Parabel anzeigt. Diese Zahl ist im Fall von Hyperbeln immer größer als  .
.
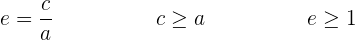
Beispiele:
- Hyperbel mit der Exzentrizität
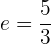
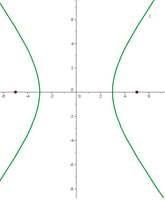
- Hyperbel mit der Exzentrizität
 . Diese Hyperbel heißt gleichseitige Hyperbel. Ihre Asymptoten sind gegeben durch
. Diese Hyperbel heißt gleichseitige Hyperbel. Ihre Asymptoten sind gegeben durch
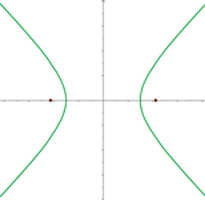
- Hyperbel mit der Exzentrizität
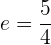
- Hyperbel mit der Exzentrizität
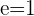
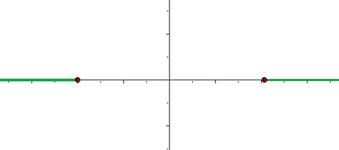
Mit KI zusammenfassen:













