Schreibe die Gleichung des Kreises mit dem Mittelpunkt 
und dem Radius  .
.
Bestimme die Gleichung des Kreises mit dem Mittelpunkt  und dem Radius
und dem Radius  .
.
Wir setzen die Werte in die allgemeine Gleichung des Kreises ein: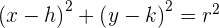
Hierbei gilt:
 sind die Koordinaten des Mittelpunktes und
sind die Koordinaten des Mittelpunktes und  ist der Radius.
ist der Radius.
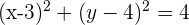
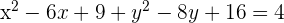
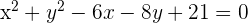
Bestimme den Mittelpunkt und den Radius eines Kreises mit der Gleichung  .
.
Bestimme den Mittelpunkt und den Radius eines Kreises mit der Gleichung  . Wir bringen die Gleichung in die gewöhnliche Form
. Wir bringen die Gleichung in die gewöhnliche Form 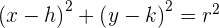 . Dazu gehen wir wie folgt vor:
. Dazu gehen wir wie folgt vor:
1 Wir schreiben die Gleichung um, indem wir die Variablen  und
und  ordnen und die Trinome zum vollständigen Quadrat ergänzen
ordnen und die Trinome zum vollständigen Quadrat ergänzen
2 Wir faktorisieren die Trinome

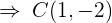 y
y 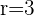
Bestimme die Koordinaten des Mittelpunkts und den Radius der Kreise:
A 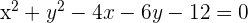
B 
C 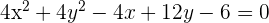
D 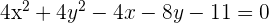
Bestimme die Koordinaten des Mittelpunkts und den Radius der Kreise:
A 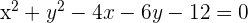 Wir bringen die Gleichung in ihre allgemeine Form:
Wir bringen die Gleichung in ihre allgemeine Form: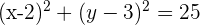
 und
und 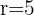
B 
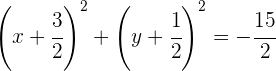 und
und 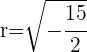
Da  imaginär ist, handelt es sich nicht um einen reellen Kreis
imaginär ist, handelt es sich nicht um einen reellen Kreis
C 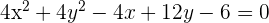
Wir dividieren durch 4 und bringen die Gleichung in ihre allgemeine Form:
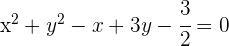
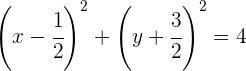
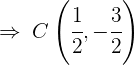 und
und 
D 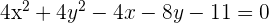
Wir dividieren durch 4 und bringen die Gleichung in ihre allgemeine Form:
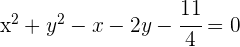
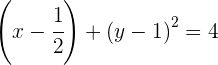
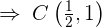 und
und 
Berechne die Gleichung eines Kreises, dessen Mittelpunkt sich bei 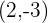 befindet und der die x-Achse tangiert.
befindet und der die x-Achse tangiert.
Berechne die Gleichung eines Kreises, dessen Mittelpunkt sich bei 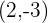 befindet und der die x-Achse tangiert.
befindet und der die x-Achse tangiert.
1 Wir stellen den Kreis mit den gegebenen Werten grafisch dar:
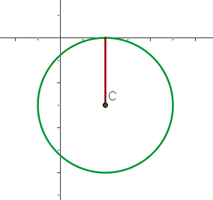
2 Aus der Abbildung können wir ableiten, dass
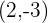

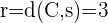
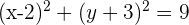
Berechne die Gleichung eines Kreises, dessen Mittelpunkt sich bei 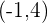 befindet und der die y-Achse tangiert.
befindet und der die y-Achse tangiert.
Berechne die Gleichung eines Kreises, dessen Mittelpunkt sich bei 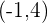 befindet und der die y-Achse tangiert.
befindet und der die y-Achse tangiert.
1 Wir stellen den Kreis mit den gegebenen Werten grafisch dar:
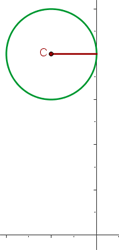
2 Aus der Abbildung können wir ableiten, dass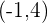
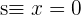
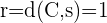

Berechne die Gleichung eines Kreises, dessen Mittelpunkt auf dem Schnittpunkt der Geraden  und
und  liegt und dessen Radius
liegt und dessen Radius  ist.
ist.
Berechne die Gleichung eines Kreises, dessen Mittelpunkt auf dem Schnittpunkt der Geraden  und
und  liegt und dessen Radius
liegt und dessen Radius  ist.
ist.
Wir stellen ein Gleichungssystem mit den gegebenen Geraden auf; die Lösung des Gleichungssystems entspricht dem Mittelpunkt des Kreises.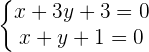

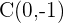
Wir setzen 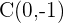 und
und 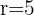 in die allgemeine Form ein
in die allgemeine Form ein
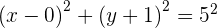
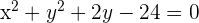
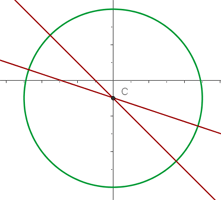
Bestimme die Gleichung des konzentrischen Kreises mit der Gleichung  , der durch den Punkt
, der durch den Punkt 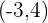 verläuft.
verläuft.
Bestimme die Gleichung des konzentrischen Kreises mit der Gleichung  , der durch den Punkt
, der durch den Punkt 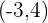 verläuft.
verläuft.
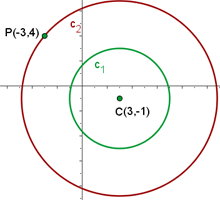
1 Da die Kreise konzentrisch sind, haben sie denselben Mittelpunkt:
2 Wir berechnen den Mittelpunkt des Kreises 
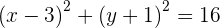
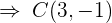
3 Um den Radius zu berechnen, berechnen wie die Entfernung von 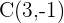 nach
nach 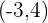

4 Wir setzen den Mittelpunkt in die allgemeine Form ein
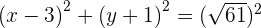

Bestimme die Gleichung des Kreises, dessen Mittelpunkt sich bei 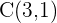 befindet und der folgende Gerade tangiert:
befindet und der folgende Gerade tangiert:  .
.
Bestimme die Gleichung des Kreises, dessen Mittelpunkt sich bei 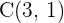 befindet und der folgende Gerade tangiert:
befindet und der folgende Gerade tangiert:  .
.
1 Der Radius wird mittels der Entfernung zwischen dem Punkt 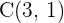 und der Geraden
und der Geraden  berechnet
berechnet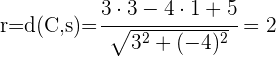
2 Wir setzen 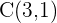 und
und  in die allgemeine Form ein
in die allgemeine Form ein
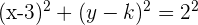
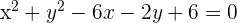
Bestimme die Gleichung des Kreises, der durch die Punkte 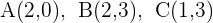 verläuft.
verläuft.
Bestimme die Gleichung des Kreises, der durch die Punkte 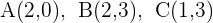 verläuft.
verläuft.
1 Betrachtet man die allgemeine Gleichung eines Kreises als  , ersetzen wir die gegebenen Punkte und bilden ein Gleichungssystem:
, ersetzen wir die gegebenen Punkte und bilden ein Gleichungssystem: 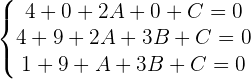
2 Wir lösen das Gleichungssystem und ersetzen es in der betrachteten Allgemeinform:
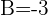
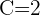

Bestimme die Gleichung des Umkreises des Dreiecks der Schnittpunkte: 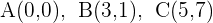 .
.
Bestimme die Gleichung des Umkreises des Dreiecks der Schnittpunkte: 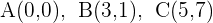 .
.
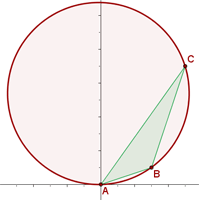
1 Wenn man bedenkt, dass die Eckpunkte des Dreiecks Punkte sind, durch die der Umkreis verläuft, kann man die Gleichung des Umfangs wie folgt formulieren  und die gegebenen Punkte ersetzen:
und die gegebenen Punkte ersetzen:
2 Wir lösen das Gleichungssystem und ersetzen es in der betrachteten Allgemeinform
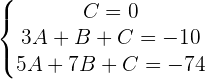
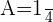

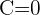
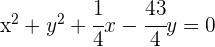
Bestimme die Gleichung eines Kreises, der durch die Punkte  und
und 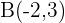 verläuft und dessen Mittelpunkt auf der folgenden Geraden liegt:
verläuft und dessen Mittelpunkt auf der folgenden Geraden liegt: 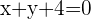 .
.
Bestimme die Gleichung eines Kreises, der durch die Punkte  und
und 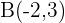 verläuft und dessen Mittelpunkt auf der folgenden Geraden liegt:
verläuft und dessen Mittelpunkt auf der folgenden Geraden liegt: 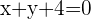 .
.
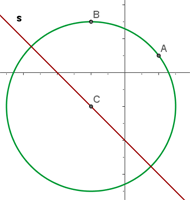
1 Wir bedenken, dass der Punkt  der Mittelpunkt des Kreises ist und sich auf der Geraden
der Mittelpunkt des Kreises ist und sich auf der Geraden 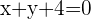 befindet. Deshalb können wir unser System bilden:
befindet. Deshalb können wir unser System bilden:
2 Aus den ersten 2 Gleichungen erhalten wir:
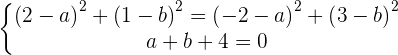
3 Wir lösen das System:
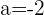

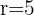
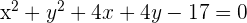
Berechne die Gleichung eines Kreises, der durch den Punkt 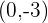 verläuft, dessen Radius
verläuft, dessen Radius  ist und dessen Mittelpunkt sich auf der Winkelhalbierenden des ersten und dritten Quadranten befindet.
ist und dessen Mittelpunkt sich auf der Winkelhalbierenden des ersten und dritten Quadranten befindet.
Berechne die Gleichung eines Kreises, der durch den Punkt 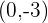 verläuft, dessen Radius
verläuft, dessen Radius  ist und dessen Mittelpunkt sich auf der Winkelhalbierenden des ersten und dritten Quadranten befindet.
ist und dessen Mittelpunkt sich auf der Winkelhalbierenden des ersten und dritten Quadranten befindet.
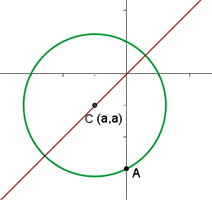
Nehmen wir an, dass der Punkt  der Mittelpunkt des Kreises ist. Außerdem ist die Winkelhalbierende des ersten und dritten Quadranten die Gerade
der Mittelpunkt des Kreises ist. Außerdem ist die Winkelhalbierende des ersten und dritten Quadranten die Gerade 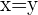 :
:


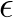

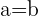

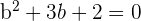
2 Wir erhalten 2 Lösungen für  :
:


3 Für 

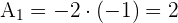
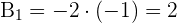
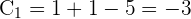
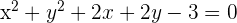
4 Für 
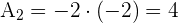
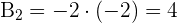
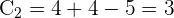
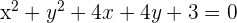
Die Extremwerte des Durchmessers eines Kreises sind die Punkte 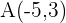 und
und  . Wie lautet die Gleichung eines solchen Kreises?
. Wie lautet die Gleichung eines solchen Kreises?
Die Extremwerte des Durchmessers eines Kreises sind die Punkte 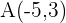 und
und 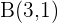
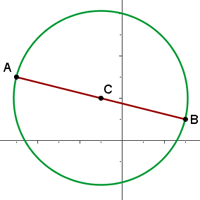
Wie lautet die Gleichung eines solchen Kreises?
1 Der Radius des Kreises ist die Mitte zwischen den Punkten  und
und  :
:
2 Der Mittelpunkt des Kreises ist der Punkt in der Mitte der Punkte  und
und  :
:

3 Wir erhalten die Koeffizienten  und
und  für die Form
für die Form

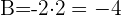
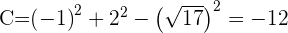

Bestimme die Gleichung eines konzentrischen Kreises zu einem Kreis  , der die Gerade
, der die Gerade 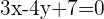 tangiert.
tangiert.
Bestimme die Gleichung eines konzentrischen Kreises zu einem Kreis  , der die Gerade
, der die Gerade 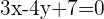 tangiert.
tangiert.
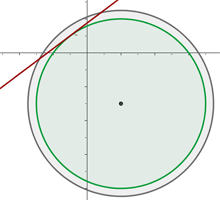
1 Wir erhalten den Mittelpunkt des Kreises mit den Koordinaten  :
:
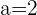
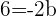
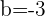
2 Der Radius ist die Entfernung zwischen  und der Geraden
und der Geraden 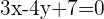 :
:
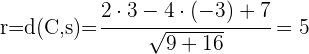
3 Wir erhalten die Koeffizienten  und
und  für die Form
für die Form 


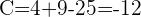
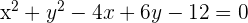
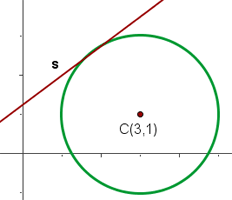
Berechne die relative Lage des Kreises 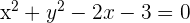 und der Geraden
und der Geraden 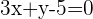 .
.
Berechne die relative Lage des Kreises 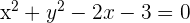 und der Geraden
und der Geraden
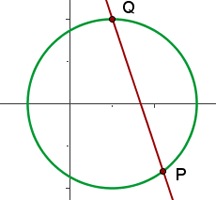
1 Wir erstellen ein Gleichungssystem aus der Gleichung des Kreises und der Gleichung der Geraden, um deren Schnittpunkte zu bestimmen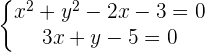
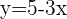
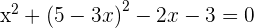
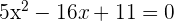

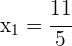
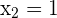
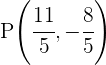

Da es zwei Schnittpunkte gibt, können wir sagen, dass die Gerade eine Sekante ist
Untersuche die relative Lage des Kreises 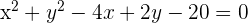 mit den Geraden:
mit den Geraden:
A 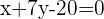
B 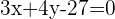
C 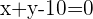
Untersuche die relative Lage des Kreises 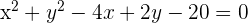 mit den Geraden:
mit den Geraden:
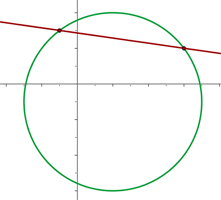
A 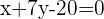
Wir erstellen ein Gleichungssystem aus der Gleichung des Kreises und der Gleichung der Geraden, um deren Schnittpunkte zu bestimmen: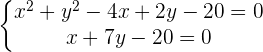

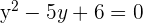
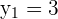

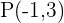

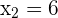
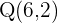
Da es zwei Schnittpunkte gibt, können wir sagen, dass die Gerade eine Sekante ist
B 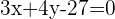
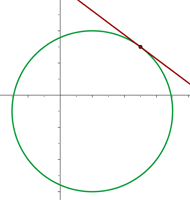
Wir erstellen ein Gleichungssystem aus der Gleichung des Kreises und der Gleichung der Geraden, um deren Schnittpunkte zu bestimmen:


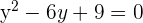



Da es nur einen Schnittpunkt zwischen dem Kreis und der Geraden gibt, ist die Gerade eine Tangente
C 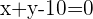
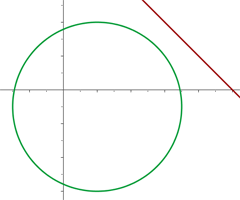
Wir erstellen ein Gleichungssystem aus der Gleichung des Kreises und der Gleichung der Geraden, um deren Schnittpunkte zu bestimmen:
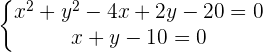
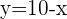

 \Delta =(-13)^{2}-4,50< 0[/latex]
\Delta =(-13)^{2}-4,50< 0[/latex]
Da es keine Schnittpunkte zwischen dem Kreis und der Geraden gibt, ist die Gerade eine Passante
Mit KI zusammenfassen:



