Definition der Umkehrfunktion
Die inverseFunktion oder Umkehrfunktion von 
ist eine weitere Funktion 
, für die gilt:
Wenn 
, ist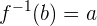 
Wir sehen uns ein Beispiel anhand der Funktion 
an
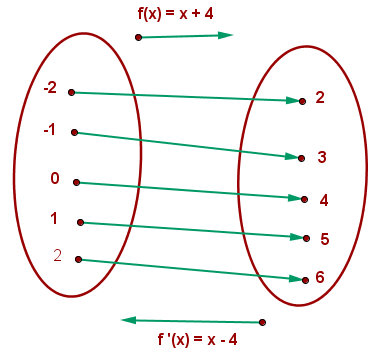
Wir stellen fest:
- Die Definitionsmenge von ist die Wertemenge von .
- Die Wertemenge von ist die Definitionsmenge von .
Wenn wir die Wertemenge einer Funktion bestimmen möchten, müssen wir die Definitionsmenge ihrer Umkehrfunktion ermitteln.
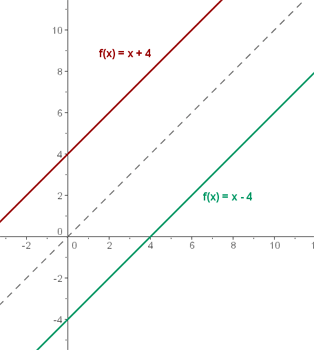
Wenn zwei Funktionen Umkehrfunktionen sind, ist ihre Komposition die identischeAbbildung.
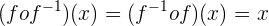
Die Graphen von und sind symmetrisch zur Winkelhalbierenden des 1. und 3. Quadranten.
Es muss zwischen der Umkehrfunktion und dem KehrwerteinerFunktion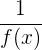 
unterschieden werden.
Der Kehrwert der Funktion ist
.
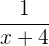Die Umkehrfunktion von ist 
, da die Komposition der beiden Funktionen die identische Abbildung ist.
Die Umkehrfunktion berechnen
Um die Umkehrfunktion einer Funktion aufzustellen oder zu berechnen, müssen folgende Schritte durchgeführt werden:
Schritt 1: Die Funktion wird mit 
und 
geschrieben .
Schritt 2: Die Variable wird in Abhängigkeit der Variablen bestimmt.
Schritt 3: Die Variablen werden vertauscht.
Beispielaufgaben
Berechne die Umkehrfunktion:
1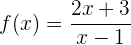
Wir tauschen mit
Wir eliminieren den Nenner
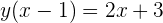
Wir lösen die Klammer auf
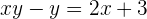
und bringen auf die andere Seite
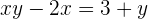
Wir klammen den gemeinsamten Faktor aus
und bestimmen nun
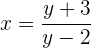
Wir tauschen x mit und erhalten die Umkehrfunktion
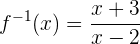
Wir überprüfen unser Ergebnis für 
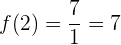
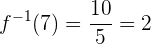
Da wir für 
erhalten und für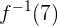 
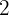, bedeutet dies, dass die Umkehrfunktion richtig ist
2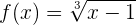
Wir tauschen mit
Wir nehmen beide Glieder hoch 3
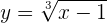
Wir bestimmen und tauschen mit
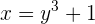
3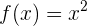
Wir tauschen mit
Wir bestimmen
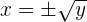
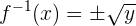
Hierbei handelt es sich nicht um eine Funktion.
Es existiert keine Umkehrfunktion, da jedes Element zwei Abbildungen hat. Eine Funktion kann jedoch höchstens eine Abbildung haben
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
