Kapitel
Die Ellipse ist der geometrische Ort der Punkte in der Ebene, deren Summe der Abstände zu zwei festen Punkten, den sogenannten Brennpunkten, konstant ist, d. h. 
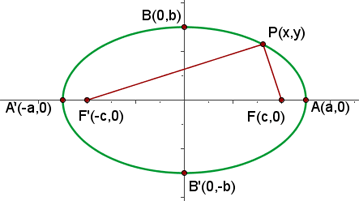
Die Gleichung einer Ellipse in Standarddarstellung hat die Form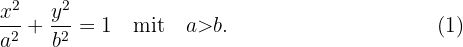
Die Gleichung (1) wird auch vereinfachte Gleichung der Ellipse mit horizontaler Achse genannt. Und wenn 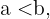 wird sie vereinfachte Gleichung der Ellipse mit vertikaler Achse genannt.
wird sie vereinfachte Gleichung der Ellipse mit vertikaler Achse genannt.
Wenn außerdem der Mittelpunkt der Ellipse nicht im Ursprung liegt, hat die Gleichung der Ellipse die Form 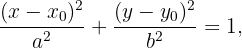
wobei der Punkt  dem Mittelpunkt dieser Ellipse entspricht. Wenn
dem Mittelpunkt dieser Ellipse entspricht. Wenn 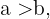 befindet sich die Ellipse in horizontaler Lage. Wenn
befindet sich die Ellipse in horizontaler Lage. Wenn 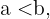 befindet sich die Ellipse in vertikaler Lage.
befindet sich die Ellipse in vertikaler Lage.

Elemente der Ellipse
1Brennpunkte: Dies sind die Fixpunkte  und
und 
2Brennachse: Die Gerade, die durch die Brennpunkte verläuft.
3Nebenachse: Die Mittelsenkrechte des Segments 
4Mittelpunkt: Der Punkt, in dem sich die Achsen schneiden. Er wird normalerweise mit  angegeben.
angegeben.
5Ortsvektoren: Die Segmente, die von einem Punkt der Ellipse zu den Brennpunkten verlaufen:  und
und 
6Brennstrecke: Das Segment  der Länge
der Länge  , wobei
, wobei  der Wert der halben Brennstrecke ist.
der Wert der halben Brennstrecke ist.
7Scheitelpunkte: Die Schnittpunkte der Ellipse mit den Achsen:  und
und 
8Hauptachse: Das Segment  der Länge
der Länge  , wobei
, wobei  der Wert der großen Halbachse ist.
der Wert der großen Halbachse ist.
9Nebenachse: Das Segment  der Länge
der Länge  , wobei
, wobei  der Wert der kleinen Halbachse ist.
der Wert der kleinen Halbachse ist.
10Symmetrieachsen: Die Geraden, die die große oder kleine Halbachse enthalten.
11Symmetriemittelpunkt: Fällt mit dem Mittelpunkt der Ellipse zusammen, der der Schnittpunkt der Symmetrieachsen ist.
Zusammenhang zwischen der Brennstrecke und den Halbachsen
Die Bedeutung der Größen  und
und  wird in der Abbildung 2 dargestellt. Wenn wir den Satz des Pythagoras anwenden, erhalten wir
wird in der Abbildung 2 dargestellt. Wenn wir den Satz des Pythagoras anwenden, erhalten wir 
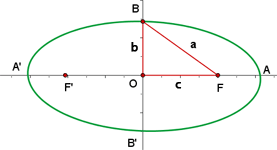
 und
und  einer Ellipse.
einer Ellipse.Exzentrizität der Ellipse
Die Exzentrizität ist eine Zahl, die die größere oder geringere Abflachung der Ellipse misst und dem Quotienten aus ihrer halben Brennstrecke und ihrer großen Halbachse entspricht, d. h. 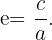
Da außerdem immer 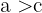 ist, gilt für die Exzentrizität
ist, gilt für die Exzentrizität 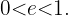
Beobachtungen: 1 Wenn die Exzentrizität einer Ellipse  wäre, hätten wir
wäre, hätten wir 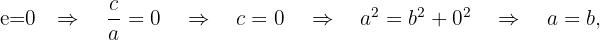
was bedeutet, dass die Brennpunkte gleich dem Mittelpunkt sind. Das heißt,
Daher hätten wir keine Ellipse, sondern einen Kreis mit dem Mittelpunkt 
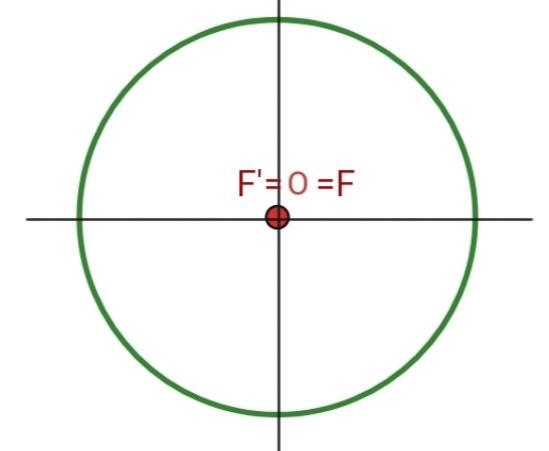
2 Wenn die Exzentrizität einer Ellipse  wäre, hätten wir
wäre, hätten wir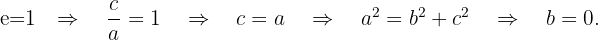
Wenn also  , können wir der Abbildung 2 entnehmen, dass wir nur die Brennachse haben. Das heißt, eine "Ellipse" mit der Exzentrizität
, können wir der Abbildung 2 entnehmen, dass wir nur die Brennachse haben. Das heißt, eine "Ellipse" mit der Exzentrizität 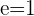 ist nur eine Gerade.
ist nur eine Gerade.
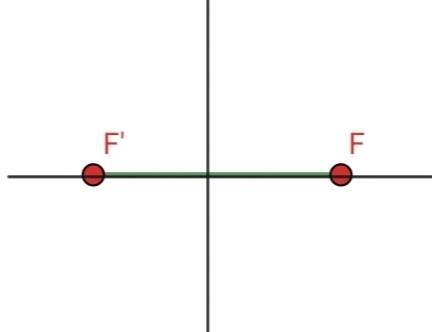
Im Folgenden werden einige Beispiele für Ellipsen mit unterschiedlichen Exzentrizitätswerten gezeigt:
1 Ellipse mit Exzentrizität 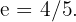
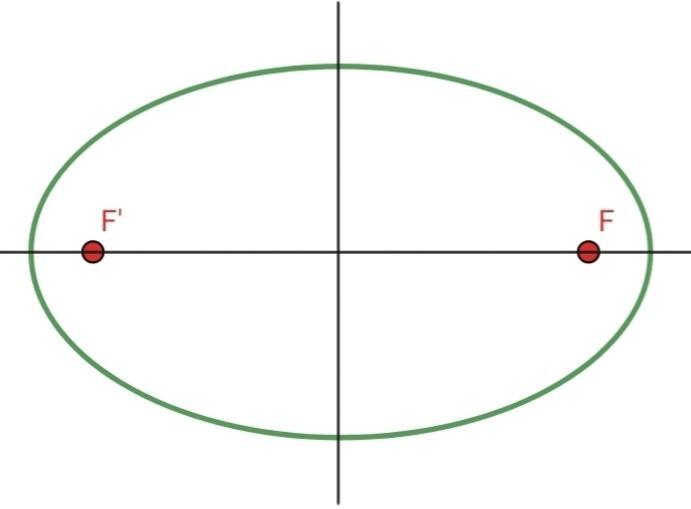
2 Ellipse mit Exzentrizität 
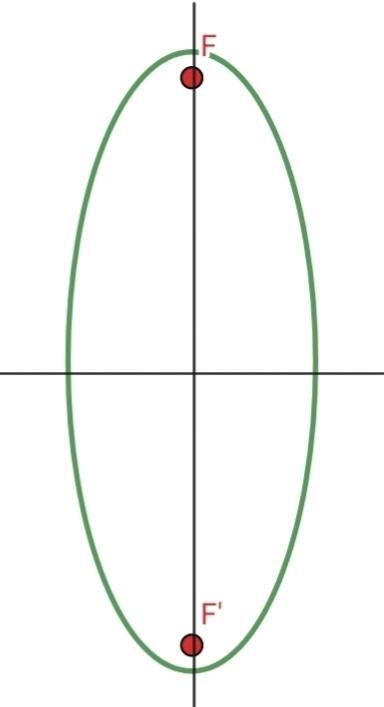
3 Ellipse mit Exzentrizität 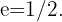
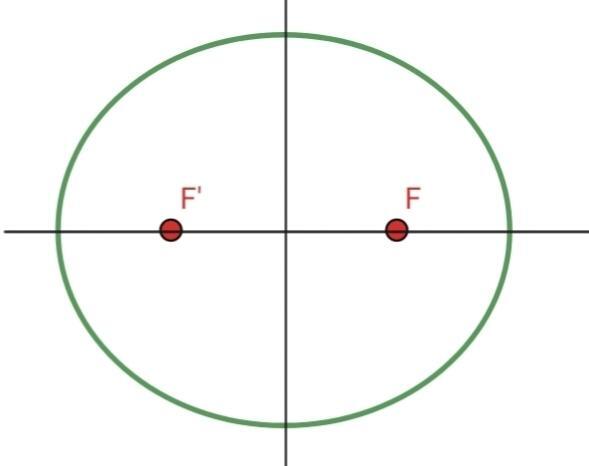
Mit KI zusammenfassen:












