Es ist der geometrische Ort der Punkte der Ebene, deren Summe der Abstände zu zwei Fixpunkten, den Brennpunkten, konstant ist.
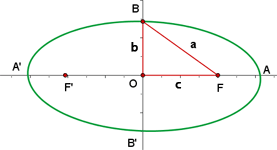
Elemente der Ellipse
1Brennpunkte: Dies sind die fixen Punkte 
und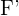 
.
2 Brennachse: Die Gerade, die durch die Brennpunkte verläuft.
3Halbachse: Mittelsenkrechte des Segments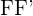 
.
4Mittelpunkt: Der Schnittpunkt der Achsen.
5Ortsvektoren: Dies sind die Segmente, die von einem Punkt der Ellipse zu den Brennpunkten gehen: 
und 
.
6Brennweite: Sie ist das Segment 
der Länge 
, 
ist der Wert der halben Brennweite.
7Scheitelpunkte: Die Schnittpunkte der Ellipse mit den Achsen: 
und 
.
8Hauptachse: Das Segment 
der Länge 
, wobei 
der Wert der größeren Halbachse ist.
9Nebenachse: Das Segment 
der Länge 
, wobei 
der Wert der kleineren Halbachse ist.
10Symmetrieachse: Dies sind die Geraden, die entweder die Hauptachse oder die Nebenachse enthalten.
11Symmetriemittelpunkt: Er fällt mit dem Mittelpunkt der Ellipse zusammen, der der Schnittpunkt der Symmetrieachsen ist.
Verhältnis zwischen der Brennweite und den Halbachsen
Sie ist gegeben durch:
Exzentrizität
Sie ist eine Zahl, die die größere oder kleinere Abflachung der Ellipse misst. Sie ist gleich dem Quotienten aus der halben Brennweite und der größeren Halbachse.
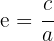
mit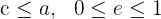 
Vereinfachte Gleichung
Wenn die Hauptachse auf der x-Achse liegt, erhalten wir folgende Gleichung:
Die Koordinaten der Brennpunkte si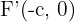nd:
und 
Ellipse mit Brennpunkten auf der y-Achse
Wenn die Hauptachse auf der x-Achse liegt, erhalten wir folgende Gleichung:
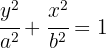
Die Koordinaten der Brennpunkte sind:
und 
Ellipse mit Achsen, die parallel zur x-Achse sind, und deren Mittelpunkt nicht im Ursprung liegt
Wenn der Mittelpunkt einer Ellipse 
ist und die Hauptachse parallel zur 
-Achse verläuft, haben die Brennpunkte die Koordinaten 
und 
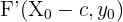. Die Gleichung dieser Ellipse lautet dann:
Wenn wir die Nenner entfernen und die Gleichungen ausformulieren, erhalten wir im Allgemeinen eine Gleichung der Form:
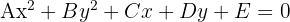
und 
haben dabei das gleiche Vorzeichen.
Ellipse mit einer Achse, die parallel zur y-Achse verläuft, und deren Mittelpunkt nicht im Ursprung liegt
Wenn der Mittelpunkt einer Ellipse ist und die Hauptachse parallel zur 
-Achse verläuft, haben die Brennpunkte die Koordinaten 
uns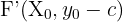 
. Die Gleichung dieser Ellipse lautet dann:
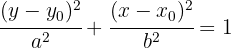
Wenn wir die Nenner entfernen und die Gleichungen ausformulieren, erhalten wir im Allgemeinen eine Gleichung der Form:
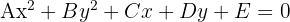
und haben dabei das gleiche Vorzeichen.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
