Sind der Mittelpunkt eine Ellipse  und ihre Hauptachse parallel zur Achse der Abszissen (Achse
und ihre Hauptachse parallel zur Achse der Abszissen (Achse  ), besitzen die Brennpunkte die Koordinaten
), besitzen die Brennpunkte die Koordinaten  und
und  . Die Ellipsengleichung lautet
. Die Ellipsengleichung lautet
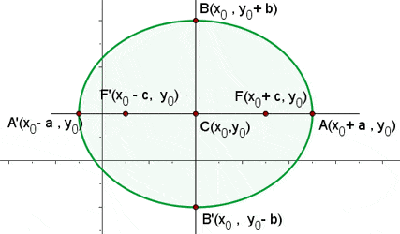

mit der entsprechenden großen und kleinen Halbachse  und
und  .
.
Durch Auflösen der Nenner und Vereinfachen der Gleichung erhält man in der Regel die Form:

 und
und  haben dabei dasselbe Vorzeichen. Diese Formel nennt man auch allgemeine Gleichung für Kegelschnitte.
haben dabei dasselbe Vorzeichen. Diese Formel nennt man auch allgemeine Gleichung für Kegelschnitte.
Beispiele
Stelle die Ellipsengleichung mit Brennpunkt  , Scheitelpunkt
, Scheitelpunkt  und Mittelpunkt
und Mittelpunkt  auf.
auf.
Zunächst ist festzustellen, dass die Hauptachse parallel zur Abszissenachse verläuft, was wir anhand des Mittelpunkts und eines der Brennpunkte feststellen können; beachte, dass der Brennpunkt rechts vom Mittelpunkt der Ellipse liegt. Dadurch erhalten wir vorerst die Gleichung

Wir wissen, dass  für die größere Halbachse steht. Die größere Halbachse ist gleich dem Abstand zwischen Mittelpunkt und Scheitelpunkt.
für die größere Halbachse steht. Die größere Halbachse ist gleich dem Abstand zwischen Mittelpunkt und Scheitelpunkt.

Außerdem wissen wir, dass für die kleine Halbachse  gilt, wobei
gilt, wobei  den Abstand vom Mittelpunkt der Ellipse zum Brennpunkt ist, das heißt
den Abstand vom Mittelpunkt der Ellipse zum Brennpunkt ist, das heißt

Somit ist

Wir erhalten die Gleichung

Gegeben sei eine Ellipse mit der Gleichung

Ermittle ihren Mittelpunkt, Halbachsen, Scheitelpunkte und Brennpunkte.
An der Ellipsengleichung lässt sich ablesen, dass der Mittelpunkt  ist.
ist.
Um die Halbachsen zu finden, stellen wir fest, dass wir  aus
aus 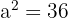 und
und  , also
, also  erhalten.
erhalten.  ist die größere Halbachse, da der Wert größer als der von
ist die größere Halbachse, da der Wert größer als der von  ist. Im Umkehrschluss ist
ist. Im Umkehrschluss ist  die kleine Halbachse.
die kleine Halbachse.
Da  die größere Halbachse darstellt und der Teiler des Ausdrucks
die größere Halbachse darstellt und der Teiler des Ausdrucks  ist, ist die große Halbachse parallel zur Abszissenachse. Damit liegt der Scheitelpunkt
ist, ist die große Halbachse parallel zur Abszissenachse. Damit liegt der Scheitelpunkt  Einheiten rechts und
Einheiten rechts und  Einheiten links des Mittelpunkts. Die Scheitelpunkte sind also
Einheiten links des Mittelpunkts. Die Scheitelpunkte sind also  und
und  .
.
Als Letztes müssen die Brennpunkte gefunden werden. Die Hälfte der Brennweite (Abstand vom Mittelpunkt zu jedem der Brennpunkte) wird mit  ausgedrückt und erfüllt
ausgedrückt und erfüllt  . Man erhält also
. Man erhält also
 .
.
Man erhält  und die Brennpunkte
und die Brennpunkte  und
und  .
.

Ellipse in 1. Hauptlage
Wir nehmen den Mittelpunkt der Koordinaten als Mittelpunkt der Ellipse und die Koordinatenachsen als Achsen der Ellipse. Die Koordinaten der Brennpunkte sind:

 und
und  . Außerdem trifft auf jeden beliebigen Punkt
. Außerdem trifft auf jeden beliebigen Punkt
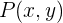
auf der Ellipse zu, dass
 .
.
Man erkennt, dass dieser Ausdruck gleichwertig zu
 ist.
ist.
Durch Vereinfachen und Auflösen, erhält man
 .
.
mit  , wie auf der vorherigen Grafik zu sehen ist.
, wie auf der vorherigen Grafik zu sehen ist.
Beispiel:
Finde die charakteristischen Elemente und die Ellipsengleichung für die Ellipse in 1. Hauptlage mit den Brennpunkten:  ,
,  und großer Halbachse
und großer Halbachse  .
.
Zu unserer Aufgabe gehört folgende Grafik
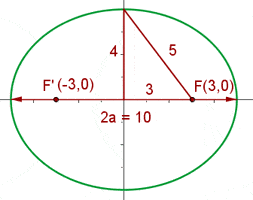
Man sieht, dass der Mittelpunkt der Ellipse auch der Mittelpunkt der beiden Brennpunkte ist, das heißt

Die Brennpunkte liegen auf der Abszissenachse, folglich liegt dort auch die große Halbachse.  ist die Hälfte der großen Halbachse, d.h.
ist die Hälfte der großen Halbachse, d.h.  mit
mit  als große Halbachse.
als große Halbachse.
Die Hälfte der Brennweite  ist gleich dem Abstand von den Brennpunkten zum Mittelpunkt der Ellipse
ist gleich dem Abstand von den Brennpunkten zum Mittelpunkt der Ellipse  .
.
Zuletzt findet man die kleine Halbachse anhand der großen Halbachse und  , wenn für die kleine Halbachse
, wenn für die kleine Halbachse  zutrifft:
zutrifft:

Man erhält  . Unsere Ellipsengleichung ist daher
. Unsere Ellipsengleichung ist daher
 .
.
Ellipse in 2. Hauptlage
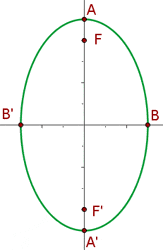
Wenn die Hauptachse auf der y-Achse des Koordinatensystems verläuft, folgt die Berechnung dieser Gleichung:

Die Koordinaten der Brennpunkte sind  y
y  .
.
Beispiel
Gegegeben ist die Ellipsengleichung

Finde die Koordinaten der Scheitelpunkte, der Brennpunkte und die Exzentrität der Ellipse (= Abstand des Brennpunktes zum Mittelpunkt)
Ermittle zuerst die Hälfte der Brennweite. Die Hälfte der Brennweite wird mit  bezeichnet und es gilt
bezeichnet und es gilt  , das heißt
, das heißt
 ,
,
Somit ist  . Aus diesem Wert können wir schließen, dass die Brennpunkte die Koordinaten
. Aus diesem Wert können wir schließen, dass die Brennpunkte die Koordinaten  und
und  haben.
haben.
Um die Scheitelpunkte zu ermitteln, erinnere dich daran, dass diese sich a  Einheiten über und unter dem Mittelpunkt der Ellipse befinden, das heißt für
Einheiten über und unter dem Mittelpunkt der Ellipse befinden, das heißt für  erhält man die Scheitelpunkte
erhält man die Scheitelpunkte  und
und  .
.
Die Exzentrität der Ellipse ist gleich
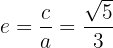 .
.
Hauptachsentransformation
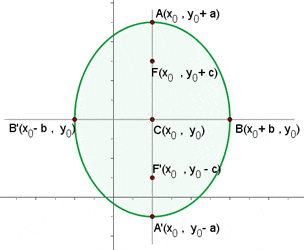
Wenn der Mittelpunkt einer Ellipse  ist (sei er der Ursprungspunkt oder nicht) und die Hauptachse parallel zur y-Achse des Koordinatensystems verläuft, haben die Brennpunkte die Koordinaten
ist (sei er der Ursprungspunkt oder nicht) und die Hauptachse parallel zur y-Achse des Koordinatensystems verläuft, haben die Brennpunkte die Koordinaten  und
und  und die Ellipsengleichung ist:
und die Ellipsengleichung ist:

Beispiele
Schreibe dir folgenden Gleichungen in die allgemeine Kegelschnittgleichung (oder die allgemeine Ellipsengleichung) um und ermittle die Koordinaten ihrer Brennpunkte, Scheitelpunkte sowie ihre Exzentrität und stelle sie grafisch dar.
a. 
b. 
c. 
d. 
a. 
Um die Ellipsengleichung zu erhalten, müssen die grundlegenden Regeln der Algebra angewandt werden

Die letzte Gleichung enspricht bereits in ihrer Form der Ellipsengleichung. An ihr lässt sich ablesen, dass der Mittelpunkt der Ellipse  ist.
ist.
Man erkennt ebenso, dass die große Halbachse  ist und die kleine Halbachse
ist und die kleine Halbachse  . Da die große Halbachse den Term der
. Da die große Halbachse den Term der  teilt, muss die Hauptachse der Ellipse parallel zur Abszissenachse liegen. Die Scheitelpunkte liegen daher
teilt, muss die Hauptachse der Ellipse parallel zur Abszissenachse liegen. Die Scheitelpunkte liegen daher  Einheiten rechts und links vom Mittelpunkt der Ellipse und haben die Koordinaten
Einheiten rechts und links vom Mittelpunkt der Ellipse und haben die Koordinaten  und
und  .
.
Um die Brennpunkte zu erhalten, muss die Hälfte der Brennweite  berechnet werden, für die gilt
berechnet werden, für die gilt  , d.h. wir erhalten
, d.h. wir erhalten

Folglich ist  . Die Brennpunkte liegen
. Die Brennpunkte liegen  Einheiten links und rechts des Mittelpunkts der Ellipse und haben daher die Koordinaten
Einheiten links und rechts des Mittelpunkts der Ellipse und haben daher die Koordinaten  und
und  .
.
Die Exzentrität ist durch

gegeben.
Die grafische Darstellung der Ellipse sieht wie folgt aus:
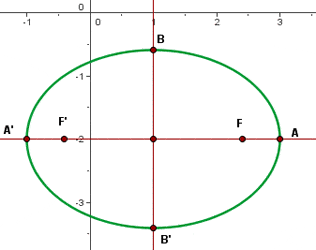
b. 
Um die Ellipsengleichung zu erhalten, müssen die grundlegenden Regeln der Algebra angewandt werden

Die letzte Gleichung enspricht bereits in ihrer Form der Ellipsengleichung. Anhand der Gleichung lässt sich erkennen, dass der Mittelpunkt der Ellipse bei  liegt.
liegt.
Aus der Gleichung lässt sich auch ablesen, dass die große Halbachse  und die kleine Halbachse
und die kleine Halbachse  ist. Da die große Halbachse den Term der
ist. Da die große Halbachse den Term der  teilt, muss die Hauptachse der Ellipse parallel zur Koordinatenachse liegen. Die Scheitelpunkte liegen daher
teilt, muss die Hauptachse der Ellipse parallel zur Koordinatenachse liegen. Die Scheitelpunkte liegen daher  Einheiten rechts und links vom Mittelpunkt der Ellipse und haben die Koordinaten
Einheiten rechts und links vom Mittelpunkt der Ellipse und haben die Koordinaten  und
und  .
.
Um die Brennpunkte zu erhalten, muss die Hälfte der Brennweite  berechnet werden, für die gilt
berechnet werden, für die gilt  , d.h. wir erhalten
, d.h. wir erhalten

Aus der letzten Gleichung ergibt sich  . Die Brennpunkte liegen
. Die Brennpunkte liegen  Einheiten links und rechts des Mittelpunkts der Ellipse und haben daher die Koordinaten
Einheiten links und rechts des Mittelpunkts der Ellipse und haben daher die Koordinaten  und
und  .
.
Die Exzentrität ist durch

Die grafische Darstellung der Ellipse sieht wie folgt aus:
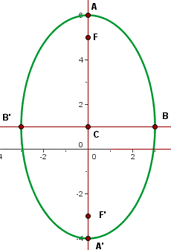
c. 
Um die Ellipsengleichung zu erhalten, müssen die grundlegenden Regeln der Algebra angewandt werden

Die letzte Gleichung enspricht bereits in ihrer Form der Ellipsengleichung. Anhand der Gleichung lässt sich erkennen, dass der Mittelpunkt der Ellipse bei  liegt.
liegt.
Aus der Gleichung lässt sich auch ablesen, dass die große Halbachse  und die kleine Halbachse
und die kleine Halbachse  ist. Da die große Halbachse den Term der
ist. Da die große Halbachse den Term der  teilt, muss die Hauptachse der Ellipse parallel zur Abszissenachse liegen. Daraus lässt sich schließen, dass die Scheitelpunkte
teilt, muss die Hauptachse der Ellipse parallel zur Abszissenachse liegen. Daraus lässt sich schließen, dass die Scheitelpunkte  Einheiten rechts und links vom Mittelpunkt der Ellipse liegen und die Koordinaten
Einheiten rechts und links vom Mittelpunkt der Ellipse liegen und die Koordinaten  und
und  besitzen.
besitzen.
Um die Brennpunkte zu erhalten, muss die Hälfte der Brennweite  berechnet werden, für die gilt
berechnet werden, für die gilt  , d.h. wir erhalten
, d.h. wir erhalten

Aus der letzten Gleichung ergibt sich  . Die Brennpunkte liegen
. Die Brennpunkte liegen  Einheiten links und rechts des Mittelpunkts der Ellipse und haben daher die Koordinaten
Einheiten links und rechts des Mittelpunkts der Ellipse und haben daher die Koordinaten  und
und  .
.
Die Exzentrität ist durch

Die grafische Darstellung der Ellipse sieht wie folgt aus:
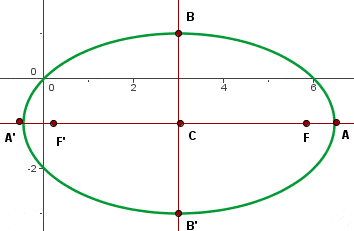
d. 
Um die Ellipsengleichung zu erhalten, müssen die grundlegenden Regeln der Algebra angewandt werden

Die letzte Gleichung enspricht bereits in ihrer Form der Ellipsengleichung. An ihr lässt sich ablesen, dass der Mittelpunkt der Ellipse  ist.
ist.
Man erkennt ebenso, dass die große Halbachse  ist und die kleine Halbachse
ist und die kleine Halbachse  . Da die große Halbachse den Term der
. Da die große Halbachse den Term der  teilt, muss die Hauptachse der Ellipse parallel zur Koordinatenachse liegen. Die Scheitelpunkte liegen daher
teilt, muss die Hauptachse der Ellipse parallel zur Koordinatenachse liegen. Die Scheitelpunkte liegen daher  Einheiten rechts und links vom Mittelpunkt der Ellipse und haben die Koordinaten
Einheiten rechts und links vom Mittelpunkt der Ellipse und haben die Koordinaten  und
und  .
.
Um die Brennpunkte zu erhalten, muss die Hälfte der Brennweite  berechnet werden, für die gilt
berechnet werden, für die gilt  , d.h. wir erhalten
, d.h. wir erhalten

Aus der letzten Gleichung ergibt sich  . Die Brennpunkte liegen
. Die Brennpunkte liegen  Einheiten links und rechts des Mittelpunkts der Ellipse und haben daher die Koordinaten
Einheiten links und rechts des Mittelpunkts der Ellipse und haben daher die Koordinaten  y
y  .
.
Die Exzentrität ist durch

Die grafische Darstellung der Ellipse sieht wie folgt aus:
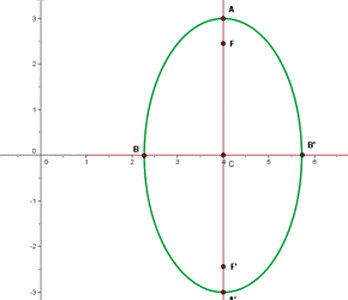
Stelle die Ellipsengleichung anhand der folgenden Vorgaben auf:
a. 
b. 
c. 
d. 
a. 
Beim Lösen der Gleichung fällt auf, dass man den Abstand  zwischen Brennpunkt und Mittelpunkt (=die Hälfte der Brennweite) leicht mit dem Wert
zwischen Brennpunkt und Mittelpunkt (=die Hälfte der Brennweite) leicht mit dem Wert  ablesen kann. Auch die große Halbachse ist leicht zu erhalten, da sie aus dem Abstand von Scheitelpunkt und Mittelpunkt gebildet wird und folglich
ablesen kann. Auch die große Halbachse ist leicht zu erhalten, da sie aus dem Abstand von Scheitelpunkt und Mittelpunkt gebildet wird und folglich  ist. Zuletzt kann die kleine Halbachse auf Basis der großen Halbachse und der Brennweite bestimmt werden, da
ist. Zuletzt kann die kleine Halbachse auf Basis der großen Halbachse und der Brennweite bestimmt werden, da  gilt, das heißt
gilt, das heißt

Folglich ist  . Wenn die Brennpunkte rechts und links des Mittelpunkts der Ellipse liegen, wird der Term, der
. Wenn die Brennpunkte rechts und links des Mittelpunkts der Ellipse liegen, wird der Term, der  enthält durch das Quadrat der großen Halbachse geteilt. Andersherum wird
enthält durch das Quadrat der großen Halbachse geteilt. Andersherum wird  durch das Quadrat der großen Halbachse geteilt, wenn die Brennpunkte über und unter dem Mittelpunkt liegen. Unsere Gleichung ist
durch das Quadrat der großen Halbachse geteilt, wenn die Brennpunkte über und unter dem Mittelpunkt liegen. Unsere Gleichung ist
 .
.
b. 
Beim Lösen der Gleichung fällt auf, dass man den Abstand  zwischen Brennpunkt und Mittelpunkt (=die Hälfte der Brennweite) leicht mit dem Wert
zwischen Brennpunkt und Mittelpunkt (=die Hälfte der Brennweite) leicht mit dem Wert  ablesen kann. Auch die große Halbachse ist leicht zu erhalten, da sie aus dem Abstand von Scheitelpunkt und Mittelpunkt gebildet wird und folglich
ablesen kann. Auch die große Halbachse ist leicht zu erhalten, da sie aus dem Abstand von Scheitelpunkt und Mittelpunkt gebildet wird und folglich  ist. Zuletzt kann die kleine Halbachse auf Basis der großen Halbachse und der Brennweite bestimmt werden, da
ist. Zuletzt kann die kleine Halbachse auf Basis der großen Halbachse und der Brennweite bestimmt werden, da  gilt, das heißt
gilt, das heißt

Folglich ist  . Wenn die Brennpunkte rechts und links des Mittelpunkts der Ellipse liegen, wird der Term, der
. Wenn die Brennpunkte rechts und links des Mittelpunkts der Ellipse liegen, wird der Term, der  enthält durch das Quadrat der großen Halbachse geteilt. Andersherum wird
enthält durch das Quadrat der großen Halbachse geteilt. Andersherum wird  durch das Quadrat der großen Halbachse geteilt, wenn die Brennpunkte über und unter dem Mittelpunkt liegen. Unsere Gleichung ist
durch das Quadrat der großen Halbachse geteilt, wenn die Brennpunkte über und unter dem Mittelpunkt liegen. Unsere Gleichung ist
 .
.
c. 
Beim Lösen der Gleichung fällt auf, dass man den Abstand  zwischen Brennpunkt und Mittelpunkt (=die Hälfte der Brennweite) leicht mit dem Wert
zwischen Brennpunkt und Mittelpunkt (=die Hälfte der Brennweite) leicht mit dem Wert  ablesen kann. Auch die große Halbachse ist leicht zu erhalten, da sie aus dem Abstand von Scheitelpunkt und Mittelpunkt gebildet wird und folglich
ablesen kann. Auch die große Halbachse ist leicht zu erhalten, da sie aus dem Abstand von Scheitelpunkt und Mittelpunkt gebildet wird und folglich  ist. Zuletzt kann die kleine Halbachse auf Basis der großen Halbachse und der Brennweite bestimmt werden, da
ist. Zuletzt kann die kleine Halbachse auf Basis der großen Halbachse und der Brennweite bestimmt werden, da  gilt, das heißt
gilt, das heißt

Folglich ist  . Wenn die Brennpunkte rechts und links des Mittelpunkts der Ellipse liegen, wird der Term, der
. Wenn die Brennpunkte rechts und links des Mittelpunkts der Ellipse liegen, wird der Term, der  enthält durch das Quadrat der großen Halbachse geteilt. Andersherum wird
enthält durch das Quadrat der großen Halbachse geteilt. Andersherum wird  durch das Quadrat der großen Halbachse geteilt, wenn die Brennpunkte über und unter dem Mittelpunkt liegen. Unsere Gleichung ist
durch das Quadrat der großen Halbachse geteilt, wenn die Brennpunkte über und unter dem Mittelpunkt liegen. Unsere Gleichung ist
 .
.
d. 
Beim Lösen der Gleichung fällt auf, dass man den Abstand  zwischen Brennpunkt und Mittelpunkt (=die Hälfte der Brennweite) leicht mit dem Wert
zwischen Brennpunkt und Mittelpunkt (=die Hälfte der Brennweite) leicht mit dem Wert  ablesen kann. Auch die große Halbachse ist leicht zu erhalten, da sie aus dem Abstand von Scheitelpunkt und Mittelpunkt gebildet wird und folglich
ablesen kann. Auch die große Halbachse ist leicht zu erhalten, da sie aus dem Abstand von Scheitelpunkt und Mittelpunkt gebildet wird und folglich  ist. Zuletzt kann die kleine Halbachse auf Basis der großen Halbachse und der Brennweite bestimmt werden, da
ist. Zuletzt kann die kleine Halbachse auf Basis der großen Halbachse und der Brennweite bestimmt werden, da  gilt, das heißt
gilt, das heißt

Folglich ist  . Wenn die Brennpunkte rechts und links des Mittelpunkts der Ellipse liegen, wird der Term, der
. Wenn die Brennpunkte rechts und links des Mittelpunkts der Ellipse liegen, wird der Term, der  enthält durch das Quadrat der großen Halbachse geteilt. Andersherum wird
enthält durch das Quadrat der großen Halbachse geteilt. Andersherum wird  durch das Quadrat der großen Halbachse geteilt, wenn die Brennpunkte über und unter dem Mittelpunkt liegen. Unsere Gleichung ist
durch das Quadrat der großen Halbachse geteilt, wenn die Brennpunkte über und unter dem Mittelpunkt liegen. Unsere Gleichung ist
 .
.
Stelle die Ellipsengleichung für eine Ellipse auf, die durch den Punkt  verläuft, deren Mittelpunkt gleich dem Ursprungspunkt ist und deren kleine Halbachse parallel zur Koordinatenachse verläuft und
verläuft, deren Mittelpunkt gleich dem Ursprungspunkt ist und deren kleine Halbachse parallel zur Koordinatenachse verläuft und  misst.
misst.
Die Tatsache, dass die kleine Halbachse  misst, lässt schließen, dass
misst, lässt schließen, dass  ist. Die Ellipse verläuft durch den Punkt
ist. Die Ellipse verläuft durch den Punkt  , das heißt für
, das heißt für  und
und  ist die Ellipsengleichung gültig. Beim Einsetzen dieses Punktes und des Werts von
ist die Ellipsengleichung gültig. Beim Einsetzen dieses Punktes und des Werts von  muss nur nach
muss nur nach  aufgelöst werden
aufgelöst werden

Unsere Gleichung ist

Wir wissen, dass der Mittelpunkt einer Ellipse im Ursprungspunkt liegt und die Hälfte ihrer Brennweite  beträgt. Ein Punkt der Ellipse ist von ihren Brennpunkten 2 und 6 Einheiten entfernt. Stelle die Ellipsengleichung dieser Ellipse auf und nimm dabei an, dass ihre große Halbachse entlang der Koordinatenachse verläuft.
beträgt. Ein Punkt der Ellipse ist von ihren Brennpunkten 2 und 6 Einheiten entfernt. Stelle die Ellipsengleichung dieser Ellipse auf und nimm dabei an, dass ihre große Halbachse entlang der Koordinatenachse verläuft.
Die Tatsache, dass die Hälfte der Brennweite  beträgt, lässt uns schließen, dass
beträgt, lässt uns schließen, dass  , also
, also  ist. Die Summe der Abstände der Brennpunkte zu einem Punkt auf der Ellipse beträgt immer
ist. Die Summe der Abstände der Brennpunkte zu einem Punkt auf der Ellipse beträgt immer  , folglich ist
, folglich ist

Anhand von  und
und  lässt sich nun auch
lässt sich nun auch  berechnen
berechnen

Da sich die große Halbachse auf der Koordinatenachse befindet, ist für die Gleichung folgendes gegeben

Stelle die Ellipsengleichung für eine Ellipse auf, derenBrennweite  beträgt und deren einbeschriebenes Rechteck einen Flächeninhalt von
beträgt und deren einbeschriebenes Rechteck einen Flächeninhalt von  aufweist. Die große Halbachse der Ellipse verläuft parallel zur Abszissenachse.
aufweist. Die große Halbachse der Ellipse verläuft parallel zur Abszissenachse.
Analysiere zuerst die Daten, die bereits gegeben sind: die Brennweite ist  , das heißt
, das heißt  und folglich ist
und folglich ist  .
.
Die Fläche des einbeschriebenen Rechtecks misst  und ist gleich dem Produkt aus kleiner und großer Halbachse, da diese den Seitenlängen des Rechtecks entsprechen. Die große Halbachse misst
und ist gleich dem Produkt aus kleiner und großer Halbachse, da diese den Seitenlängen des Rechtecks entsprechen. Die große Halbachse misst  und die kleine Halbachse
und die kleine Halbachse  , woraus sich
, woraus sich  ergibt. Nun kann man mithilfe des Einsatzverfahrens nach einer Variablen auflösen. Wir lösen nach
ergibt. Nun kann man mithilfe des Einsatzverfahrens nach einer Variablen auflösen. Wir lösen nach  auf:
auf:  .
.
Wir kennen ebenso die Beziehung  und kennen bereits den Wert von
und kennen bereits den Wert von  und von
und von  . Durch Einsetzen dieser beiden Werte in die erste Gleichung erhalten wir den Wert von
. Durch Einsetzen dieser beiden Werte in die erste Gleichung erhalten wir den Wert von  .
.

Die Wurzeln des ermittelten Polynoms sind  . Da
. Da  eine reelle positive Zahl sein muss, ist die einzig mögliche Lösung
eine reelle positive Zahl sein muss, ist die einzig mögliche Lösung  . Durch Einsetzen dieser Werte in die erste Gleichung erhalten wir den Wert von
. Durch Einsetzen dieser Werte in die erste Gleichung erhalten wir den Wert von  . Diesen setzen wir in die Gleichung
. Diesen setzen wir in die Gleichung  ein und erhalten
ein und erhalten  . Da die Werte der Halbachsen schon feststehen, stellen wir nun die Gleichung auf. Die Hauptachse der Ellipse liegt auf der Abszissenachse, daher muss der Wert, der die
. Da die Werte der Halbachsen schon feststehen, stellen wir nun die Gleichung auf. Die Hauptachse der Ellipse liegt auf der Abszissenachse, daher muss der Wert, der die  erhält durch das Quadrat der großen Halbachse geteilt werden
erhält durch das Quadrat der großen Halbachse geteilt werden

Stelle die Ellipsengleichung für eine Ellipse auf, in der einer der beiden Scheitelpunkte  einheiten vom einen Brennpunkt und
einheiten vom einen Brennpunkt und  vom anderen entfernt ist. Der Einfachheit halber nehmen wir an, dass der Mittelpunkt gleich dem Ursprungspunkt der Ellipse ist und dass ihre große Halbachse auf der Abszissenachse verläuft.
vom anderen entfernt ist. Der Einfachheit halber nehmen wir an, dass der Mittelpunkt gleich dem Ursprungspunkt der Ellipse ist und dass ihre große Halbachse auf der Abszissenachse verläuft.
Die folgende Garfik hilft uns, die genannten Abstände besser zu verstehen und wie man basierend darauf  und
und  berechnen kann, um schließlich
berechnen kann, um schließlich  zu erhalten.
zu erhalten.
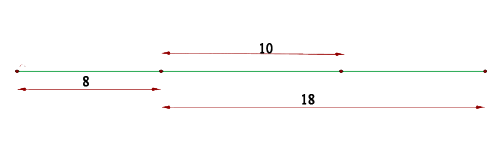
Der Abstand vom Scheitelpunkt zum entferntesten Brennpunkt beträgt  , während der kürzeste Abstand
, während der kürzeste Abstand  beträgt. Zieht man den kleineren Abstand zum Brennpunkt vom größeren ab, erhält man die Brennweite, das heißt
beträgt. Zieht man den kleineren Abstand zum Brennpunkt vom größeren ab, erhält man die Brennweite, das heißt  , bzw.
, bzw.  . Addiert man zum Abstand des Scheitelpunkts zum entferntesten Brennpunkt den Abstand zum naheliegendsten Brennpunkt, erhält man den Abstand eines Scheitelpunkts vom anderen:
. Addiert man zum Abstand des Scheitelpunkts zum entferntesten Brennpunkt den Abstand zum naheliegendsten Brennpunkt, erhält man den Abstand eines Scheitelpunkts vom anderen:  , bzw.
, bzw.  . Anhand dieser Werte kann das Quadrat der kleinen Halbachse berechnet werden, da
. Anhand dieser Werte kann das Quadrat der kleinen Halbachse berechnet werden, da
 .
.
Unsere Gleichung ist also
 .
.
Stelle die Ellipsengleichung für eine Ellipse auf, die durch den Punkt  verläuft und deren Exzentizität
verläuft und deren Exzentizität  ist. Der Einfachheit halber nehmen wir an, dass der Mittelpunkt gleich dem Ursprungspunkt der Ellipse ist und dass ihre große Halbachse auf der Abszissenachse verläuft.
ist. Der Einfachheit halber nehmen wir an, dass der Mittelpunkt gleich dem Ursprungspunkt der Ellipse ist und dass ihre große Halbachse auf der Abszissenachse verläuft.
Die Exzentrizität ist  . Vereinfache die Gleichung und du erhältst
. Vereinfache die Gleichung und du erhältst  . Da die Ellipse durch den Punkt
. Da die Ellipse durch den Punkt  verläuft, erhalten wir für diesen Wert ein Ergebnis der Ellipsengleichung
verläuft, erhalten wir für diesen Wert ein Ergebnis der Ellipsengleichung

Wir haben bereits den Wert von  und
und  ermittelt und wissen außerdem
ermittelt und wissen außerdem  . Setze die Werte von
. Setze die Werte von  und
und  ein, um
ein, um  zu erhalten.
zu erhalten.
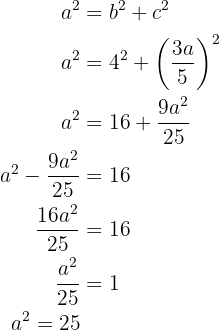
Unsere Gleichung ist

Mit KI zusammenfassen:













