Kapitel
Definition
Bei einer Exponentialfunktion wird jedem reelen Wert von 
eine Potenz 
zugeordnet. Dabei ist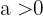 
und 
. Die Funktion hat die Form:
Die Zahl 
wird auch als Basis bezeichnet.
Grafische Darstellungen von Exponentialfunktionen
Wie verhält sich die Exponentialfunktion im Bezug auf ihre Basis?
Wir erstellen eine Wertetabelle für die Funktion 
|  |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
Wir zeichnen den Graphen ins Koordinatensystem ein
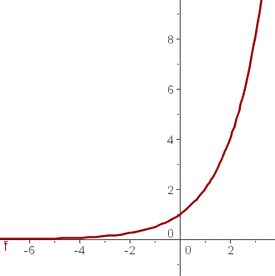
Zum Vergleich erstellen wir eine Wertetabelle für die Funktion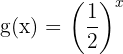 
|  |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |
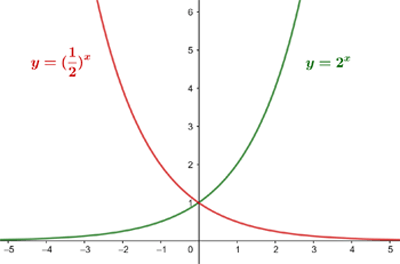
Wir zeichnen den Graphen ins Koordinatensystem ein
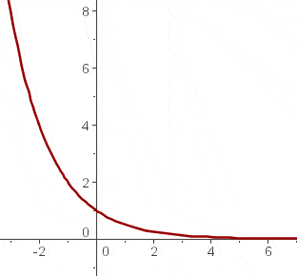
Man kann erkennen, dass die erste Funktion konstant ansteigt, während die zweite konstant abnimmt. Beide Graphen sind symmetrisch zur 
-Achse
Natürliche Exponentialfunktion
Die natürliche Exponentialfunktion (auch e-Funktion genannt) hat die Form 
. Dabei ist 
durch
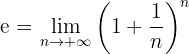festgelegt.
Diese Schreibweise wurde um 1730 von Leonhard Euler eingeführt, der die Eigenschaften der Zahl erforschte. Die Zahl ist eine irrationale Zahl. Ihre ersten 10 Dezimalstellen sind 
.
Eigenschaften der e-Funktion
1 Definitionsbereich: 
(reelle positive Zahlen).
2 Verlauf: 
.
3 Die Funktion ist stetig.
4Die Punkte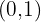 
und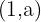 
sind Teil des Graphen.
5 Die Funktion ist injektiv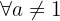 
(kein Bild besitzt mehr als ein Urbild).
6 Die Funktion ist steigend, wenn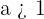 
.
7 Die Funktion ist fallend, wenn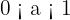 
.
8 Die Funktionskurven und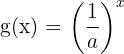 
sind im Bezug zur -Achse symmetrisch.
9 Die Exponentialfunktion mit 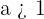steigt für jeden Wert von 
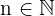schneller an als die Potenzfunktion 
.
10 Die Exponentialfunktion hat die Umkehrfunktion 
. Die Umkehrfunktion der e-Funktion ist 
.
Anwendungsbeispiele der Exponentialfunktion
Exponentialfunktionen finden in einer Vielzahl von Arbeitsbereichen Anwendung, zum Beispiel zur Berechnung des Bevölkerungswachstums und der Zinssätze.
Exponentielles Wachstum und Verfall
Um das Wachstum einer Bevölkerung zu beschreiben, wird die folgende Formel verwendet:
Die Funktion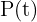 
steigt exponentiell an und stellt die Größe der Bevölkerung zu einem Zeitpunkt 
dar; 
ist die Konstante, die das Wachstum bzw. den Verfall anzeigt; wenn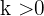 
, wird sie als Wochstumskonstante bezeichnet. Wenn 
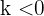, bezeichnet man sie als Verfallskonstante. 
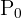stellt die ursprüngliche Bevölkerung zum Zeitpunkt des Beginns der Aufzeichnung dar: 
.
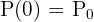Die vorherige Formel wird auf Basis der e-Funktion dargestellt. In manchen Fällen kann sie auch als Funktion mit Basis ausgedrückt werden: dafür werden einfach die Eigenschaften der Exponenten auf 
angewandt und a als 
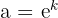ausgedrückt. Man erhält:
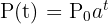
Beispiel: Eine Forschungsgruppe untersucht eine Bakterienkultur. Zum Startzeitpunkt der Untersuchung liegen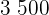 
Bakterien vor; eine halbe Stunde später bereits 
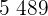. Bestimme:
1 Die Anzahl der Bakterien nach 2 Stunden.
2 Die Anzahl der Bakterien nach 3 Stunden.
3 Die durchschnittliche Zunahme-Rate der Bakterienzahl innerhalb der zweiten Stunde.
4 Die Zeit, in der sich die Bakterienzahl verdoppelt hat.
5 Die Zeit, in der die Bakterienzahl bei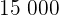 
liegen wird.
Um die Aufgaben lösen zu können, müssen wir die Wachstumsformel mit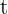 
in Minuten ausdrücken.
Wir kennen bereits die Anfangszahl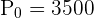 
, aber die Wachstumskonstante ist noch unbekannt. Um den Wert von 
zu finden, verwenden wir die Information aus der Aufgabenstellung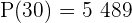 
in der Wachstumsformel:
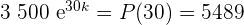
Wir teilen beide Seiten durch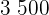 
und wenden die Kehrfunktion der e-Funktion an:
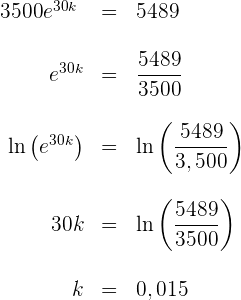
Die Funktion, die das Wachstum der Bakterienzahl beschreibt, ist also:
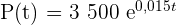
1 Die Anzahl der Bakterien nach 2 Stunden beträgt:
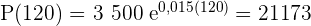
2 Die Anzahl der Bakterien nach 3 Stunden beträgt:
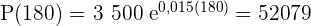
3 Die durchschnittliche Zunahme-Rate der Bakterienzahl innerhalb der zweiten Stunde beträgt:
In der zweiten Stunde der Untersuchung, d.h. zwischen 
und 
, verändert sich die Bakterienzahl um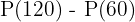 
, daher beträgt die durchschnittliche Zunahme während dieser Zeit
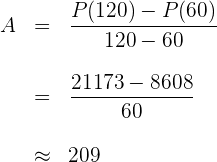
Die Bakterienzahl wächst in der zweiten Stunde der Messung im Durchschnitt um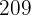 
Bakterien pro Minute.
4 Die Zeit, in der sich die Bakterienzahl verdoppelt hat, beträgt:
Wende hierfür folgende Gleichung an:
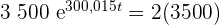
Wir teilen beide Seiten durch 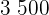und wenden die Kehrfunktion der e-Funktion an:
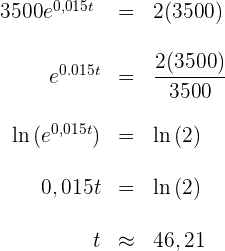
Die Bakterienzahl verdoppelt sich also innerhalb von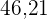 
Minuten.
5 Die Zeit, in der die Bakterienzahl bei 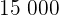liegen wird.
Wende hierfür folgende Gleichung an:
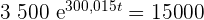
Wir teilen beide Seiten durch 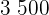und wenden die Kehrfunktion der e-Funktion an:
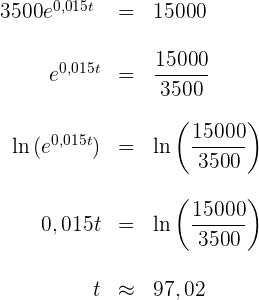
Die Bakterienzahl liegt nach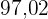 
Minuten bei 
.
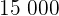Unterjährige Verzinsung
Ein anfänglicher Geldbetrag 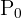wird zu einem Zinssatz 
verzinst, der in Dezimalzahlen angegeben wird. Wenn die Zinsen nur einmal berechnet werden, ergibt sich nach Hinzurechnen der Zinsen ein Endbetrag 
von
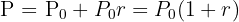
Wenn die Zinsen mehrmals berechnet werden, werden zuzüglich zu den Zinsen über einen bestimmten Zeitraum Zinseszinsen für den nächsten Zeitraum berechnet. Wenn die jährliche Zinsrate und der Zins 
mal pro Jahr berechnet wird, wurden die Zinsen nach Jahren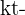 
mal berechnet und der neue Endbetrag ist
Beispiel: Es werden 
zu einem jährlichen Zinssatz von 
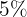angelegt. Wie hoch ist das Guthaben nach 
Jahren, wenn die Zinsen dreimal jährlich aufgezinst weden?
Um das Guthaben nach Jahren bei einer dreimaligen Aufzinsung pro Jahr zu berechnen, liegen uns folgende Werte vor: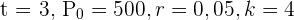 
.
Setze die Werte in die Formel ein:
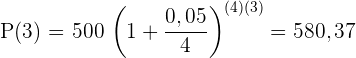
Nach Jahren liegt das Guthaben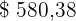 
Stetige Verzinsung
Um den Endwert einer Investition nach Jahren mit stetiger Verzinsung zu ermitteln, d.h. wenn die Zinsen nicht monatlich, täglich oder jährlich, sondern stetig berechnet werden sollen, verwenden wir folgende Formel:
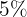Beispiel: Es werden zu einem jährlichen Zinssatz von angelegt. Wie hoch ist das Guthaben nach Jahren, wenn die Zinsen stetig verzinst werden?
Um das Guthaben nach Jahren bei einer stetigen Verzinsung zu ermitteln, verwenden wir die Werte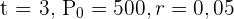 
.
Setze die Werte in die Formel ein:
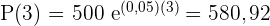
Nach Jahren liegt das Guthaben bei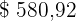 
und ist die Obergrenze für das mögliche Guthaben.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
