Kapitel

Absolutes Maximum
Eine Funktion hat ihr absolutes Maximum bei  , wenn die Ordinate größer oder gleich einem beliebigen anderen Punkt im Funktionsbereich ist.
, wenn die Ordinate größer oder gleich einem beliebigen anderen Punkt im Funktionsbereich ist.
In der folgenden Grafik hat die Funktion ihr absolutes Maximum bei 
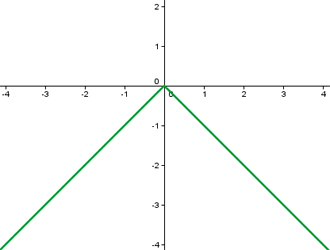
Absolutes Minimum
Eine Funktion hat ihr absolutes Minimum bei  , wenn die Ordinate kleiner oder gleich einem beliebigen anderen Punkt im Bereich der Funktion ist.
, wenn die Ordinate kleiner oder gleich einem beliebigen anderen Punkt im Bereich der Funktion ist.
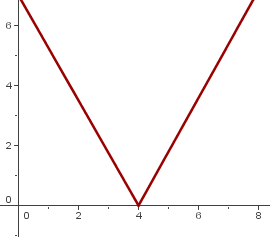
In der folgenden Grafik hat die Funktion ihr absolutes Minimum bei 
Relatives Maximum und Minimum
Eine Funktion  hat ein relatives Maximum bei
hat ein relatives Maximum bei  , wenn
, wenn 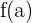 größer als oder gleich den Punkten neben
größer als oder gleich den Punkten neben  ist.
ist.
Eine Funktion  hat ein relatives Minimum bei
hat ein relatives Minimum bei  , wenn
, wenn 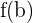 kleiner oder gleich den Punkten nahe
kleiner oder gleich den Punkten nahe  ist.
ist.
Berechnung von relativen Maxima und Minima
Die folgende Methode ist bekannt als das Kriterium der zweiten Ableitung
1 Berechne die erste und zweite Ableitung der Funktion  .
.
2 Setze die erste Ableitung gleich Null und eliminiere die Variable  . Dieses Ergebnis ist als kritische Punkte bekannt.
. Dieses Ergebnis ist als kritische Punkte bekannt.
3 Setze die kritischen Punkte in die zweite Ableitung ein:
Wenn das Ergebnis positiv ist, sagt man, dass die Funktion ein Minimum am kritischen Punkt hat.
Wenn das Ergebnis negativ ist, sagt man, dass die Funktion ein Maximum am kritischen Punkt hat.
Wenn das Ergebnis gleich Null ist, kannst Du keine Schlussfolgerung ziehen und das Kriterium der ersten Ableitung muss angewendet werden.
4 Ersetze die kritischen Punkte, an denen die Funktion ihr relatives Maximum oder Minimum erreicht, durch die ursprüngliche Funktion. Das erhaltene Ergebnis wird als kritischer Wert bezeichnet.
Beispiel für die Berechnung von Maximum und Minimum einer Funktion
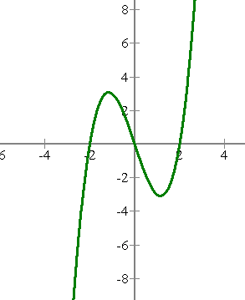
Finde die relativen Extreme von 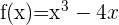
1 Berechne die erste und zweite Ableitung der Funktion  .
.
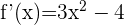

2 Suche nach den kritischen Punkten
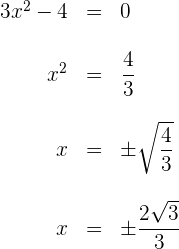
3 Setze die kritischen Punkte in die zweite Ableitung ein:
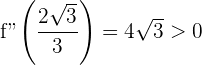
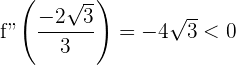
Du stellst fest, dass die Funktion ein Minimum bei  besitzt.
besitzt.
Du schließt daraus, dass die Funktion ein Maximum bei 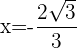 besitzt.
besitzt.
4 Berechne die kritischen Werte
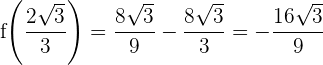
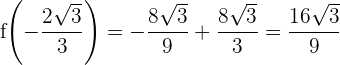
Mit KI zusammenfassen:













