Kapitel
Zusammengesetzte Funktionen
Es seien zwei Funktionen gegeben: 
und 
, bei der der Definitionsbereich letzterer Funktion in den Wertebereich ersterer eingeschlossen ist. Dadurch kann eine neue Funktion definiert werden, die mit jedem Element des Definitionsbereiches von einen Wert von 
zuordnet. Dies wird als das Zusammensetzen von Funktionen 
(gelesen wird wie folgt: 
ist abhängig von 
) bezeichnet.
Beispiele von zusammengesetzten Funktionen
Betrachte nun ein Beispiel mit den Funktionen 
und 
.
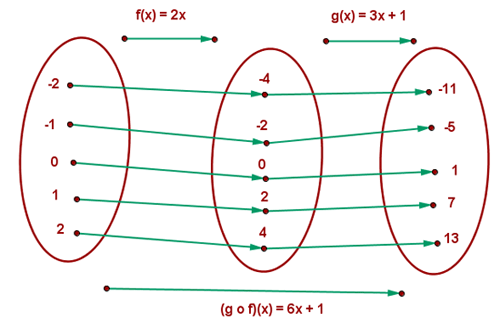
Die Zusammensetzung der Funktionen und ist: 
, also
Bei der Analyse des Definitionsbereichs der zusammengesetzten Funktion 
findest Du:
Das Zusammensetzen von Funktionen richtig beherrschen
Der Definitionsbereich von zusammengesetzten Funktionen ist wie folgt definiert:
Eigenschaften von zusammengesetzten Funktionen
1 Es gilt das Assoziativgesetz.
2 Das Kommutativgesetz gilt dagegen nicht.
3 Das neutrale Element ist die Identitätsfunktion 
.
4 Der Kehrwert der Zusammensetzung zweier Funktionen ist:
Beispiele für zusammengesetzte Funktionen
1 Es seien folgende Funktionen gegeben: 
.
1 Berechne 
.
2 Berechne 
.
2 Es seien folgende Funktionen gegeben: 
.
1 Berechne .
2 Berechne .
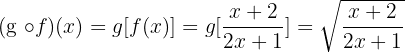
3 Es seien folgende Funktionen gegeben: 
.
1 Berechne .
2 Berechne .
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
