Wir erinnern uns, dass der Definitionsbereich einer Funktion alle Werte umfasst, die der unabhängigen Variablen zugewiesen werden können, ohne dass die Funktion unbestimmt ist. Hier werden wir den Definitionsbereich von reellen Funktionen untersuchen, d.h. von Funktionen, deren Definitionsmenge und Abbildung reelle Zahlen oder Teilmengen davon sind.
Die Definitionsmenge bei Polynomfunktionen
1 
2 
3 
Berechne die Definitionsmenge der Polynomfunktionen:
Die Definitionsmenge einer ganzwertigen Polynomfunktion ist  . Das heißt: alle reellen Zahlen.
. Das heißt: alle reellen Zahlen.
1 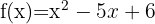

2 

3 
Beachte, dass es sich um eine Polynomfunktion mit rationalen Koeffizienten handelt: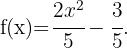 Also
Also 
Berechne die Definitionsmenge der folgenden rationalen Funktionen
1 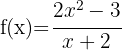
2 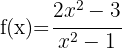
3 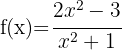
4 
5 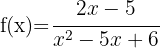
6 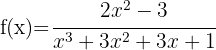
7 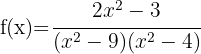
Berechne die Definitionsmenge der rationalen Funktionen:Der Definitionsbereich einer rationalen Funktion ist  minus der Werte, für die der Nenner null wird. Um die Definitionsmenge zu bestimmen, müssen wir den Nenner null setzen und die Gleichung lösen. Die Lösungen dieser Gleichung sind die Punkte, die nicht zum Definitionsbereich gehören, da sie den Nenner null setzen.
minus der Werte, für die der Nenner null wird. Um die Definitionsmenge zu bestimmen, müssen wir den Nenner null setzen und die Gleichung lösen. Die Lösungen dieser Gleichung sind die Punkte, die nicht zum Definitionsbereich gehören, da sie den Nenner null setzen.
1 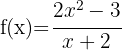

2 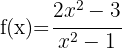

3 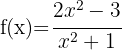
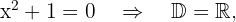
da diese Gleichung keine reellen Nullstellen hat.
4 

da die Nullstelle eine doppelte Nullstelle ist.
5 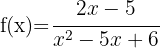
Wir haben 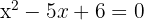 , also
, also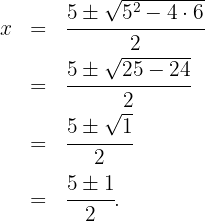
Und somit  oder
oder  . Die Definitionsmenge ist also
. Die Definitionsmenge ist also 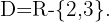
6 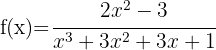
Wir stellen fest, dass das Polynom ein Binom hoch 3 ist  da
da  eine dreifache Nullstelle ist.
eine dreifache Nullstelle ist.
7 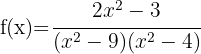
Wir faktorisieren 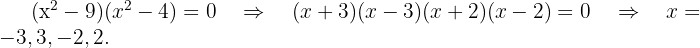
Somit 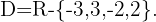
Berechne die Definitionsmenge der Wurzelfunktionen
1 
2 
3 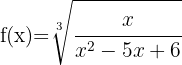
Berechne die Definitionsmenge der Wurzelfunktionen:Die Definitionsmenge einer irrationalen Funktion mit ungeradem Wurzelexponenten ist 
1 

2 
Die Definitionsmenge dieser Funktion sind alle reellen Zahlen minus der Werte, für die der Nenner der rationalen Funktion unter der Kubikwurzel null wird. Also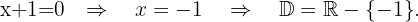
3 
Die Definitionsmenge dieser Funktion sind alle reellen Zahlen minus der Werte, für die der Nenner der rationalen Funktion unter der Kubikwurzel null wird. Also
Berechne die Definitionsmenge der Exponentialfunktionen
1 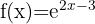
2 
Berechne die Definitionsmenge der ExponentialfunktionenDie Definitionsmenge einer Exponentialfunktion ist 
1 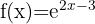

2 
Da der Exponent rational ist, gehört  nicht zur Definitionsmenge, da dadurch der Nenner null wird. Somit
nicht zur Definitionsmenge, da dadurch der Nenner null wird. Somit  .
.
Berechne die Definitionsmenge der Logarithmusfunktionen
1 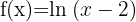
2 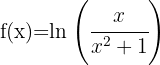
Berechne die Definitionsmenge der Logarithmusfunktionen:Damit die Funktion definiert ist, muss der Numerus positiv sein. Das heißt, die Definitionsmenge ist 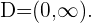
1 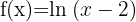
Wir lösen 
c 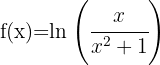
Da der Nenner immer positiv ist, befassen wir uns nur mit dem Zähler. Also
 .
.
Berechne die Definitionsmenge der Winkelfunktionen
1 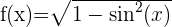
2 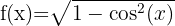
Berechne die Definitionsmenge der Winkelfunktionen: Die Definitionsmenge einer irrationalen Funktion mit geradem Wurzelexponenten besteht aus der Menge der Werte, bei denen der Radikand größer oder gleich null ist. Die Definitionsmenge der Winkelfunktionen Sinus und Kosinus sind alle reellen Zahlen. Außerdem ist der maximale Wert 1, woraus folgt, dass diese Funktionen immer Werte kleiner oder gleich 1 für jede reelle Zahl haben.
1 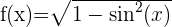
Wir lösen 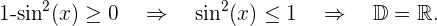
Berechne die Definitionsmenge der Winkelfunktionen:Die Definitionsmenge einer irrationalen Funktion mit geradem Wurzelexponenten besteht aus der Menge der Werte, bei denen der Radikand größer oder gleich null ist. Die Definitionsmenge der Winkelfunktionen Sinus und Kosinus sind alle reellen Zahlen. Außerdem ist der maximale Wert 1, woraus folgt, dass diese Funktionen immer Werte kleiner oder gleich 1 für jede reelle Zahl haben.
1 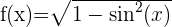
Wir lösen 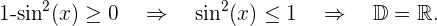
Berechne die Definitionsmenge der Winkelfunktionen:Die Definitionsmenge einer irrationalen Funktion mit geradem Wurzelexponenten besteht aus der Menge der Werte, bei denen der Radikand größer oder gleich null ist. Die Definitionsmenge der Winkelfunktionen Sinus und Kosinus sind alle reellen Zahlen. Außerdem ist der maximale Wert 1, woraus folgt, dass diese Funktionen immer Werte kleiner oder gleich 1 für jede reelle Zahl haben.
1 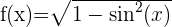
Wir lösen 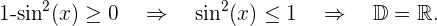
2 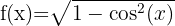
Wir lösen 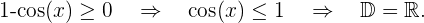
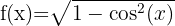
Wir lösen 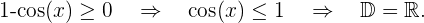
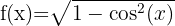
Wir lösen 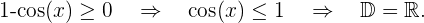
Wurzelfunktionen und ihre Definitionsmenge
1 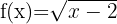
2 
3 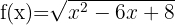
4 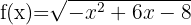
5 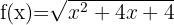
6 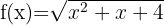
7 
8 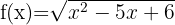
9 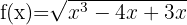
10 
11 
12 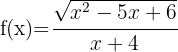
13 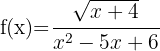
14 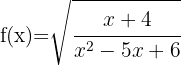
Berechne die Definitionsmenge der Wurzelfunktionen:Die Definitionsmenge einer irrationalen Funktion mit geradem Wurzelexponenten besteht aus der Menge der Werte, bei denen der Radikand größer oder gleich null ist.
1 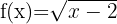
Wir lösen die Ungleichung
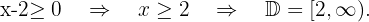
2 
Wir lösen 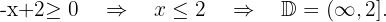
3 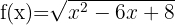
Wir lösen 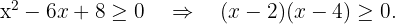 Wir setzen null, um die Nullstellen zu bestimmen:
Wir setzen null, um die Nullstellen zu bestimmen: 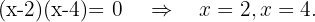
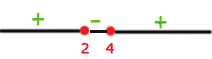
Schließlich nehmen wir die Intervalle, innerhalb derer die Ungleichheit positiv ist. Die Vereinigung dieser ist dann unsere Definitionsmenge. Deshalb ist 
4 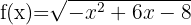
Wir lösen  Wir setzen gleich null, um die Nullstellen zu erhalten:
Wir setzen gleich null, um die Nullstellen zu erhalten: 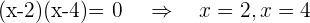
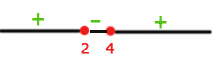
Schließlich nehmen wir die Intervalle, innerhalb derer die Ungleichheit negativ ist. Die Vereinigung dieser ist dann unsere Definitionsmenge. Deshalb ist 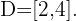
5 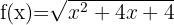
Wir lösen  da
da 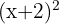 größer oder gleich null ist.
größer oder gleich null ist.
6 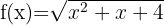
Wir lösen 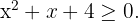 Wenn wir gleich null setzen, hat die entsprechende Gleichung keine reellen Lösungen. Außerdem stellen wir fest, dass sie bei einem beliebigen Wert positiv oder null ist. Deshalb ist
Wenn wir gleich null setzen, hat die entsprechende Gleichung keine reellen Lösungen. Außerdem stellen wir fest, dass sie bei einem beliebigen Wert positiv oder null ist. Deshalb ist 
7 
Wir lösen  Diese Ungleichheit ist nur für den Wert
Diese Ungleichheit ist nur für den Wert  erfüllt, da für alle anderen Werte von
erfüllt, da für alle anderen Werte von  das Ergebnis immer negativ ist. Somit ist
das Ergebnis immer negativ ist. Somit ist  der einzige Wert, der unsere Ungleichung erfüllt. Deshalb ist
der einzige Wert, der unsere Ungleichung erfüllt. Deshalb ist 
8 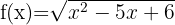
Wir lösen die Ungleichung 2. Grades 
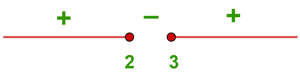
Schließlich nehmen wir die Intervalle, innerhalb derer die Ungleichheit positiv ist, und schließen die Extremwerte ein, für die sie null wird. Die Vereinigung dieser Intervalle ist dann unsere Definitionsmenge. Deshalb ist 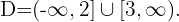
9 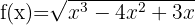
Wir lösen 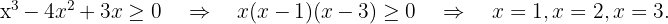
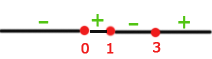
Schließlich nehmen wir die Intervalle, innerhalb derer die Ungleichheit positiv ist, und schließen die Extremwerte ein, für die sie null wird. Die Vereinigung dieser Intervalle ist dann unsere Definitionsmenge. Deshalb ist 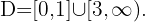
10 
Da die Wurzel im Nenner steht, muss der Radikand größer als null sein. Er darf jedoch nicht gleich null sein, da ansonsten der Nenner null wird. Wir lösen 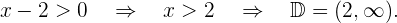
11 
In diesem Fall muss der Nenner ungleich null sein und die Wurzel des Zählers muss größer oder gleich null sein. Wir lösen 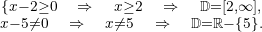 Die Lösung ist die Überschneidung der beiden Mengen. Deshalb ist
Die Lösung ist die Überschneidung der beiden Mengen. Deshalb ist 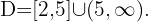
12 
Der Zähler muss größer oder gleich null sein und der Nenner muss ungleich null sein. Wir lösen 

Die Lösung ist die Überschneidung der beiden Mengen, also 
13 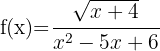
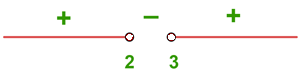
Der Nenner muss größer als null sein. Wir lösen 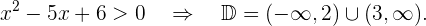
14 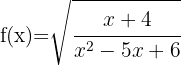
Der Radikand muss größer als null sein und der Nenner muss ungleich null sein. Wir lösen  y
y 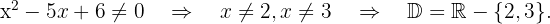

Die Lösung ist die Überschneidung der beiden Mengen, also 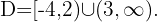
Berechne die Definitionsmenge der Funktion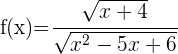
Berechne die Definitionsmenge der Funktion:
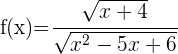
Wir lösen 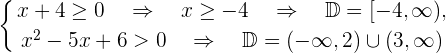 Die Lösung ist die Überschneidung der beiden Mengen, also
Die Lösung ist die Überschneidung der beiden Mengen, also 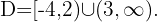
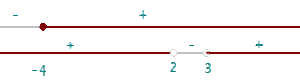
Berechne die Definitionsmenge der abschnittsweise definierten Funktion
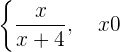
Berechne die Definitionsmenge der abschnittsweise definierten Funktion: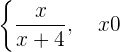
Im ersten Abschnitt muss der Nenner ungleich null sein. Im zweiten Abschnitt ist 3 eine Konstante, die immer positiv ist; wir untersuchen nur, ob der Nenner größer als null ist. Somit
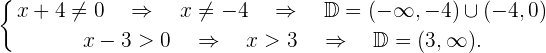
Schließlich ist die Lösung 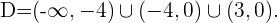
Mit KI zusammenfassen:


