Kapitel
Bei zwei Mengen 
und 
nennen wir die Zuordnung von eine Funktion, bei der alle Elemente von höchstens eine Abbildung in haben, d.h. eine Abbildung oder keine.
Eine reelle Funktion mit reeller Variable ist eine beliebige Zuordnung 
, die jedem Element einer gegebenen Teilmenge der reellen Zahlen, Definitionsmenge genannt, eine andere reelle Zahl zuordnet.
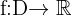
Die Teilmenge, in der die Funktion definiert ist, wird als Definitionsmenge oder Wertemenge der Funktion bezeichnet. Sie wird mit 
angegeben.
Die Zahl 
, die zur Definitionsmenge der Funktion gehört, wird als unabhängige Variable bezeichnet.
Die Zahl 
, die durch mit dem Wert verknüpft wird, wird als abhängige Variable bezeichnet. Die Abbildung von wird mit 
angegeben. Somit
Die Menge der reellen Werte, die die Variable oder annimmt, wird als Zielmenge einer Funktion bezeichnet.
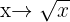
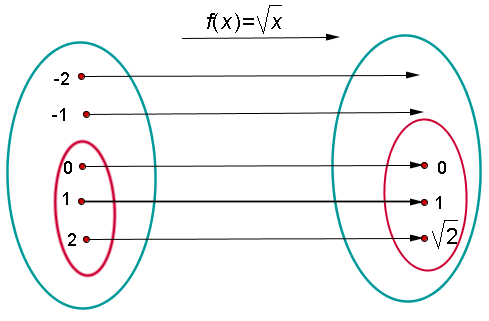
Die Definitionsmenge ist die Menge der Elemente, die eine Abbildung haben.
Die Zielmenge ist die Menge der Elemente, die Abbildungen sind.
Zusammensetzung von Funktionen
Wenn wir zwei Funktionen haben: und 
, so dass die Definitionsmenge der letzteren in der Zielmenge der ersteren enthalten ist, kann eine neue Funktion definiert werden, die jedem Element der Definitionsmenge von den Wert von 
zuordnet.
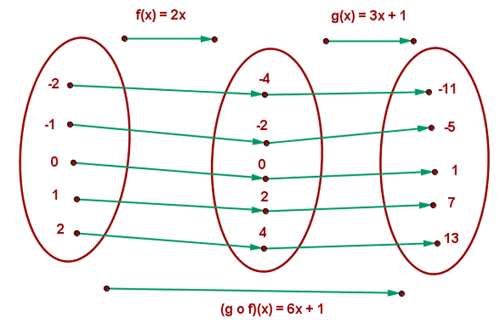
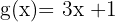
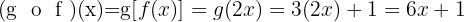
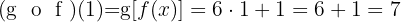
Definitionsmenge
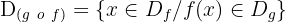
Eigenschaften
1
Assoziativ.
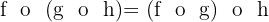
2
Nicht kommutativ.
3
Das neutrale Element ist die identische Abbildung 
.
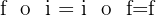
Beispiele für die Zusammensetzung von Funktionen
Gegeben sind die Funktionen:
1
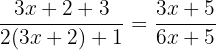
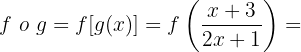
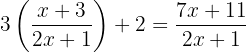
2
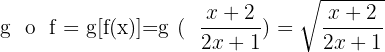
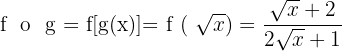
3
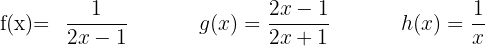
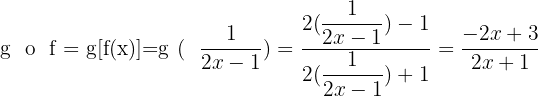
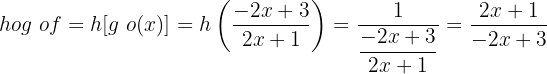
Umkehrfunktion
Die Umkehrfunktion oder inverse Funktion von ist eine andere Funktion 
, die folgende Bedingung erfüllt:
Wenn 
, ist 
.
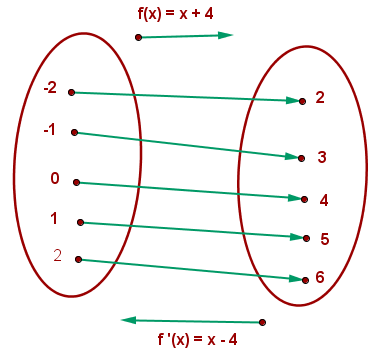
Wir stellen fest:
Die Definitionsmenge von ist die Zielmenge von .
Die Zielmenge von ist die Definitionsmenge von .
Wenn wir die Zielmenge einer Funktion ermitteln wollen, müssen wir die Definitionsmenge ihrer Umkehrfunktion bestimmen.
Wenn zwei Funktionen invers sind, ist ihre Zusammensetzung die identische Abbildung.
Die Graphen von und sind symmetrisch zur Winkelhalbierenden des 1. und 3. Quadranten.
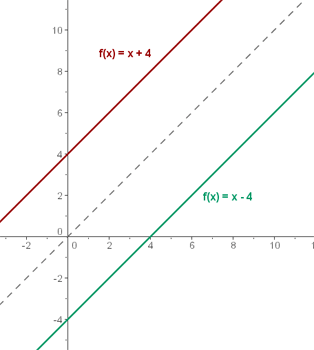
Es ist zu unterscheiden zwischen der Umkehrfunktion 
und der Umkehrfunktion einer Funktion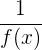 
.
Schritte für die Berechnung der Umkehrfunktion
1 Zunächst schreiben wir die Funktion in Abhängigkeit von und .
2 Wir ermitteln die Variable in Abhängigkeit der Variablen .
3 Wir vertauschen die Variablen.
Beispiele für die Berechnung der Umkehrfunktion
1
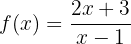
Zunächst schreiben wir die Gleichung der Funktion in Abhängigkeit von und .
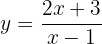
Wir führen die Berechnungen durch.
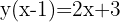
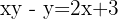
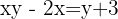
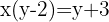
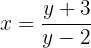
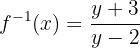
Wir überprüfen das Ergebnis für 
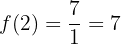
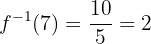
2
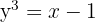
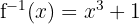
3
Es handelt sich nicht um eine Funktion.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
