Stelle die folgenden Geraden dar:
- y = 2
- y = −2
- y = x
- y = 2x − 1
- y = −2x − 1
- y = ½x − 1
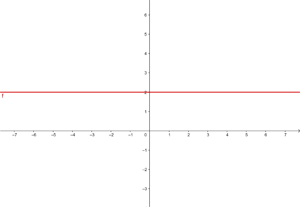
a y = 2
Es handelt sich um eine konstante Funktion
Wir ziehen eine Gerade parallel zur x-Achse durch (0, 2).
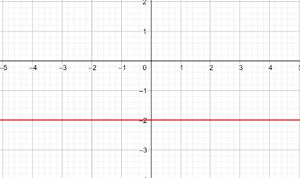
b y = −2
Es handelt sich um eine konstante Funktion
Wir ziehen eine Gerade parallel zur x-Achse durch (0, –2)
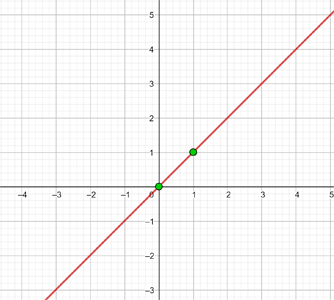
c y = x
Es handelt sich um eine identische Abbildung
| x | y=x |
|---|---|
| 0 | 0 |
| 1 | 1 |
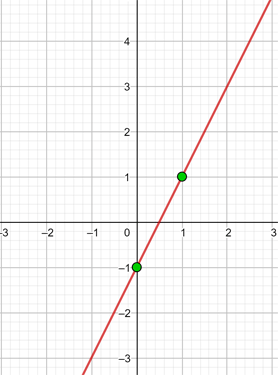
d y = 2x − 1
Es handelt sich um eine affine Funktion, die wir zu zwei Punkten generieren, um die Gerade zu bilden
| x | y = 2x −1 |
|---|---|
| 0 | -1 |
| 1 | 1 |
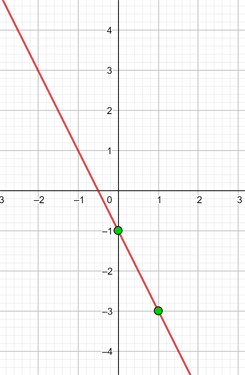
e y = −2x − 1
Es handelt sich um eine affine Funktion
| x | y = −2x −1 |
|---|---|
| 0 | -1 |
| 1 | -3 |
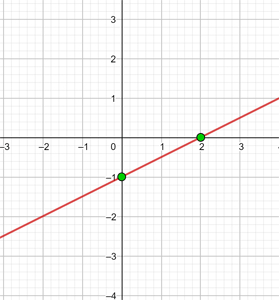
f y = ½x − 1
Es handelt sich um eine affine Funktion
| x | y = ½x − 1 |
|---|---|
| 0 | -1 |
| 2 | 0 |
Stelle die folgenden Funktionen dar
Folgendes ist bekannt:
1 Sie hat die Steigung -3 und die Ordinate im Ursprung -1.
2 Ihre Steigung beträgt 4 und sie verläuft durch den Punkt (-3, 2).
Stelle die folgenden Funktionen dar
Folgendes ist bekannt:
1 Sie hat die Steigung -3 und die Ordinate im Ursprung -1.
Es handelt sich um eine affine Funktion vom Typ y = mx + n
Die Steigung beträgt: m = –3
Die Ordinate im Ursprung ist: n = –1
die darzustellende Funktion ist:
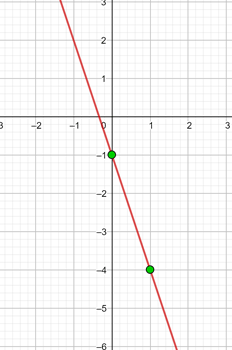
y = −3x −1
| x | y = −3x − 1 |
|---|---|
| 0 | -1 |
| 1 | -4 |
2Sie hat die Steigung 4 und verläuft durch (−3, 2).
Es handelt sich um eine affine Funktion vom Typ y = mx + n
Die Steigung ist: m = 4
Um n zu bestimmen, setzen wir den Punkt in die Funktioin ein y = 4x + n
2 = 4 · (−3) + n wir erhalten n = 14
Die Funktion ist:
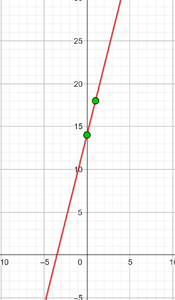
y = 4x + 14
| x | y = 4x +14 |
|---|---|
| 0 | 14 |
| 1 | 18 |
Funktionsproblem bei Sardellen
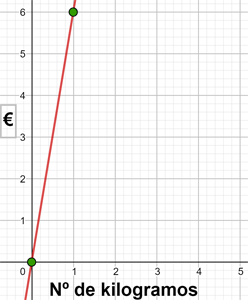
Drei Kilogramm Sardellen kosten 18 €. Schreibe und stelle die Funktion dar, die den Preis der Sardellen in Abhängigkeit von den gekauften Kilos definiert.
Drei Kilogramm Sardellen kosten 18 €. Schreibe und stelle die Funktion dar, die den Preis der Sardellen in Abhängigkeit von den gekauften Kilos definiert.
Es handelt sich um eine lineare Funktion: y = mx, wobei
-
- x die kg sind
-
- m die Kosten pro kg sind
-
- und die Gesamtkosten
Gemäß der Aufgabe haben wir y=18, x=3, also müssen wir m ermitteln
Wir setzen die Werte der unabhängigen und der abhängigen Variable ein
18 = m · 3 wir erhalten m = 6
Die Funktion ist also:
y = 6x
| x | y = 6x |
|---|---|
| 0 | 0 |
| 1 | 6 |
Problem der affinen Funktion
In den Wochen der Kultivierung einer Pflanze, die 2 cm misst, wurde beobachtet, dass ihr Wachstum direkt proportional zur Zeit ist, da sie in einer Woche von 2 cm auf 2,5 cm gewachsen ist.
Stelle eine affine Funktion auf, die die Höhe der Pflanze in Abhängigkeit von der Zeit angibt, und stelle sie grafisch dar.
In den Wochen der Kultivierung einer Pflanze, die 2 cm misst, wurde beobachtet, dass ihr Wachstum direkt proportional zur Zeit ist, da sie in einer Woche von 2 cm auf 2,5 cm gewachsen ist.
Stelle eine affine Funktion auf, die die Höhe der Pflanze in Abhängigkeit von der Zeit angibt, und stelle sie grafisch dar.
Anfangsgröße = 2 cm
Wöchentliches Wachstum = 2,5 − 2 = 0,5 cm
Wenn also x für die Anzahl der Wochen steht, dann ist 0,5x die Zunahme der Größe, die in x Wochen stattfindet, aber zu Beginn der Beobachtung beträgt sie bereits durchschnittlich 2 cm, daher lautet die Funktion:
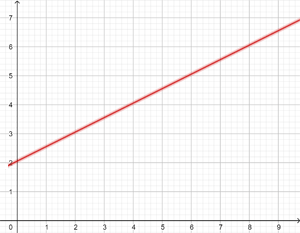
y = 0,5x + 2
Der Graph ist
Problem bei Funktionen von Temperatur und Tiefe
Wenn man in die Erde gräbt, erhöht sich die Temperatur gemäß der folgenden Formel:
t = 15 + 0,01 h.
wobei t die erreichte Temperatur in Grad Celsius und h die Tiefe in Metern ab der Erdkruste ist.
Berechne:
1 Welche Temperatur wird in einer Tiefe von 100 m erreicht?
2 Wie tief muss gegraben werden, bis eine Temperatur von 100 ºC erreicht wird?
Wenn man in der Erde gräbt, steigt die Temperatur nach der folgenden Formel:
t = 15 + 0,01 h.
Dabei ist t die erreichte Temperatur in Grad Celsius und h die Tiefe in Metern ab der Erdkruste.
Berechne:
1Welche Temperatur wird in einer Tiefe von 100 m erreicht?
Wir benötigen die abhängige Variable
t = 15 + 0,01 · 100 = 16 ºC
2Wie tief muss gegraben werden, bis eine Temperatur von 100 ºC erreicht wird?
Wir benötigen die unabhängige Variable
100 = 15 + 0,01h
0,01h = 100 – 15
0,01h=85
h =85/0,01=8500 m
Problem zur Luftverschmutzung in einer Stadt
Die Luftverschmutzung in einer Stadt beträgt um 6 Uhr morgens 30 Teile pro Million und nimmt jede Stunde linear um 25 Teile pro Million zu. Sei y die Verschmutzung zum Zeitpunkt t nach 6 Uhr morgens.
1 Bestimme die Gleichung, die y mit t in Beziehung setzt.
2 Berechne den Grad der Luftverschmutzung um 16:00 Uhr.
Die Luftverschmutzung in einer Stadt beträgt um 6 Uhr morgens 30 Teile pro Million und nimmt jede Stunde linear um 25 Teile pro Million zu. Sei y die Verschmutzung zum Zeitpunkt t nach 6 Uhr morgens.
1 Bestimme die Gleichung, die y mit t in Beziehung setzt.
y = 30 + 25t
2Berechne den Grad der Luftverschmutzung um 16:00 Uhr.
Von 6 Uhr morgens bis 16 Uhr nachmittags vergehen 10 Stunden.
f(10) = 30 + 25 · 10 = 280
Mit KI zusammenfassen:


