Willkommen auf unserer Seite, auf der wir uns den Bereich der mathematischen Graphen und Funktionen näher ansehen. Graphen und Funktionen sind das eigentliche Wesen der Mathematik und spielen eine grundlegende Rolle in einer Vielzahl von Disziplinen, von der Physik bis zu den Wirtschaftswissenschaften, von der Informatik bis zum Ingenieurwesen.
Bei dieser Gelegenheit stellen wir dir eine Reihe praktischer Übungen vor, mit denen du lernst, wie man Daten und mathematische Zusammenhänge visuell darstellt, wie man alltägliche Probleme mit linearen Funktionen löst und vieles mehr.
Bei dieser Gelegenheit stellen wir dir eine Reihe praktischer Übungen vor, mit denen du lernst, wie man Daten und mathematische Zusammenhänge visuell darstellt, wie man alltägliche Probleme mit linearen Funktionen löst und vieles mehr.
1 Stelle folgende Geraden dar:
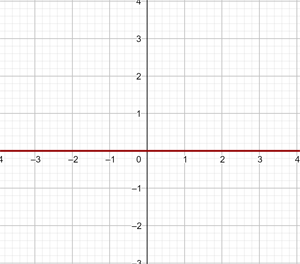
a 
Diese Funktion ist konstant
b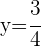 
Diese Funktion ist konstant
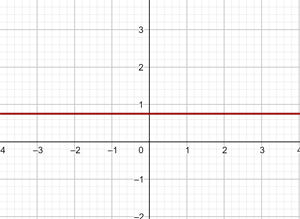
c 
Diese Funktion ist linear
 | |
|---|---|
| 0 | 0 |
| 1 | 2 |
d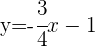 
Diese Funktion ist affin
| |
|---|---|
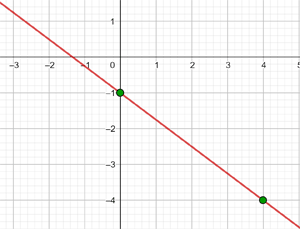
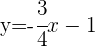| 0 | -1 |
| 4 | -4 |
Ein Wasserhahn tropft und verliert pro Minute 
cm³ Wasser. Erstelle eine Wertetabelle der Funktion, die das Verhältnis "Zeit-Wassermenge" darstellt. Stelle die Funktion dar und ermittle die dazugehörige Gleichung.
Die Funktion, die das Verhältnis "Zeit-Wassermenge" darstellt, lautet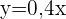
| Zeit | Wassermenge |
|---|---|
| 0 | 0 |
| 1 | 4 |
| 2 | 8 |
| 3 | 12 |
| 4 | 16 |
| ... | ... |
Folgende Abbildung zeigt den Graphen der Funktion.
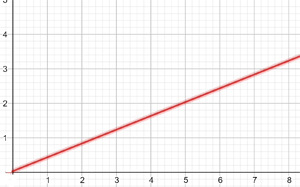
Für einen Mietwagen werden 
€ pro Tag plus 
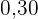€ pro Kilometer berechnet. Bestimme die Gleichung der Geraden, die die täglichen Kosten mit der Anzahl der Kilometer verbindet, und stelle sie grafisch dar. Wenn an einem Tag insgesamt 
km gefahren werden, wie hoch sind dann die Kosten?
Der zu zahlende Betrag wird durch die folgende Funktion bestimmt.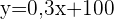
Wenn für die Anzahl der Kilometer steht, ergibt sich durch Einsetzen in die obige Gleichung der genaue Betrag, der bezahlt werden muss, nämlich
= 
€
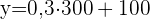Der Graph sieht schließlich wie folgt aus
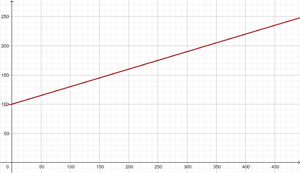
Die folgende Funktion stellt die Distanz (in Kilometern) dar, die ein Motorrad mit einer Geschwindigkeit von km/h in Abhängigkeit der Zeit t (in Stunden) zurücklegt: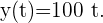
Welche Distanz legt das Motorrad in 
Stunden zurück? Und in 
Stunden?
Der Graph, der die Funktion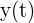 
darstellt, ist eine Gerade, die durch den Ursprung verläuft und die Steigung hat. Um die Werte bestimmen zu können, müssen wir die Abbildung von und berechnen: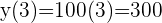 
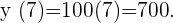. Deshalb werden in Stunden Kilometer und in Stunden 
Kilometer zurückgelegt.
Sieh dir folgende Gleichung einer Geraden an
Ermittle die Gleichung einer parallelen Geraden, die durch den Punkt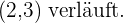 
Die Steigung einer Geraden ist der Koeffizient, der die Variable begleitet. Um eine parallele Gerade zu erhalten, muss diese dieselbe Steiung haben wie die Ausgangsgerade. Der Graph der Funktion ist eine Gerade, die durch den Punkt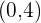 
verläuft und die Steigung 
hat. Auf diese Weise haben alle Geraden, die parallel zur Ausgangsgeraden verlaufen, die Gleichung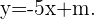 
Wir müssen also nur den Wert für 
bestimmen. Hiefür setzen wir die Werte für und 
des angegebenen Punkts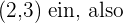 
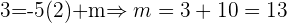. Die Gleichung der gesuchten Geraden ist somit gegeben durch 
Die Stadtwerke Augsburg berechnen für Wasser folgende Gebühren: eine Gebühr von 
€ pro Monat sowie 
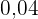€ pro Kubikmeter. Berechne die Funktion, die die Kosten der monatlichen Rechnung der Stadtwerke Augsburg in Abhängigkeit von den verbrauchten Kubikmetern angibt.
Wenn Augsburg ingesamt Kubikmeter Wasser verbraucht, liegen die Gesamtkosten bei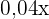 
. Außerdem muss noch die Gebühr von € addiert werden. Die Funktion lautet also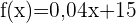 
. Der Graph der Funktion ist eine Gerade, die durch den Punkt 
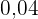verläuft und die Steigung hat.
Die folgende Funktion stellt die Anzahl der pro Tag verkauften T-Shirts in einem Bekleidungsgeschäft dar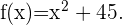
Wieviele T-Shirts werden in Tagen verkauft? Und in 
Tagen? Und in 
Tagen?
Der Graph der Funktion ist durch den Graphen einer auf der Ordinatenachse zentrierten Parabel mit dem Wendepunkt bei 
gegeben. Die folgende Tabelle zeigt die Werte, die wir für die Funktion benötigen und die die Anzahl der T-Shirts angeben.
| (Anzahl der Tage) |  |
|---|---|
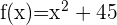| 3 | 54 |
| 5 | 70 |
| 35 | 1270 |
Sara plant eine Tour von Stadt A nach Stadt B. Sie möchte die Strecke, die sie jeden Tag zurücklegt, verfolgen und ein Diagramm erstellen, um ihren Fortschritt zu veranschaulichen. Sara hat eine Karte, auf der die Entfernungen zwischen verschiedenen Städten entlang des Weges eingezeichnet sind. Die Entfernungen zwischen den Städten sind wie folgt:
Sara plant, am ersten Tag von Stadt A nach Stadt X, am zweiten Tag von Stadt X nach Stadt Y, am dritten Tag von Stadt Y nach Stadt Z und am vierten Tag von Stadt Z nach Stadt B zu fahren.
- Erstelle ein Diagramm, das Saras Reise darstellt, wobei die zurückgelegte Strecke auf der vertikalen Achse und die Tage der Reise auf der horizontalen Achse liegen. Beschrifte die Tage als Tag 1, Tag 2, Tag 3 und Tag 4. Markiere die Entfernungen, die an jedem Tag zurückgelegt werden, indem du die Entfernungen zwischen den Städten angibst.
- Welche lineare Gleichung verläuft durch diese Punkte?
- Die erste Koordinate unserer Punkte entspricht dem Tag und die zweite Koordinate entspricht der an diesem Tag zurückgelegten Strecke. Der Graph ist als
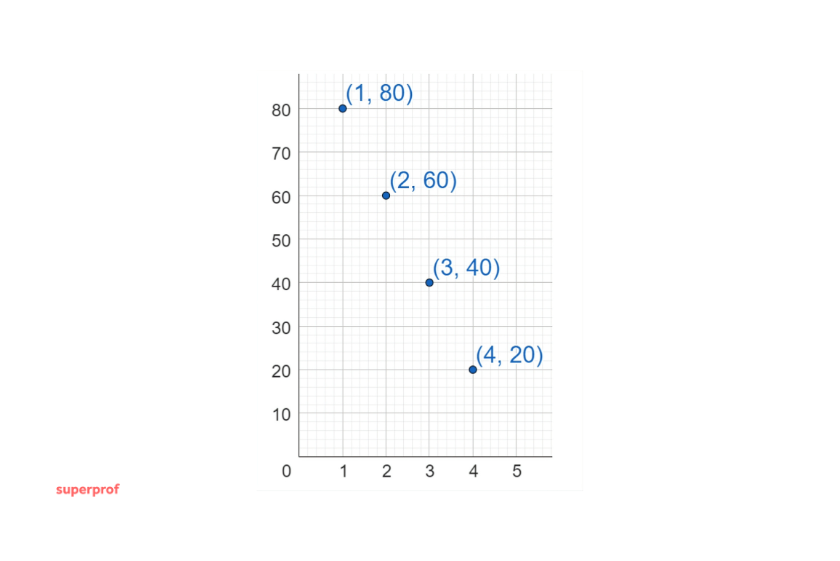
- Beachte: Wenn wir zwei Punkte
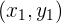und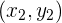 
haben, ist die Gerade, die durch diese Punkte verläuft, gegeben durch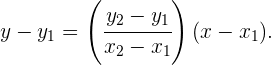
In diesem Fall nehmen wir die Punkte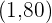
und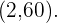 
Somit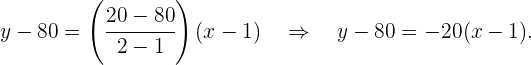
Die Gleichung der gesuchten Geraden lautet also
Der Gewinn eines Unternehmens hat seinen Umsatz in Tausend Euro mit der Gleichung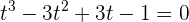 
im Intervall 
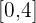gebildet, wobei jedes Einheitsintervall ein Viertel eines Jahres darstellt.
- Bei welchen Werten von
wird ein Umsatz von 0 Euro registriert? - Neigt das Unternehmen nach dem ersten Quartal des Jahres dazu, seinen Umsatz zu steigern oder zu senken?
- Die Gleichung ist äquivalent zu
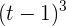, sodass das Unternehmen nur bei 
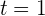einen Umsatz von 0 Euro verbucht. - Es kann seinen Umsatz steigern, da für alle
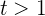erfüllt ist, dass 
Ein bekannter Autor behauptet, er habe ein ganzes Buch in 
Stunden geschrieben. In der ersten Stunde schrieb er 
Wörter pro Minute und in der zweiten Stunde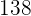 
pro Minute, ganz ohne Unterbrechung.
- Wie viele Wörter hat er in der ersten Stunde geschrieben?
- Und in der zweiten Stunde?
- Die erste Stunde kann mittels der Gleichung
dargestellt werden, wobei 
für die Minuten steht. Somit wurden innerhalb von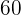 
Minuten 
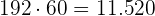Wörter geschrieben. - Zu Beginn der zweiten Stunde verringert der Autor seine Schreibgeschwindigkeit. Dies zeigt die Gleichung
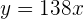, wobei wieder für die Minuten steht. Er hat in der zweiten Stunde also nur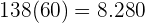 
Wörter geschrieben. Insgesamt hat er somit 
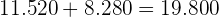Wörter geschrieben.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
