Kapitel
Manchmal stellt man fest, dass eine Funktion eine Unbestimmtheit von unendlich geteilt durch unendlich hat. Das heißt, betrachte die Funktion
so dass 
y 
. Daher wäre die Funktion, ausgewertet nach 
also
In diesem Fall ist die Funktion bei unbestimmt, da es nicht möglich ist, 
einen beliebigen Wert zuzuordnen. Du kannst jedoch eine der beiden folgenden Methoden anwenden, um den Grenzwert der Funktion bei —zu finden - beachte, dass der Grenzwert bei nicht mit dem Wert von — identisch ist:
Erste Methode: Vergleich der Ordnung der Polynome
Diese Methoden funktionieren nur bei rationalen Funktionen der Form
wobei 
und 
Polynome und einige sehr spezielle Fälle wie Exponentiale und Radikale sind. In Ermangelung solcher Fälle gibt es andere Methoden wie die L'Hôpital-Regel.
Die erste Methode besteht im Vergleich der Grade von und :
Der Zähler hat einen höheren Grad als der Nenner
Wenn der Zähler einen höheren Grad hat als der Nenner, dann ist der Grenzwert 
oder 
. Das Vorzeichen des Grenzwerts ist das gleiche wie das Vorzeichen der Division der Koeffizienten höheren Grades. Im zweiten Beispiel unten ist zu beachten, dass der Grenzwert ist, weil die Division der Koeffizienten 
; ist, d. h. ein negatives Vorzeichen hat.
Der Grad des Nenners ist größer als der Grad des Zählers
Wenn der Grad des Nenners größer ist als der Grad des Zählers, dann ist der Grenzwert immer 0.
Zähler und Nenner haben den gleichen Grad
Wenn der Zähler und der Nenner den gleichen Grad haben, ist der Grenzwert der Quotient der Koeffizienten höheren Grades. Schaue Dir das folgende Beispiel an. Der Zähler hat den Hauptkoeffizienten 2, während der Nenner den Hauptkoeffizienten 3 hat. Da beide Polynome den gleichen Grad haben, ist der Grenzwert also 
.
Sonderfälle der Vergleichsmethode
Gegeben ist die Funktion
es gibt Fälle, in denen Du 
y 
auf ähnliche Weise vergleichen kannst, wie Du Polynome vergleichst. In diesen Fällen geht es um Exponentialfunktionen und Wurzelfunktionen.
1 Wenn oder Exponentiale sind, dann kann man sich vorstellen, dass ihr Grad immer größer ist als der eines beliebigen Polynoms (formal gesehen ist ein Exponential von höherer Ordnung als ein Polynom). Wenn sowohl Zähler als auch Nenner exponentiell sind, hat das Exponential mit der größeren Basis die höhere Ordnung.
2 Ist der Zähler oder Nenner ein Radikal der Form
,
dann betrachtest Du ihren Grad als 
und ihren höchsten Gradkoeffizienten als 
.
Zweite Methode: Zähler und Nenner werden durch dieselbe Funktion geteilt
Da
dann kannst Du eine Funktion mit multiplizieren und dividieren, um den Grenzwert einfacher zu berechnen. Der Grund dafür ist
Quotient von Polynomen
Handelt es sich um einen Quotienten von Polynomen, so werden beide Polynome durch die Potenz des höheren Grades geteilt. Zum Beispiel, wenn Du hast
Teile jedes Polynom durch 
, vereinfache die Brüche und wende den Grenzwert an:
Es ist wichtig, das Vorzeichen der Koeffizienten höchsten Grades von Zähler und Nenner zu beachten, da dies das Vorzeichen der Unendlichkeit ändern kann. Wie bei der vorherigen Methode ist das Vorzeichen das gleiche wie der Quotient der Koeffizienten höheren Grades.
Exponentialfunktion
Handelt es sich um Exponentialfunktionen, so wird durch die höhere Basis der Exponentialfunktion geteilt. Betrachte das folgende Beispiel:
Zunächst wendest Du die Eigenschaften des Produkts und des Quotienten von Potenzen an, um die Additionen oder Subtraktionen der Exponenten zu entfernen:
Dividiere Zähler und Nenner durch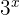 
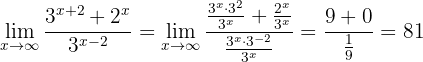
Beispiele für die unbestimmte Unendlichkeit geteilt durch Unendlichkeit
Löse nun einige Beispiele, um das eben Gesehene in die Praxis umzusetzen.
1 
Das Ergebnis ist 
, da der Zähler eine höhere Ordnung hat als der Nenner.
2 
Jetzt hast Du einen Nenner, der eine höhere Ordnung hat als der Zähler. Daher ist der Grenzwert 0.
3 
In diesem Fall hast Du eine Wurzelfunktion im Zähler. Daher nimmst Du an, dass der Grad 
ist. Da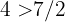 
, ist der Grenzwert also 0.
4 
Wie bereits erwähnt, haben Exponentialfunktionen immer eine höhere Ordnung als Polynome - auch wenn diese vom Grad 23 ist. Der Grenzwert ist also .
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
