Kapitel
Kontinuität einer Funktion an einem Punkt
Eine Funktion 
ist stetig am Punkt 
, wenn ausschließlich die 3 folgenden Bedingungen erfüllt sind:
- Die Funktion ist am Punkt
definiert, d. h. für den Punkt 
existiert die Abbildung 
.
- Der Grenzwert
der Funktion existiert, wenn 
gegen den Punkt konvergiert. Die seitlichen Grenzwerte sind also gleich: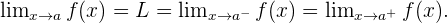
- Der Grenzwert von ist gleich dem Wert , wenn gegen den Punkt konvergiert. Mathematisch ausgedrückt bedeutet das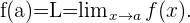
Links- und rechtsseitige Stetigkeit
Die seitliche Stetigkeit an einem Punkt ist ähnlich definiert wie die Stetigkeit an einem Punkt, mit dem Unterschied, dass hier nur einer der seitlichen Grenzwerte existieren muss. Man kann also die seitliche Stetigkeit in zwei Fälle unterteilen: links- und rechtsseitige Stetigkeit.
Linksseitige Stetigkeit
Eine Funktion ist linksseitig stetig am Punkt , wenn die drei folgenden Bedingungen erfüllt sind:
- Die Funktion ist am Punkt definiert. Das heißt, für den Punkt existiert die Abbildung .
- Der linksseitige Grenzwert von existiert, wenn auf der linken Seite gegen den Punkt konvergiert. Das heißt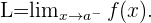
- Der Grenzwert der Funktion ist gleich dem Wert , wenn auf der linken Seite gegen den Punkt konvergiert. Das heißt:
Rechtsseitige Stetigkeit
Eine Funktion ist am Punkt rechtsseitig stetig, wenn die folgenden drei Bedingungen erfüllt sind:
- Die Funktion ist am Punkt definiert. Das heißt, für den Punkt existiert die Abbildung .
- Der linksseitige Grenzwert der Funktion existiert, wenn auf der rechten Seite gegen den Punkt konvergiert.
- Der Grenzwert von ist gleich dem Wert , wenn auf der rechten Seite gegen den Punkt konvergiert. Das heißt: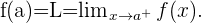
Stetigkeit von Funktionen
Es gibt verschiedene Arten von stetigen Funktionen, z. B. stetige Funktionen in allen Punkten ihres Definitionsbereichs oder stetige Funktionen in nur einigen Teilen ihres Definitionsbereichs. Beispiele für stetige Funktionen an allen Punkten ihres Definitionsbereichs sind Polynomfunktionen, rationale Funktionen, Wurzelfunktionen, Exponentialfunktionen, Logarithmusfunktionen sowie trigonometrische Funktionen.
Die folgenden Fälle sind besondere Beispiele: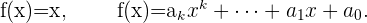
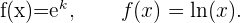
Abschnittsweise definierte Funktionen
Abschnittsweise definierte Funktionen sind der Hauptfall von Funktionen, die nur in einigen Teilen oder Intervallen ihres Definitionsbereichs stetig sind. Ein Beispiel für eine abschnittsweise definierte Funktion lautet wie folgt
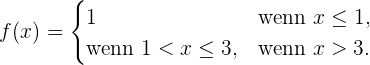
Wir können diese Art von Funktionen als Funktionen untersuchen, die ihrerseits durch andere Funktionen definiert sind. Im obigen Beispiel würde dies bedeuten, dass 
durch die konstanten Funktionen 
auf dem Intervall oder Abschnitt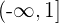 
, die Identität in 
und die konstante Funktion 
in 
definiert ist.
In diesem Zusammenhang ist eine abschnittsweise definierte Funktion stetig, wenn jede Funktion auf ihrem Definitionsintervall stetig ist. Außerdem ist sie in den Punkten der Division der Intervalle stetig.Dies bedeutet, dass ihre seitlichen Grenzwerte übereinstimmen müssen.
Das heißt, wenn wir die Stetigkeit von zeigen möchten, müssten wir die Stetigkeit der konstanten Funktion innerhalb des Intervalls 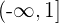(inklusive der Stetigkeit im Extremwert 1), die identische Abbildung innerhalb von (inklusive der Stetigkeit im Extremwert 3) und die konstante Funktion in überprüfen.
Rechenoperationen mit stetigen Funktionen
Es ist wichtig zu beachten, dass wir anhand gegebener stetiger Funktionen andere stetige Funktionen erzeugen können. Wir können dies durch die Grundrechenarten Addition, Subtraktion, Multiplikation, Division und Komposition erreichen.
Die Bedingungen für die Überprüfung der Stetigkeit in diesen Kombinationen sind wie folgt
Wenn und 
in stetig sind, gilt:
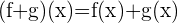ist stetig in .
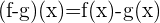ist stetig in .
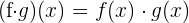ist stetig in .
- Wenn
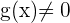, ist 
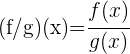
stetig in. 
ist stetig in .
Zum Beispiel sind die Funktionen 
und 
in allen Punkten ihres Definitionsbereichs stetig. Somit sind die Funktionen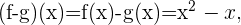
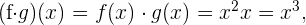
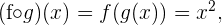
stetig. Und wenn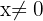 
, folgt daraus, dass 
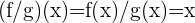ebenfalls stetig ist.
Arten der Unstetigkeit
Es gibt Funktionen, die Punkte haben, in denen sie nicht der Definition der Stetigkeit entsprechen. Diese Punkte werden als Unstetigkeitsstellen bezeichnet. Es ist wichtig zu betonen, dass es mehrere Arten von Unstetigkeit gibt, auf die wir im Folgenden eingehen werden.
Hebbare Unstetigkeitsstelle
Die hebbare Unstetigkeitsstelle einer Funktion in einem Punkt zeigt sich, wenn der folgende Grenzwert existiert: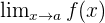
.
Wir unterscheiden zwei Arten.
Arten
1. Die Funktion ist für nicht definert.
Das bedeutet, dass der Wert nicht existiert.
Wir können diese Unstetigkeitsstelle entfernen, indem wir für einen Wert definieren. Dieser Wert muss gleich dem Grenzwert von sein, wenn gegen konvergiert. Das heißt,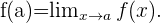
2. Die Abbildung stimmt nicht mit dem Grenzwert überein.
In diesem Fall exstiert sowohl der Wert 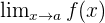als auch der Wert , jedoch stimmen diese Werte nicht überein.
Diese Unstetigkeit lässt sich entfernen, indem man den Wert von so umdefiniert, dass der neue Wert gleich dem Grenzwert von ist, wenn gegen konvergiert. Das heißt,
Nicht hebbare Unstetigkeitsstelle
Eine Unstetigkeitsstelle ist nicht hebbar oder erster Art, wenn die seitlichen Grenzwerte in existieren, jedoch unterschiedlich sind. Gleichbedeutend,
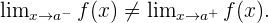
In dieser Klasse der Unstetigkeit gibt es ebenfalls zwei Arten
Arten
1. Sprungstelle: endlich
Das bedeutet, dass die Differenz zwischen den seitlichen Grenzwerten eine reelle Zahl ist. Mathematisch ausgedrückt:
2. Sprungstelle: unendlich
In diesem Fall ist die Differenz zwischen den seitlichen Grenzwerten unendlich. Das heißt, 
Wesentliche Unstetigkeit
Schließlich gibt es noch eine weitere Art der Unstetgigkeit, bei der der Grenzwert 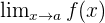nicht existiert.
Man sagt, dass eine Unstetigkeitsstelle wesentlich oder zweiter Art ist, wenn mindestens einer der seitlichen Grenzwerte in nicht existiert.
Stetigkeit auf einem Intervall
Stetigkeit auf einem abgeschlossenen Intervall
Einer der wichtigsten Fälle der Stetigkeit von Funktionen ist die Stetigkeit der Funktion auf einem abgeschlossenen Intervall. Das liegt daran, dass die Funktion neben der Stetigkeit noch andere Eigenschaften hat – sie ist zum Beispiel beschränkt.
Man sagt, dass eine Funktion auf dem abgeschlossenen Intervall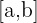 
stetig ist, wenn:
- ist stetig in für alle , die zum offenen Intervall
gehören.
- ist rechtsseitig stetig in . Das heißt:
- ist linksseitig stetig in
. Das heißt: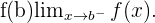
Als Beispiel sehen wir uns folgende Funktion an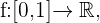 
, sodass 
.
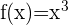Diese Funktion ist stetig auf dem Intervall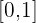 
und auf diesem Intervall außerdem beschränkt. Sie erreicht ihren Minimalwert gleich 
in 
und somit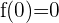 
; ihren Maximalwert gleich in 
und somit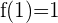 
.
Schlussfolgerung
Wenn also auf dem geschlossenen Intervall 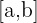stetig ist, ist auf diesem Intervall beschränkt. Dies bedeutet, dass die Funktion ihr Maximum und Minimum innerhalb des Intervalls 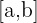erreicht, wie im obigen Beispiel.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
