Stelle graphisch dar und bestimmte die Koordinaten der Brennpunkte, der Scheitelpunkte und die Exzentrizität der folgenden Hyperbeln.
1
2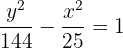
3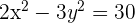
4
1
Aus der Gleichung der Hyperbel ergibt sich
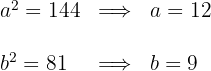
Wir erhalten den Wert für 
Da uns 
bekannt sind, die Hyperbel ihren Mittelpunkt im Ursprungspunkt hat und ihre Hauptachse horizontal ist, können wir die Scheitelpunkte 
, die Brennpunkte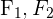 
und die Exzentrizität 
bestimmen
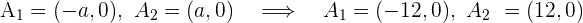
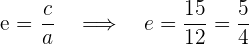
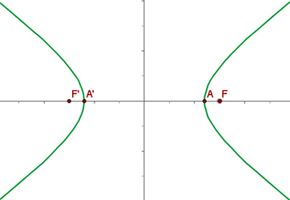
Mit den vorhergehenden Werten können wir die Hyperbel graphisch darstellen
2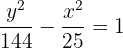
Aus der Gleichung der Hyperbel ergibt sich
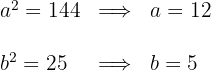
Wir erhalten den Wert für
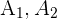Da uns bekannt sind, die Hyperbel ihren Mittelpunkt im Ursprungspunkt hat und ihre Hauptachse vertikal ist, können wir die Scheitelpunkte , die Brennpunkte 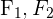und die Exzentrizität bestimmen
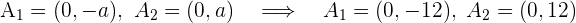
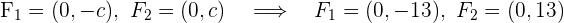
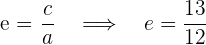
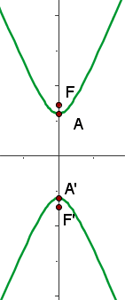
Mit den vorhergehenden Werten können wir die Hyperbel graphisch darstellen
3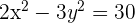
Wir dividieren durch 30
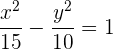
Aus der Gleichung der Hyperbel ergibt sich
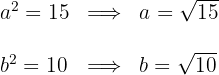
Wir erhalten den Wert für
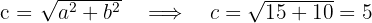
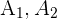Da uns bekannt sind, die Hyperbel Ihren Mittelpunkt im Ursprungspunkt hat und ihre Hauptachse horizontal ist, können wir die Scheitelpunkte , die Brennpunkte 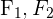und die Exzentrizität bestimmen
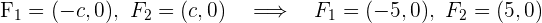
Mit den vorhergehenden Werten können wir die Hyperbel graphisch darstellen
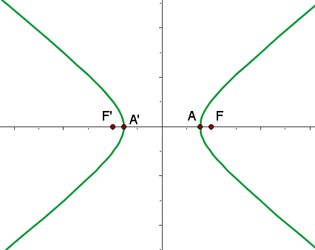
4
Wir dividieren durch 1296
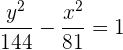
Aus der Gleichung der Hyperbel ergibt sich
Wir erhalten den Wert für
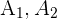Da uns bekannt sind, die Hyperbel ihren Mittelpunkt im Ursprungspunkt hat und ihre Hauptachse vertikal ist, können wir die Scheitelpunkte , die Brennpunkte 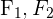und die Exzentrizität bestimmen
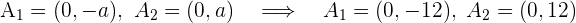
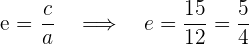
Mit den vorhergehenden Werten können wir die Hyperbel graphisch darstellen
Stelle graphisch dar und bestimme die Koordinaten des Mittelpunkts, der Brennpunkte, der Scheitelpunkte und die Exzentrizität der folgenden Hyperbeln:
1
2
1 Wir haben die gewöhnliche Gleichung der Hyperbel
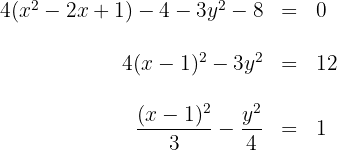
Aus der Gleichung der Hyperbel ergibt sich der Mittelpunkt und
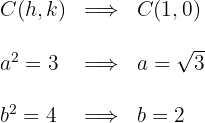
Wir erhalten den Wert für
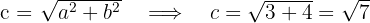
Da uns bekannt sind, wir ihren Mittelpunkt kennen und wissen, dass ihre Hauptachse horizontal ist, können wir die Scheitelpunkte 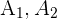, die Brennpunkte 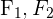und die Exzentrizität bestimmen
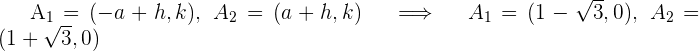
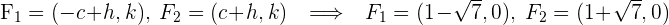
Mit den vorhergehenden Wert können wir die Hyperbel graphisch darstellen
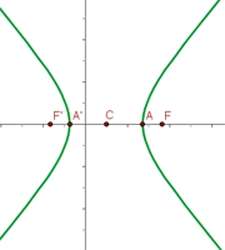
2
Wir haben die gewöhnliche Gleichung der Hyperbel
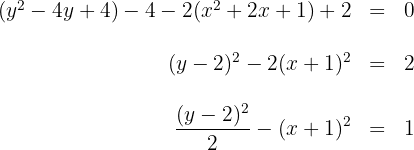
Aus der Gleichung der Hyperbel ergibt sich der Mittelpunkt und
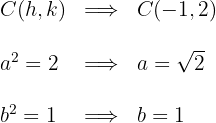
Wir erhalten den Wert für
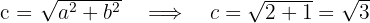
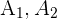Da uns bekannt sind, wir ihren Mittelpunkt kennen und wissen, dass ihre Achse horizontal ist, können wir die Scheitelpunkte , die Brennpunkte 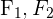und die Exzentrizität bestimmen
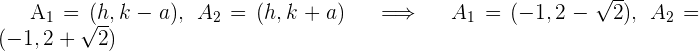
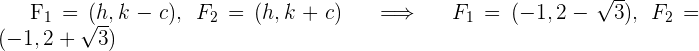
Mit den vorhergehenden Werten können wir die Hyperbel graphisch darstellen
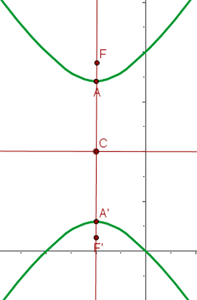
Bestimme die Gleichung einer Hyperbel, deren Mittelpunkt im Ursprungspunkt liegt. Die horizontale Hauptachse entspricht 
und die Brennstrecke entspricht 
.
Da wir die Hauptachse und die Brennstrecke kennen, ergibt sich
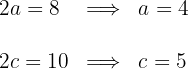
Wir erhalten den Wert für 
Die Gleichung der Hyperbel ist
Die Hauptachse einer Hyperbel ist horizontal und misst 
. Bestimme ihre Gleichung, wenn sich der Mittelpunkt im Ursprungspunkt befindet und die Kurve durch den Punkt 
verläuft.
Die Gleichung der Hyperbel hat die Form
Um 
zu erhalten, nutzen wir die Hauptachse
Um 
zu bestimmen, setzen wir und den Punkt in die Gleichung der Hyperbel ein
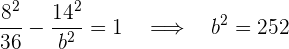
Die gesuchte Gleichung ist
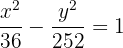
Berechne die Gleichung der Hyperbel in 1. Hauptlage, deren Brennstrecke 
entspricht; die Strecke von einem Brennpunkt zum nächstgelegenen Scheitelpunkt beträgt 
und der Mittelpunkt befindet sich im Ursprungspunkt.
Die Gleichung der Hyperbel hat die Form
Da wir die Brennstrecke und den Abstand zwischen Brennpunkt und Scheitelpunkt kennen, ergibt sich
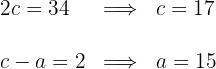
Wir erhalten den Wert für
Die Gleichung der Hyperbel ist
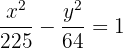
Bestimme die Gleichung der horizontalen Hyperbel in 1. Hauptlage mit dem Mittelpunkt im Ursprungspunkt, die durch die Punkte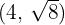 
und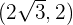 
verläuft
Die Gleichung der Hyperbel hat die Form
Um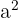 
und zu bestimmen, ersetzen wir die gegebenen Punkte in der Gleichung der Hyperbel
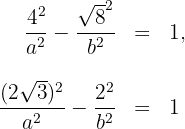
Durch das Lösen des Gleichungssystems erhalten wir
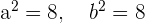
Die gesuchte Gleichung ist
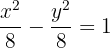
Bestimme die Gleichung der Hyperbel in 1. Hauptlage mit dem Mittelpunkt im Ursprungspunkt, die durch den Punkt 
verläuft und deren Exzentrizitä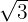t 
ist
Die Gleichung der Hyperbel hat die Form
wir setzen den gegebenen Punkt in die Gleichung der Hyperbel ein und erhalten folgende Gleichung
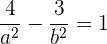
Aus der Exzentrizität ergibt sich folgende Gleichung
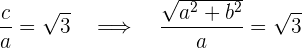
Indem wir das System, das sich aus den beiden vorherigen Gleichungen ergibt, lösen, erhalten wir 
und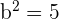 
Die gesuchte Gleichung ist
Bestimme die Gleichung der horizontalen Hyperbel in 1. Hauptlage mit dem Mittelpunkt im Ursprungspunkt; ein Brennpunkt liegt 
und von den Scheitelpunkten entfernt
Aus den erhaltenen Werten ergibt sich die Hauptachse und die Brennstrecke
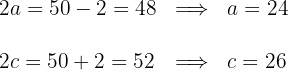
Wir erhalten den Wert für
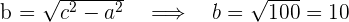
Die Gleichung der Hyperbel ist
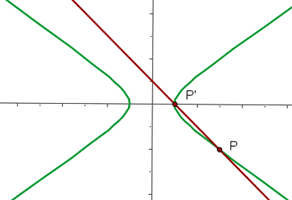
Bestimme die relative Lage der Geraden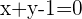 
im Hinblick auf die Hyperbel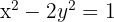 
Wir lösen das Gleichungssystem, das durch die Gerade und die Hyperbel gebildet wird
Wir erhalten die Schnittpunkte 
und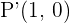 
Somit schneidet die Gerade die Hyperbel
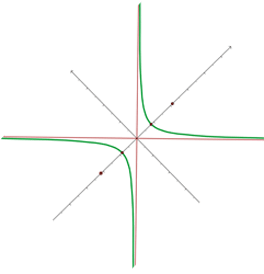
Eine gleichseitige Hyperbel verläuft durch den Punkt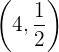 
. Die Gleichung bezieht sich auf die Asymptoten als Achsen und die Koordinaten der Scheitelpunkte und der Brennpunkte.
Die Gleichung der gleichseitigen Hyperbel ist
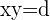
Wir ersetzen den Punkt, durch den die Hyperbel verläuft
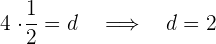
Die Gleichung, die sich auf ihre Asymptoten als Achsen bezieht, lautet also
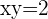
Um die Scheitelpunkt zu erhalten, schneiden wir die Gerade, die die Scheitelpunkte enthält, mit der Hyperbel
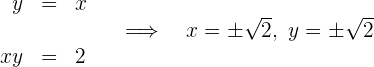
Die Scheitelpunkte si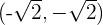nd 
und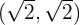 
Wir wissen, dass 
und die dazugehörige Gleichung 
lautet. Um die Brennpunkte zu bestimmen, schneiden wir die vorherige Gleichung mit der Geraden, die die Scheitelpunkte enthält.
Die Brennpunkte sind 
und 
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
