Kapitel
- Gleichung der Hyperbel in 1. Hauptlage mit Nullpunkt als Mittelpunkt und horizontaler Hauptachse
- Gleichung der Hyperbel in 1. Hauptlage mit Nullpunkt als Mittelpunkt und vertikaler Hauptachse
- Gleichung der Hyperbel in 1. Hauptlage, deren Mittelpunkt nicht der Nullpunkt ist, mit horizontaler Hauptachse
- Gleichung der Hyperbel in 1. Hauptlage, deren Mittelpunkt nicht der Nullpunkt ist, mit vertikaler Hauptachse
In diesem Artikel sehen wir uns verschiedene Hyperbelgleichungen an und erfahren, wie man sie erhält.
Gleichung der Hyperbel in 1. Hauptlage mit Nullpunkt als Mittelpunkt und horizontaler Hauptachse
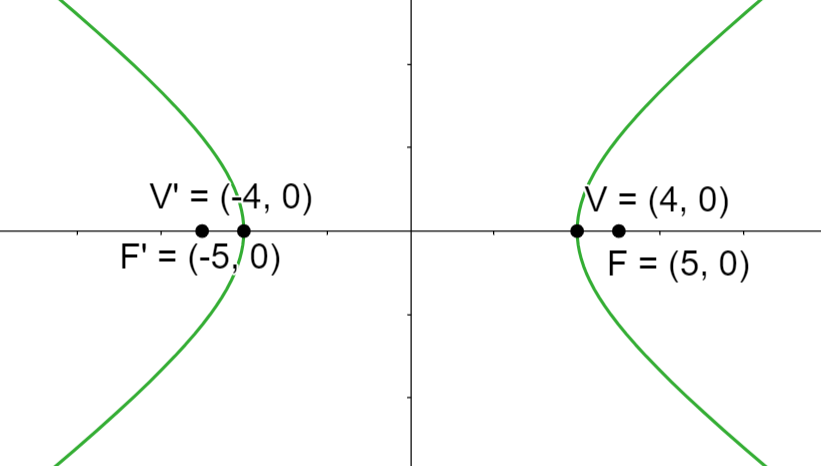
Bei der Gleichung der Hyperbel in 1. Hauptlage stimmen die Achsen der Hyperbel mit den Achsen des Koordinatensystems überein. Somit stimmt der Mittelpunkt der Hyperbel mit dem Nullpunkt der Ebene überein. In diesem Fall betrachten wir die Hauptachse auf der x-Achse.
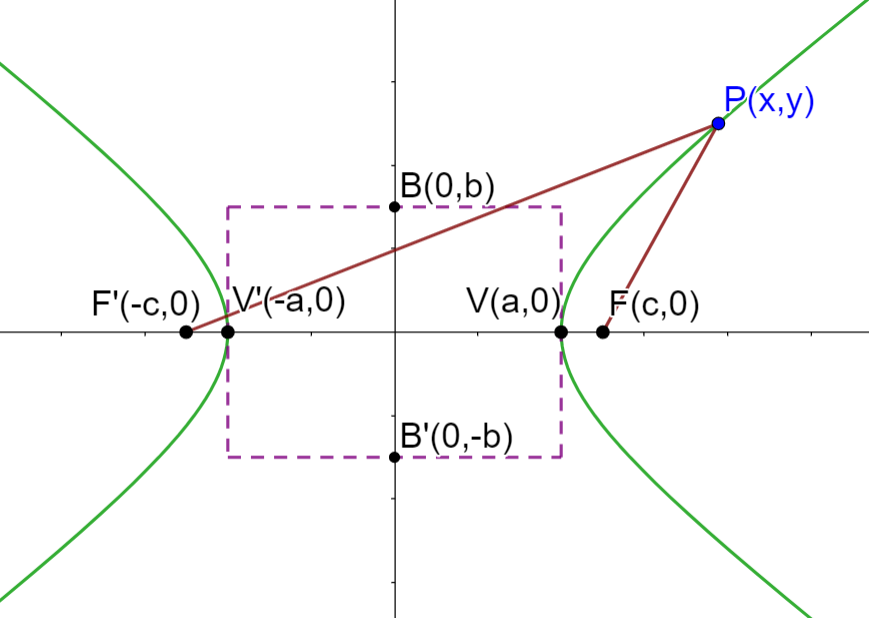
Wir sehen uns die Elemente der in der Abbildung dargestellten Hyperbel und einige Eigenschaften an:
1 Der Mittelpunkt ist der Nullpunkt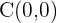 
. Der Mittelpunkt liegt immer in der Mitte zwischen den Scheitelpunkten. Dieser wiederum liegt auf dem Mittelpunkt der Brennpunkte.
2 Scheitelpunkte: Die Scheitelpunkte sind gegeben durch die Punkte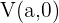 
und 
. Jeder Scheitelpunkt befindet sich im selben Abstand 
zum Mittelpunkt.
3 Brennpunkte: Die Brennpunkte sind gegeben durch die Punkte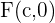 
und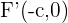 
. Jeder Brennpunkt hat denselben Abstand 
zum Mittelpunkt.
4 Hauptachse: Die Verbindungsgerade zwischen den Scheitelpunkten, nämlich 
. Ihr Wert (Länge) entspricht 
. Diese Achse liegt auf der x-Achse.
5 Nebenachse: Die Verbindungsgerade zwischen den Punkten 
und 
, nämlich 
. Ihr Wert (Länge) entspricht 
. Diese Achse liegt auf der y-Achse.
6 Brennachse: Nebenachse: Die Verbindungsgerade zwischen den Brennpunkten, nämlich 
. Ihr Wert (Länge) entspricht 
.
7 Für die Konstanten , 
und , die die Hyperbel definieren, gilt
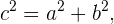
8 Die Exzentrizität der Hyperbel ist gegeben durch
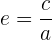
Für jeden Punkt 
muss gelten:
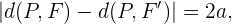
Durch die Definition des euklidischen Abstands wissen wir, dass Folgendes gilt:
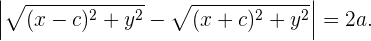
Indem wir bestimmte Rechenoperationen durchführen, können wir die vorhergehende Gleichheit wie folgt ausdrücken
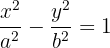
Diese letzte Gleichung ist bekannt als die Gleichung der Hyperbel in 1. Hauptlage mit horizontaler Achse.
Übungsaufgaben
Im weiteren Verlauf sehen wir uns einige Aufgaben an, um unser Wissen praktisch anzuwenden.
Bestimme die Gleichung für eine Hyperbel mit dem Brennpunkt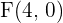 
, dem Scheitelpunkt 
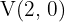und dem Mittelpunkt 
.
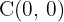Da der Mittelpunkt der Nullpunkt 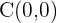ist und der Brennpunkt 
ist, wissen wir, dass 
. Außerdem wissen wir, dass beide Brennpunkte Einheiten vom Mittelpunkt entfernt liegen. Deshalb liegt der andere Brennpunkt bei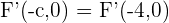 
.
Analog zum Brennpunkt wissen wir, dass ein Brennpunkt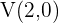 
ist und deshalb 
ist. Da beide Scheitelpunkte Einheiten vom Mittelpunkt entfernt liegen, liegt der andere Scheitelpunkt bei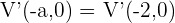 
.
Nun erhalten wir den Wert für . Es gilt Folgendes:
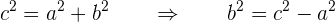
Das heißt:
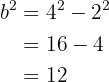
Somit ist 
. Wir haben bereits die Werte für und , die wir benötigen, um unsere Gleichung der Hyperbel in 1. Hauptlage zu erhalten. Diese ist:
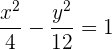
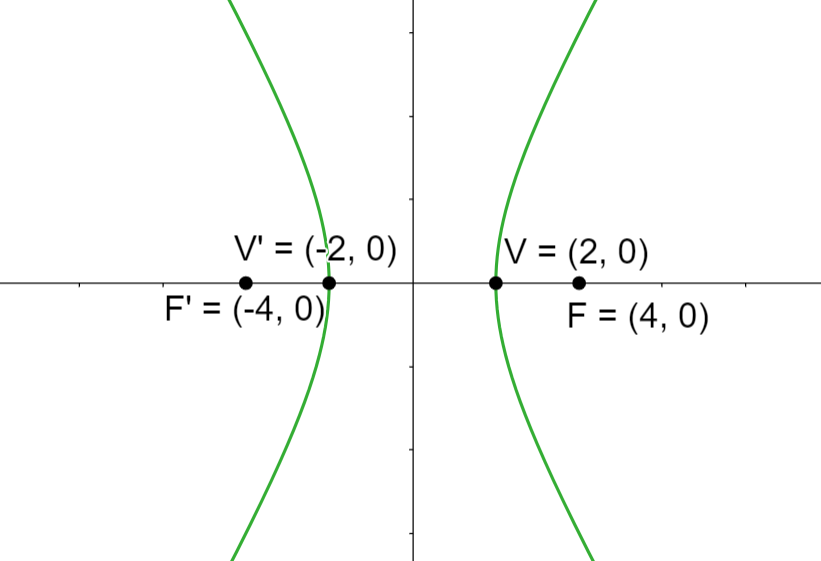
Bestimme die Gleichung und Exzentrizität der Hyperbel, die die Brennpunkte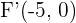 
und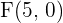 
besitzt sowie eine Hauptachse vom Wert 
.
Da wir bereits die Brennpunkte 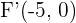und 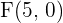haben, ergibt sich 
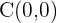. Außerdem sehen wir, dass der Mittelpunkt der Nullpunkt ist.
Die Hauptachse entspricht , wir können somit den Wert für bestimmen
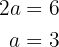
Wir sehen nun sofort, dass die Scheitelpunkte wie folgt gegeben sind
Nun wenden wir die Regel 
an, um den Wert für zu erhalten. Wir erhalten
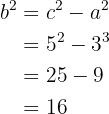
Wir sehen sofort, dass 
ist. Nun wissen wir alles, um die Gleichung der Hyperbel in 1. Hauptlage zu erhalten. Diese ist:
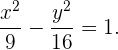
Die Exzentrizität ist
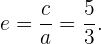
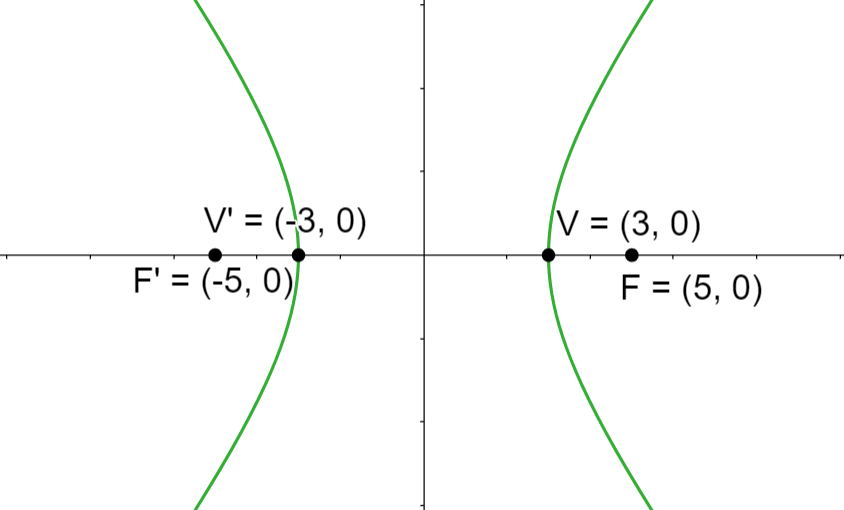
Bestimme die Scheitelpunkte, die Brennpunkte und die Exzentrizität der Hyperpel, die durch folgende Gleichung gegeben ist:
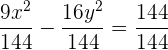
Zunächst müssen wir die Gleichung entsprechend umformen
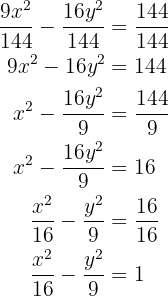
Wir sehen sofort, dass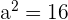 
und somit 
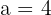ist. Daraus können wir schließen, dass die Scheitelpunkte 
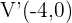und 
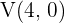sind.
Durch die Gleichung der Hyperbel wissen wir, dass 
und somit 
ist. Somit haben wir bereits und . Wir erhalten
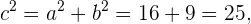
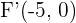Somit ergibt sich . Die Brennpunkte sind und .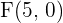
Schließlich ist die Exzentrizität gegeben durch
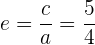
Gleichung der Hyperbel in 1. Hauptlage mit Nullpunkt als Mittelpunkt und vertikaler Hauptachse
In diesem Fall sehen wir uns die Hauptachse auf der y-Achse an.
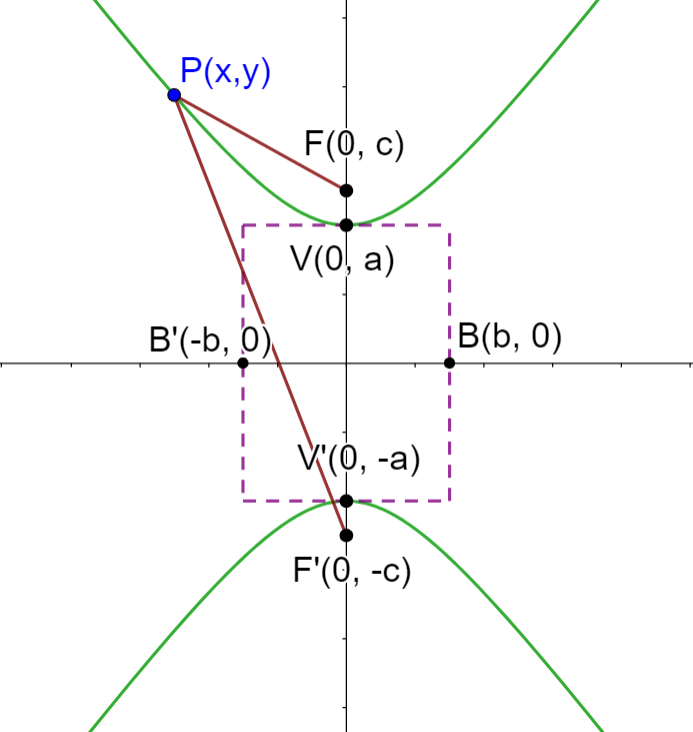
Wir sehen uns die Elemente der in der Abbildung dargestellten Hyperbel und einige Eigenschaften an:
1 Der Mittelpunkt ist der Nullpunkt 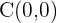. Der Mittelpunkt ist immer der Punkt in der Mitte der Scheitelpunkte, der wiederum mit dem Mittelpunkt der Brennpunkte übereinstimmt.
2 Scheitelpunkte: Die Scheitelpunkte sind gegeben durch die Punkte 
und 
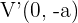. Jeder Scheitelpunkt hat denselben Abstand zum Mittelpunkt.
3 Brennpunkte: Die Brennpunkte sind gegeben durch die Punkte 
und 
. Jeder Brennpunkt hat denselben Abstand zum Mittelpunkt
4 Hauptachse: Die Verbindungsgerade zwischen den Scheitelpunkten, nämlich . Ihr Wert (Länge) entspricht . Diese Achse liegt auf der y-Achse.
5 Nebenachse: Die Verbindungsgerade zwischen den Punkten und , nämlich . Ihr Wert (Länge) entspricht . Diese Achse liegt auf der x-Achse.
6 Brennachse: Nebenachse: Die Verbindungsgerade zwischen den Brennpunkten, nämlich . Ihr Wert (Länge) entspricht .
7 Für die Konstanten , und , die die Hyperbel vollständig definieren, gilt
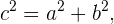
8 Die Exzentrizität der Hyperbel ist gegeben durch
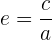
Jeder Punkt auf der Hyperbel muss folgende Bedingungen erfüllen
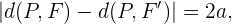
Durch die Definition des euklidischen Abstands zwischen zwei Punkten wissen wir, dass Folgendes gilt:
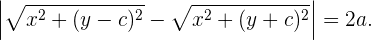
Indem wir bestimmte Rechenoperationen durchführen, können wir die vorhergehende Gleichheit wie folgt darstellen
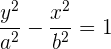
Diese letzte Gleichung ist als Gleichung der Hyperbel in 1. Hauptlage mit vertikaler Achse bekannt.
Übungsaufgaben
Nun sehen wir uns eine weitere Aufgaben an, um unser Wissen auf die Probe zu stellen.
Bestimme die Gleichung der Hyperbel mit dem Brennpunkt 
, dem Scheitelpunkt 
und dem Mittelpunkt .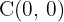
Da der Mittelpunkt der Nullpunkt 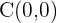ist und ein Brennpunkt ist, wissen wir, dass ist. Außerdem wissen wir, dass beide Brennpunkte im Abstand zum Mittelpunkt liegen. Deshalb ist der andere Brennpunkt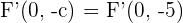 
.
Analog zum Brennpunkt wissen wir, dass ein Scheitelpunkt ist, weshalb ist. Da beide Scheitelpunkte im Abstand zum Mittelpunkt liegen, ist der andere Scheitelpunkt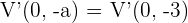 
.
Nun haben wir den Wert für . Es gilt
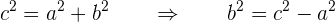
Das heißt
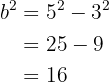
und somit . Wir haben bereits die Werte und , die wir für unsere Gleichung der Hyperbel in 1. Hauptlage haben. Diese ist
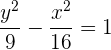
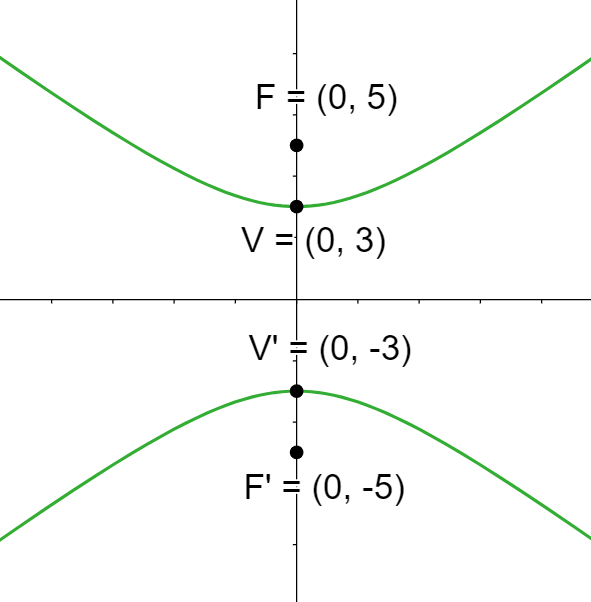
Bestimme die Gleichung der Hyperbel mit dem Mittelpunkt 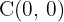, dem Brennpunkt 
und der Nebenachse, die 
entspricht.
Der Mittelpunkt ist der Nullpunkt 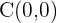und ein Brennpunkt ist . Es gilt daher 
. Außerdem wissen wir, dass beide Brennpunkte im Abstand zum Mittelpunkt liegen. Somit ist der andere Brennpunkt 
.
Wir stellen nun fest, dass die Hauptachse auf der Verbindungsgeraden der Brennpunkte liegt. Dies bedeutet, dass die Hauptachse vertikal ist. Somit ist die Nebenachse vertikal. Außerdem wissen wir, dass die Nebenachse den Wert hat. Es gilt
Nun bestimmen wir den Wert für . Es gilt:
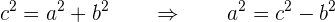
Das heißt
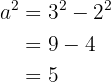
Somit ist 
.
Nun wissen wir, dass die Scheitelpunkte sich im Abstand zum Mittelpunkt befinden. Da die Hauptachse vertikal ist, wissen wir, dass die Scheitelpunkte durch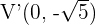 
und 
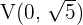gegeben sind.
Wir haben bereits die Werte für und , die wir benötigen, um die Gleichung der Hyperbel in 1. Hauptlage zu erhalten. Diese ist
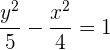
Gleichung der Hyperbel in 1. Hauptlage, deren Mittelpunkt nicht der Nullpunkt ist, mit horizontaler Hauptachse
In diesem Fall ist der Mittelpunkt der Hyperbel nicht der Nullpunkt. Ihre Hauptachse ist horizontal, parallel zur x-Achse.
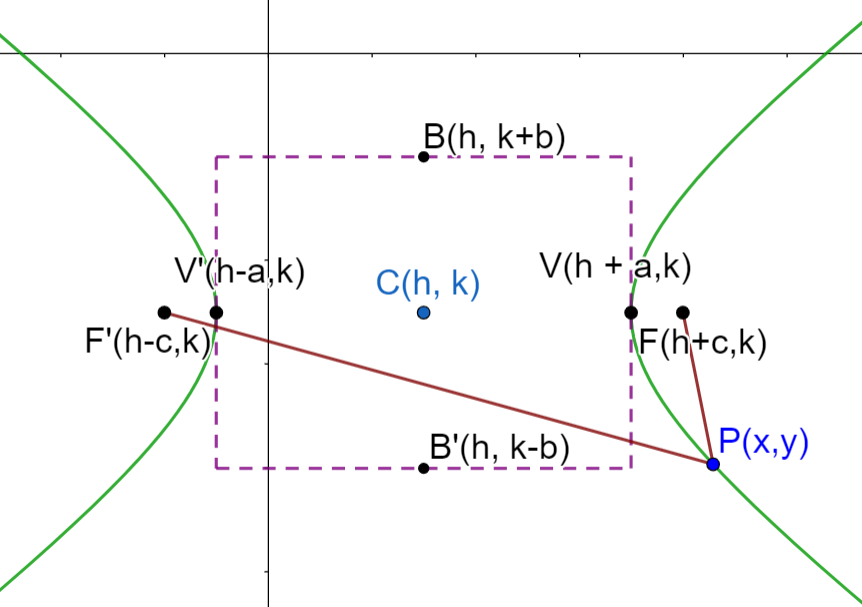
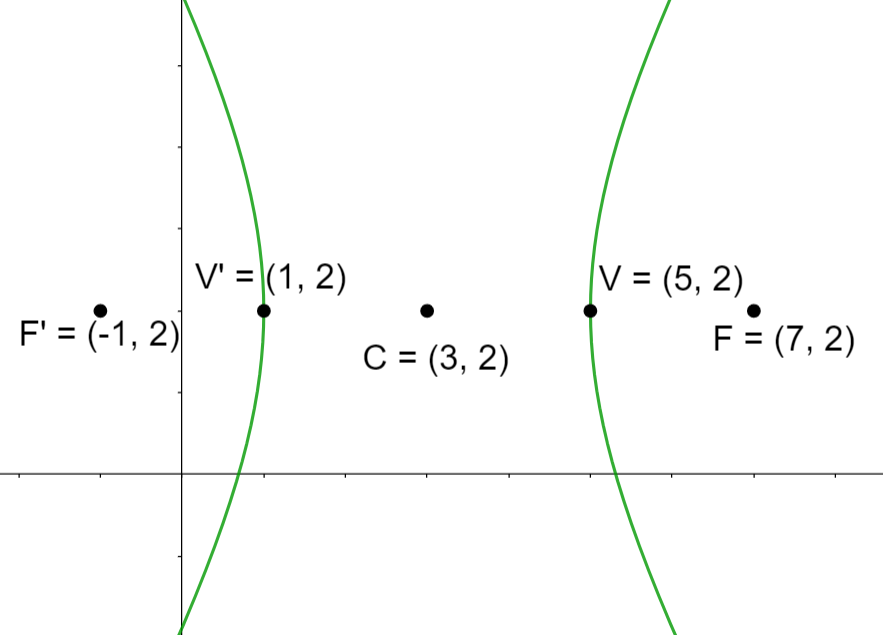
Wir sehen uns die Elemente der in der Abbildung dargestellten Hyperbel und einige Eigenschaften an:
1 Der Mittelpunkt ist der Nullpunkt 
. Der Mittelpunkt ist immer der Punkt in der Mitte der Scheitelpunkte, der wiederum mit dem Punkt in der Mitte der Brennpunkte übereinstimmt.
2 Scheitelpunkte: Die Scheitelpunkte sind durch die Punkte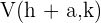 
und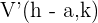 
gegeben. Jeder Scheitelpunkt hat denselben Abstand zum Mittelpunkt.
3 Brennpunkte: Die Brennpunkte sind durch die Punkte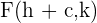 
und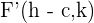 
gegeben. Jeder Brennpunkt hat denselben Abstand zum Mittelpunkt.
4 Hauptachse: Die Verbindungsgerade zwischen den Scheitelpunkten, nämlich . Ihr Wert (Länge) entspricht . Diese Achse ist parallel zur x-Achse.
5 Nebenachse: Die Verbindungsgerade zwischen den Punkten und , nämlich . Ihr Wert (Länge) entspricht . Diese Achse ist parallel zur y-Achse.
6 Brennachse: Nebenachse: Die Verbindungsgerade zwischen den Brennpunkten, nämlich . Ihr Wert (Länge) entspricht .
7 Für die Konstanten , und , die die Hyperbel vollständig definieren, gilt
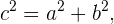
8 Die Exzentrizität der Hyperbel ist gegeben durch
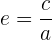
Jeder Punkt auf der Hyperbel muss Folgendes erfüllen
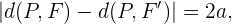
Durch die Definition des euklidischen Abstands zwischen zwei Punkten wissen wir, dass Folgendes gilt:
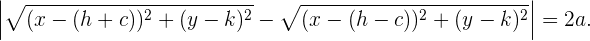
Indem wir bestimmte Rechenoperationen durchführen, können wir die vorhergehende Gleichheit wie folgt darstellen
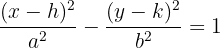
Diese letzte Gleichung heißt Gleichung der Hyperbel in der 1. Hauptlage mit horizontaler Achse und mit einem anderen Mittelpunkt als dem Nullpunkt.
Übungsaufgaben
Wir sehen uns noch ein paar weitere Aufgaben an, um unser Wissen zu vertiefen
Bestimme die Gleichung der Hyperbel mit dem Brennpunkt 
, dem Scheitelpunkt 
und dem Mittelpunkt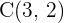 
.
Da der Mittelpunkt der Nullpunkt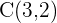 
ist und 
ein Brennpunkt ist, wissen wir, dass
Außerdem wissen wir, dass beide Brennpunkte im Abstand zum Mittelpunkt liegen. Deshalb ist der andere Brennpunkt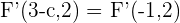 
.
Analog zum Brennpunkt wissen wir, dass ein Nullpunkt ist. Deshalb
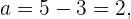
Da beide Scheitelpunkte im Abstand zum Mittelpunkt liegen, ist 
der andere Scheitelpunkt.
Nun erhalten wir den Wert für . Wir wissen, dass gilt
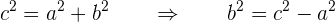
Das heißt
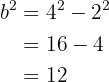
Somit ist . Da wir bereits die Werte für und haben, die wir für unsere Gleichung der Hyperbel in 1. Hauptlage benötigen, lautet diese
Bestimme die Gleichung der Hyperbel mit dem Mittelpunkt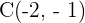 
, einem Abstand zum Brennpunkt von 
und der horizontalen Hauptachse vom Wert .
Da der Mittelpunkt der Nullpunkt 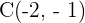ist und die horizontale Hauptachse entspricht, können wir somit unseren Wert für bestimmen.
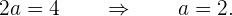
Unsere Scheitelpunkte sind also
und
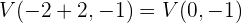
Analog dazu wissen wir, dass die Brennachse ebenfalls horizontal ist (sie verläuft immer wie die Hauptachse, da die Hauptachse innerhalb der Brennachse liegt). Außerdem, da wir einen Wert von haben, nutzen wir diesen, um zu erhalten
Deshalb sind unsere Brennpunkte
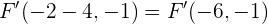
und
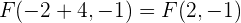
Wir bestimmen nun den Wert für . Wir wissen, dass Folgendes gilt.
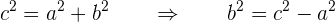
Das heißt
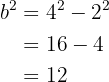
Somit ist . Da wir bereits die Werte für und haben, die wir für die Hyperbelgleichung benötigen, lautet diese
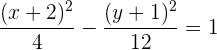
Gleichung der Hyperbel in 1. Hauptlage, deren Mittelpunkt nicht der Nullpunkt ist, mit vertikaler Hauptachse
In diesem Fall ist der Mittelpunkt der Hyperbel nicht der Nullpunkt und ihre Hauptachse ist vertikal, parallel zur y-Achse.
Wir sehen uns die Elemente der in der Abbildung dargestellten Hyperbel und einige Eigenschaften an:
1 Der Mittelpunkt ist der Nullpunkt . Der Mittelpunkt ist immer der Punkt in der Mitte der Scheitelpunkte, der wiederum mit dem Mittelpunkt der Brennpunkte übereinstimmt.
2 Scheitelpunkte: Die Scheitelpunkte sind durch die Punkte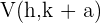 
und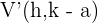 
gegeben. Jeder Scheitelpunkt hat denselben Abstand zum Mittelpunkt.
3 Brennpunkte: Die Brennpunkte sind durch die Punkte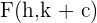 
und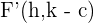 
gegeben. Jeder Brennpunkt hat denselben Abstand zum Mittelpunkt.
4 Hauptachse: Die Verbindungsgerade zwischen den Scheitelpunkten, nämlich . Ihr Wert (Länge) entspricht . Diese Achse ist parallel zur y-Achse.
5 Nebenachse: Die Verbindungsgerade der Punkte und , nämlich . Ihr Wert (Länge) entspricht . Diese Achse ist parallel zur x-Achse.
6 Brennachse: Nebenachse: Die Verbindungsgerade zwischen den Brennpunkten, nämlich . Ihr Wert (Länge) entspricht .
7 Für die Konstanten , und , die die Hyperbel vollständig definieren, gilt
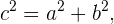
8 Die Exzentrizität der Hyperbel ist gegeben durch
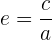
Für jeden Punkt auf der Hyperbel muss gelten
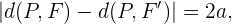
Durch die Definition des euklidischen Abstands zwischen zwei Punkten wissen wir, dass
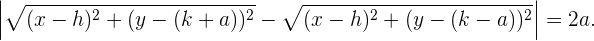
Indem wir bestimmte Rechenoperationen durchführen, können wir die vorhergehende Gleichheit wie folgt ausdrücken
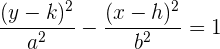
Diese letzte Gleichung heißt Gleichung der Hyperbel in 1. Hauptlage mit vertikaler Achse und mit einem anderen Mittelpunkt als dem Nullpunkt.
Übungsaufgaben
Wir sehen uns noch ein paar weitere Aufgaben an, um unser Wissen praktisch anzuwenden
Bestimme die Gleichung der Hyperbel mit dem Brennpunkt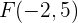 
, dem Scheitelpunkt 
und dem Mittelpunkt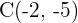 
.
Da der Mittelpunkt der Nullpunkt ist 
ist und 
ein Brennpunkt ist, wissen wir, dass
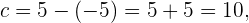
Außerdem wissen wir, dass beide Brennpunkte im Abstand zum Mittelpunkt liegen. Somit ist der andere Brennpunkt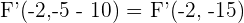 
.
Analog zum Brennpunkt wissen wir, dass ein Scheitelpunkt ist und deshalb
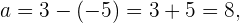
Da beide Scheitelpunkte im Abstand zum Mittelpunkt liegen, ist der andere Scheitelpunkt
.
Wir erhalten nun den Wert für . Es gilt:
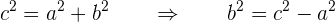
Das heißt
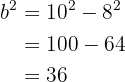
Somit ist 
. Da wir bereits die Werte für und haben, die wir benötigen, um unsere Gleichung der Hyperbel zu erhalten, lautet diese
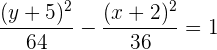
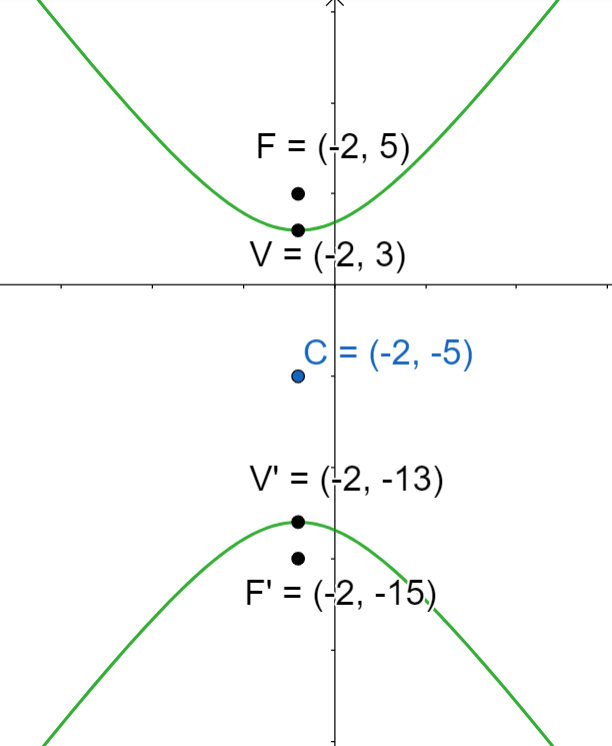
Bestimme die Gleichung der Hyperbel mit dem Mittelpunkt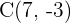 
, der Brennachse mit dem Wert 
und der horizontalen Nebenachse mit dem Wert .
Wir wissen, dass die Brennachse den Wert hat. Somit erhalten wir den Wert für
Deshalb sind die Brennpunkte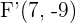 
und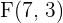 
.
Nun wissen wir, dass die Nebenachse den Wert hat, deshalb
Somit erhalten wir , da
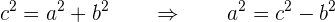
Das heißt
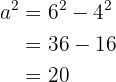
Somit ist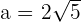 
. Wir haben bereits die Werte für und , die wir benötigen, um unsere Gleichung der Hyperbel zu erhalten. Diese lautet
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
