Bestimme die Gleichung des Kreises, dessen Mittelpunkt im Punkt 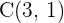 liegt und der die Gerade
liegt und der die Gerade  tangiert.
tangiert.
1 Wir stellen graphisch dar
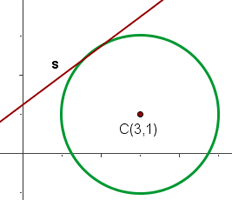
2Der Radius ist immer senkrecht zu einer Tangente des Kreises. Wenn man also den Abstand zwischen dem Mittelpunkt und der Tangente berechnet, erhält man den Radius des Kreises.
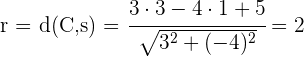
3Wir schreiben die allgemeine Gleichung des Kreises mit dem Mittelpunkt 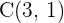 und dem Radius
und dem Radius 

4Wir lösen die quadratischen Terme auf und schreiben die allgemeine Gleichung des Kreises
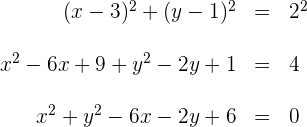
5Somit ist die gesuchte Gleichung

Bestimme die Gleichung des Kreises, der durch die Punkte  und
und  verläuft und seinen Mittelpunkt auf der Geraden
verläuft und seinen Mittelpunkt auf der Geraden  hat.
hat.
1 Wir stellen graphisch dar
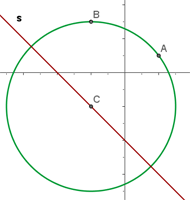
2 Wir stellen den Mittelpunkt mit den Koordinaten 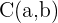 dar. Die allgemeine Gleichung des Kreises ist
dar. Die allgemeine Gleichung des Kreises ist
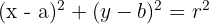
3 Die Punkte  und
und  befinden sich auf dem Kreis und erfüllen somit die folgende Gleichung
befinden sich auf dem Kreis und erfüllen somit die folgende Gleichung
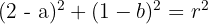
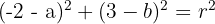
4 Wir setzen die Gleichungen gleich und vereinfachen
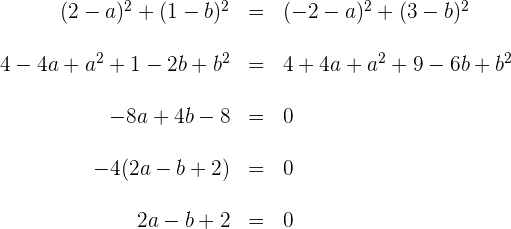
5 Da sich der Mittelpunkt auf der Geraden  befindet, gilt
befindet, gilt

6 Es ergibt sich folgendes Gleichungssystem

7 Die Addition der beiden Gleichungen ergibt
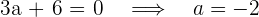
8 Wir setzen in die erste Gleichung des Systems ein und erhalten
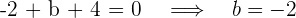
9 Wir setzen die erhaltenen Werte in 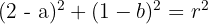 ein und erhalten
ein und erhalten
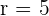
10 Wir setzen die Werte des Mittelpunkts und des Radius in die allgemeine Gleichung des Kreises ein. Wir lösen und erhalten
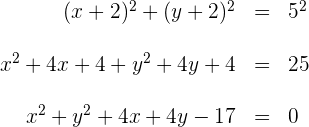
Berechne die Gleichung des Kreises, der durch den Punkt  verläuft, dessen Radius
verläuft, dessen Radius  ist und dessen Mittelpunkt auf der Winkelhalbierenden des ersten und dritten Quadranten liegt.
ist und dessen Mittelpunkt auf der Winkelhalbierenden des ersten und dritten Quadranten liegt.
1 Wir stellen graphisch dar
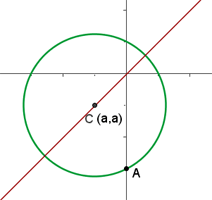
2 Der Mittelpunkt befindet sich auf der Geraden  . Der Mittelpunkt wird also durch
. Der Mittelpunkt wird also durch 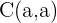 dargestellt. Die allgemeine Gleichung des Kreises ist
dargestellt. Die allgemeine Gleichung des Kreises ist
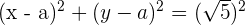
3 Der Punkt 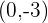 liegt auf dem Kreis, weshalb er die Gleichung erfüllt
liegt auf dem Kreis, weshalb er die Gleichung erfüllt

Es gilt 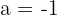 und
und 
4 Die Gleichung des Kreises für 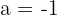 ist
ist
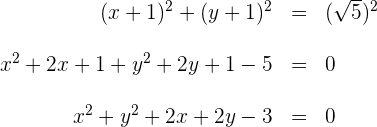
5 Die Gleichung des Kreises für  ist
ist

Berechne die Gleichung des Kreises, der durch den Punkt  verläuft, dessen Radius
verläuft, dessen Radius  ist und dessen Mittelpunkt sich auf der Geraden
ist und dessen Mittelpunkt sich auf der Geraden 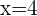 befindet.
befindet.
1 Der Mittelpunkt befindet sich auf der Geraden 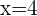 . Der Mittelpunkt wird also durch
. Der Mittelpunkt wird also durch  dargestellt. Die allgemeine Gleichung des Kreises ist
dargestellt. Die allgemeine Gleichung des Kreises ist
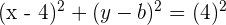
2 Der Punkt  befindet sich auf dem Kreis, sodass er folgende Gleichung erfüllen muss
befindet sich auf dem Kreis, sodass er folgende Gleichung erfüllen muss
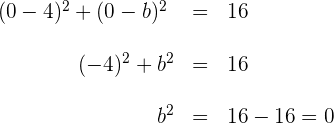
3 Deshalb kommen wir zu dem Ergebnis, dass  . Somit lautet die Gleichung des Kreises für
. Somit lautet die Gleichung des Kreises für  wie folgt
wie folgt

Wenn die Gleichung des Kreises 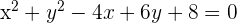 ist, dann misst sein Radius:
ist, dann misst sein Radius:
1 Wir haben die allgemeine Formel des Kreises
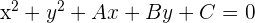
Dieser Gleichung können wir alle notwendigen Werte für unseren Kreis entnehmen.
2 Aus der vorhergehenden Gleichung wissen wir, dass sein Radius durch folgende Gleichung bestimmt ist
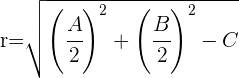
3 In unserem speziellen Fall wissen wir, dass  ,
,  und
und  ist. Indem wir sie ersetzen, erhalten wir unser gesuchtes Ergebnis
ist. Indem wir sie ersetzen, erhalten wir unser gesuchtes Ergebnis
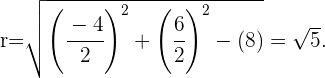
Berechne die Gleichung des Kreises, bei dem einer seiner Durchmesser die Extremwerte 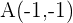 ,
,  hat.
hat.
1 Wenn das Segment  ein Durchmesser des Kreises ist, ist der Mittelpunkt dieses Segments der Radius des Kreises.
ein Durchmesser des Kreises ist, ist der Mittelpunkt dieses Segments der Radius des Kreises.
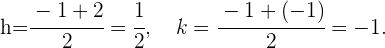
Wir stellen fest, dass der Mittelpunkt des Kreises 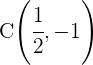 ist.
ist.
2 Um den Radius zu berechnen, müssen wir die Länge des Segments  berechnen. Diese beträgt
berechnen. Diese beträgt

3 Schließlich erhalten wir die Gleichung des Kreises
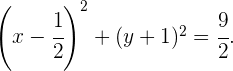
Bestimme die Gleichung des Kreises, dessen Mittelpunkt sich bei 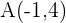 befindet und der die Gerade tangiert, die durch die Punkte
befindet und der die Gerade tangiert, die durch die Punkte  und
und  verläuft.
verläuft.
1 Zunächst berechnen wir die Gleichung der Geraden. Da diese durch  und
und  verläuft, ist ihre Steigung
verläuft, ist ihre Steigung
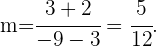
Somit ist die Gleichung der Geraden
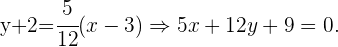
2 Nun betrachten wir den Abstand vom Mittelpunkt zur Tangente, d. h. der Radius ist
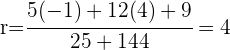
3 Schließlich ist unsere Gleichung
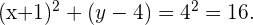
Bestimme die Gleichung eines Kreises, der durch die Punkte  und
und 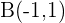 verläuft, und dessen Mittelpunkt sich auf der Geraden
verläuft, und dessen Mittelpunkt sich auf der Geraden 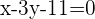 befindet.
befindet.
1 Wir wissen, dass die Gleichung folgende Form hat
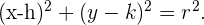
Da der Kreis durch die Punkte  und
und  verläuft, haben wir folgende Gleichung
verläuft, haben wir folgende Gleichung
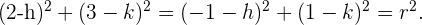
2 Da sich der Mittelpunkt  auf der Geraden der Gleichung
auf der Geraden der Gleichung 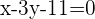 befindet, erhalten wir somit die Gleichung
befindet, erhalten wir somit die Gleichung
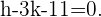
3 Lösen wir die obigen Gleichungen für 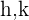 , ergibt sich
, ergibt sich

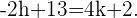
Aus dieser Gleichung und der Gleichung aus 2 ergibt sich

4 Ersetzen wir diese Werte in der Gleichung des Kreises durch einen der Werte, durch die der Kreis verläuft, so erhalten wir den Radius
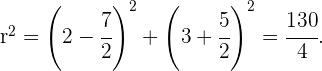
5 Schließlich lautet unsere Gleichung
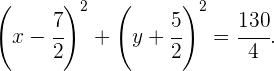
Mit KI zusammenfassen:



