
Die Hyperbel und ihre Elemente
Zunächst sollten wir ein wenig über die Hyperbel sprechen. Die Hyperbel ist der geometrische Ort der Punkte der Ebene, deren Abstandsdifferenz zu den Fixpunkten, den sogenannten Brennpunkten, im Betrag konstant ist.
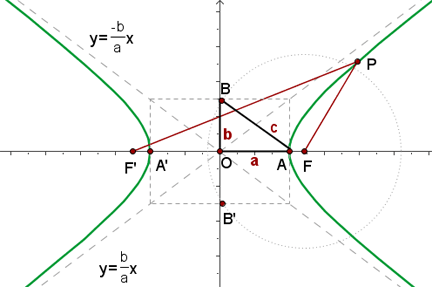
In der Abbildung sehen wir, dass 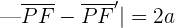 für einen beliebigen Punkt
für einen beliebigen Punkt  der Hyperbel.
der Hyperbel.
Elemente der Hyperbel
1 Brennpunkte: Die Fixpunkte  und
und  .
.
2 Brennachse: Gerade, die durch die Brennpunkte verläuft.
3 Nebenachse: Mittelsenkrechte des Segments  .
.
4 Mittelpunkt: Schnittpunkt der Achsen.
5 Scheitelpunkte: Die Punkte  und
und  sind die Schnittpunkte der Hyperbel mit der Brennachse.
sind die Schnittpunkte der Hyperbel mit der Brennachse.
6 Ortsvektoren: Die Abschnitte zwischen einem Punkt auf der Hyperbel und den Brennpunkten  und
und  .
.
7 Brennstrecke: Abschnitt 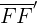 mit der Länge
mit der Länge  .
.
8 Hauptachse: Abschnitt  mit der Länge
mit der Länge  .
.
9 Nebenachse: Abschnitt  mit der Länge
mit der Länge  . Die Punkte
. Die Punkte  und
und  ergeben sich aus dem Schnittpunkt der Nebenachse mit dem Kreis, dessen Mittelpunkt einer der Scheitelpunkte ist und der den Radius
ergeben sich aus dem Schnittpunkt der Nebenachse mit dem Kreis, dessen Mittelpunkt einer der Scheitelpunkte ist und der den Radius  hat.
hat.
10Symmetrieachsen: Die Geraden, die die Haupt- oder Nebenachse enthalten.
11Asymptoten: Geraden der Gleichungen 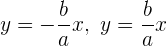
12Verhältnis zwischen den Halbachsen: 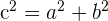
Exzentrizität der Hyperbel
Die Exzentrizität ist ein Parameter, der die Öffnung der Hyperbel anzeigt. Diese Zahl ist im Fall von Hyperbeln immer größer als  .
.
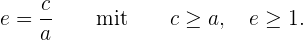
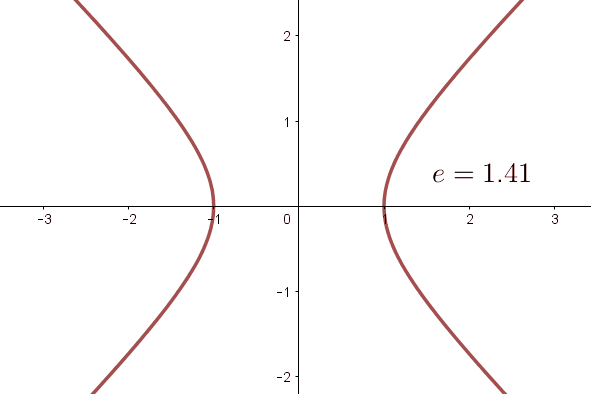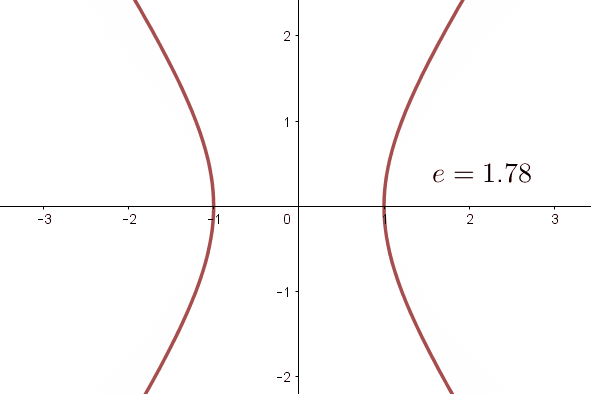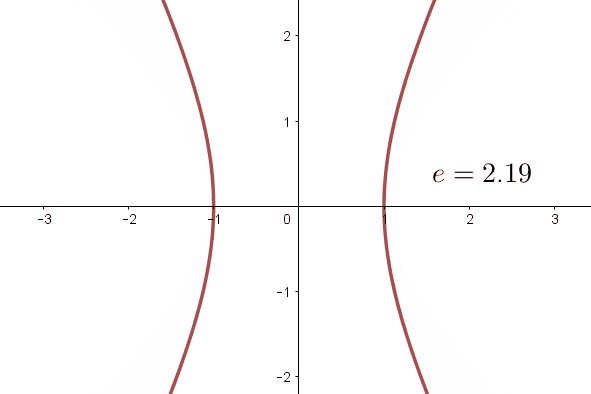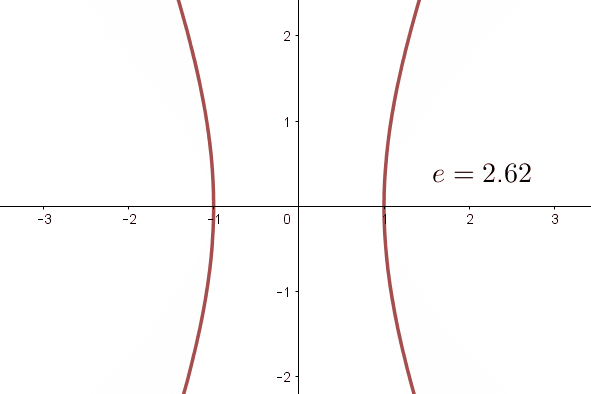
Weitere Informationen zur Exzentrizität der Hyperbel findest du hier hier.
Gleichseitige Hyperbel
Hyperbeln, bei denen die Halbachsen gleich sind, nennt man gleichseitige Hyperbeln. Somit  .
.
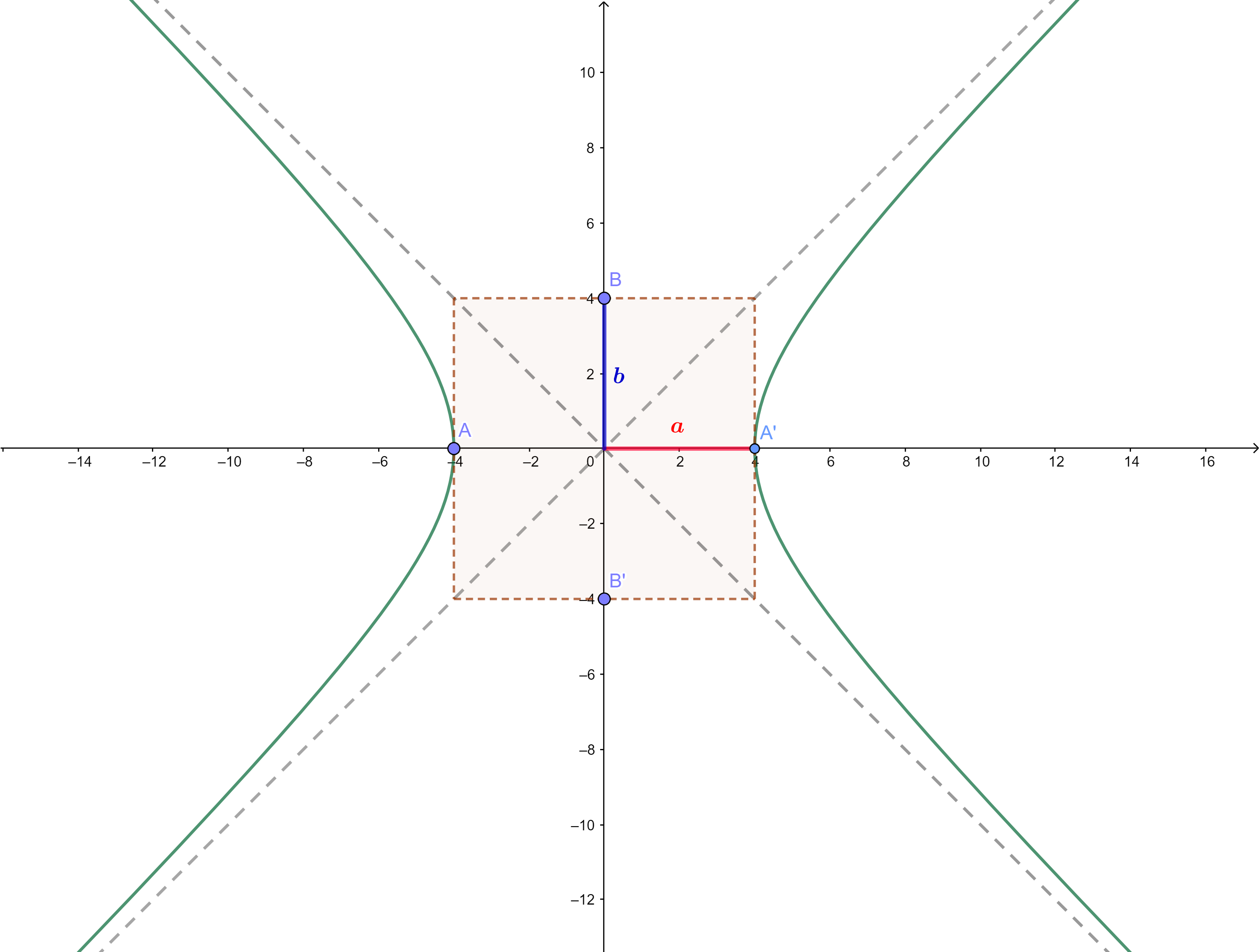
In diesem Fall hat die Hyperbel (im Ursprung zentriert) die folgenden Elemente:
- Ihre Gleichung lautet:
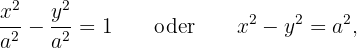
- Ihre Asymptoten sind:
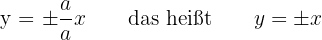 ,
,
weshalb die Asymptoten die Winkelhalbierenden der Quadranten sind. - Ihre Exzentrizität ist gegeben durch:
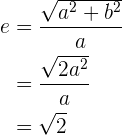
Gleichung der gleichseitigen Hyperbel mit Bezug auf ihre Asymptoten
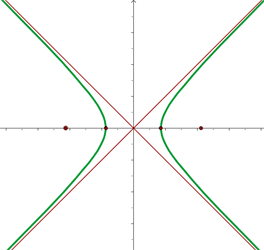
Wenn wir nun von den Achsen  zu den Achsen übergehen wollen, die durch die Asymptoten der gleichseitigen Hyperbel bestimmt sind, dann genügt eine Drehung von
zu den Achsen übergehen wollen, die durch die Asymptoten der gleichseitigen Hyperbel bestimmt sind, dann genügt eine Drehung von  um den Koordinatenursprung.
um den Koordinatenursprung.
Es sei daran erinnert, dass die Koordinaten eines Punktes 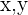 nach einer Drehung um einen Winkel
nach einer Drehung um einen Winkel  durch
durch 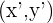 gegeben sind, wobei
gegeben sind, wobei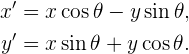
Die Gleichung der gleichseitigen Hyperbel nach einer Drehung um  lautet demnach
lautet demnach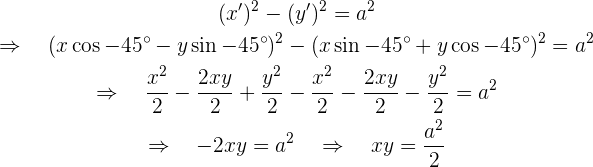
Das heißt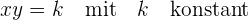 .
.
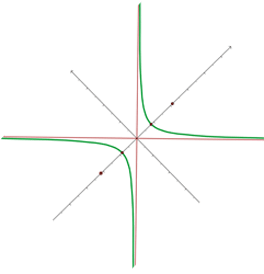
Wenn wir statt einer Drehung um  eine Drehung um
eine Drehung um 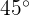 auf den Achsen vornehmen, liegt die Hyperbel im 2. und 4. Quadranten und ihre Gleichung lautet:
auf den Achsen vornehmen, liegt die Hyperbel im 2. und 4. Quadranten und ihre Gleichung lautet: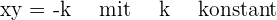
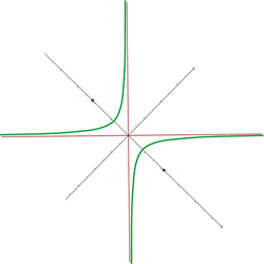
Übung zu einer gleichseitigen Hyperbel
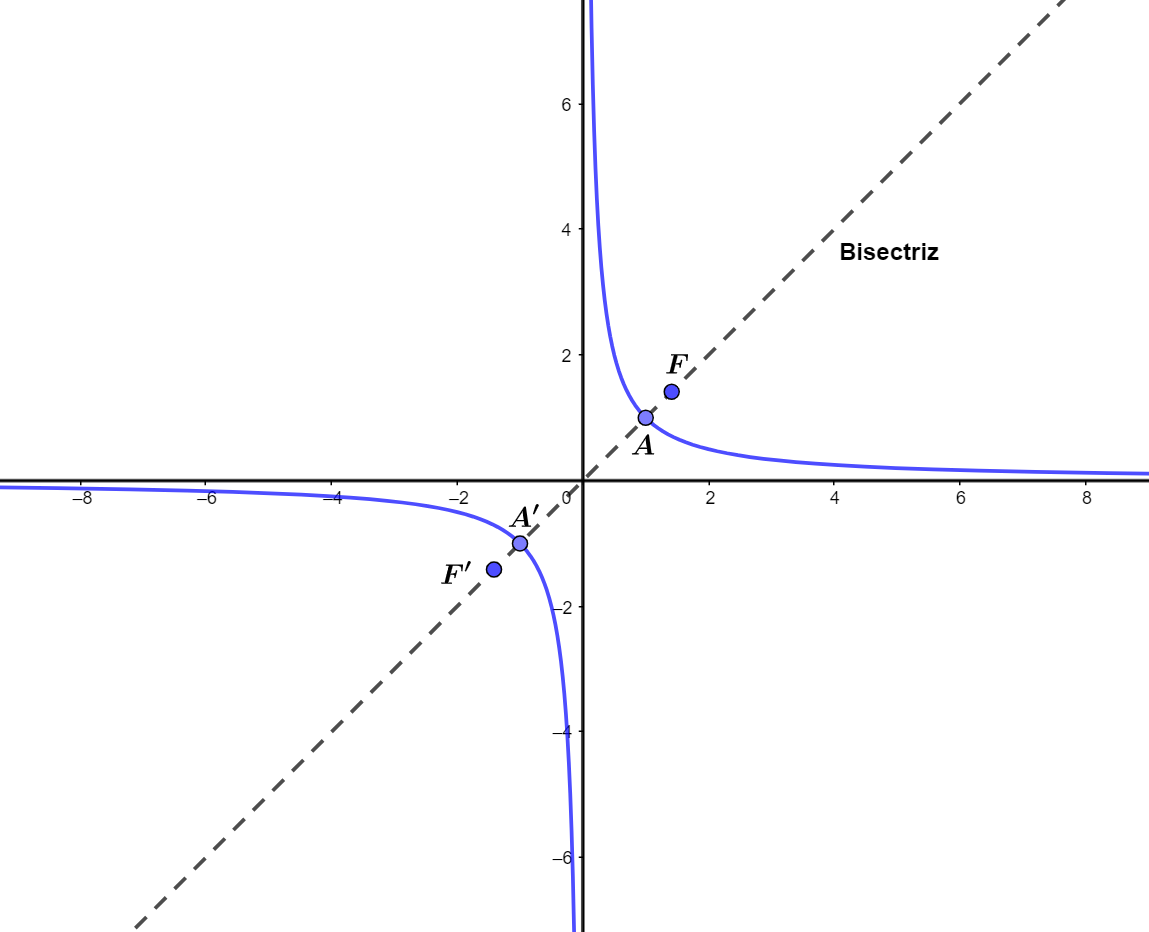
Die Gleichung 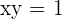 stellt eine gleichseitige Hyperbel dar. Berechne ihre Scheitelpunkte und ihre Brennpunkte.
stellt eine gleichseitige Hyperbel dar. Berechne ihre Scheitelpunkte und ihre Brennpunkte.
Da es sich um eine Hyperbel wie in  handelt, liegen die Koordinaten der Scheitelpunkte
handelt, liegen die Koordinaten der Scheitelpunkte 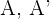 auf der Winkelhalbierenden des 1. und 3. Quadranten, was bedeutet, dass die ersten und zweiten Koordinaten der Scheitelpunkte gleich sind. An den Scheitelpunkten gilt also
auf der Winkelhalbierenden des 1. und 3. Quadranten, was bedeutet, dass die ersten und zweiten Koordinaten der Scheitelpunkte gleich sind. An den Scheitelpunkten gilt also 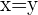 . Andererseits gilt aber auch, dass die Scheitelpunkte zum Graphen gehören, so dass
. Andererseits gilt aber auch, dass die Scheitelpunkte zum Graphen gehören, so dass 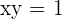 gelten muss. Nimmt man diese beiden letzten Bedingungen zusammen, so ergibt sich:
gelten muss. Nimmt man diese beiden letzten Bedingungen zusammen, so ergibt sich: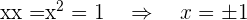
und daraus folgt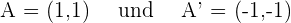 . Für die Brennpunkte beginnen wir mit der Berechnung von
. Für die Brennpunkte beginnen wir mit der Berechnung von  und
und  . Da
. Da  der Abstand zwischen dem Ursprung und dem Scheitelpunkt ist, ergibt sich unter Verwendung der Formel für den Abstand zwischen zwei Punkten Folgendes:
der Abstand zwischen dem Ursprung und dem Scheitelpunkt ist, ergibt sich unter Verwendung der Formel für den Abstand zwischen zwei Punkten Folgendes: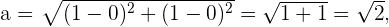
Es handelt sich um eine gleichseitige Hyperbel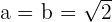
und unter Verwendung der Beziehung zwischen den Halbachsen: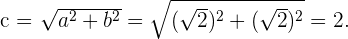 Nun befinden sich die Brennpunkte in einem Abstand
Nun befinden sich die Brennpunkte in einem Abstand  vom Ursprung. Deshalb:
vom Ursprung. Deshalb: 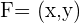
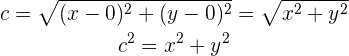
Außerdem liegen die Brennpunkte auch auf der Winkelhalbierenden des 1. und 3. Quadranten, so dass für  und
und 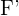 gilt, dass
gilt, dass 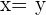 . In Anbetracht des oben Gesagten:
. In Anbetracht des oben Gesagten: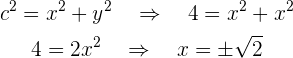
daraus folgt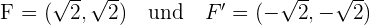
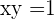 .
.
Mit KI zusammenfassen:












