Graph einer Funktion
Graph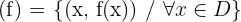 
Um eine Funktion darzustellen, untersuchen wir die verschiedenen Arten von Funktionen sowie deren Definitionsbereich.
Definitionsbereich einer Funktion
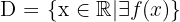
Definitionsbereich einer Polynomfunktion
Der Definitionsbereich einer Polynomfunktion ist die gesamte reelle Achse, also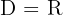 
.
Definitionsbereich einer rationalen Funktion
Eine rationale Funktion hat die Form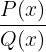 
, donde 
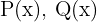Polynome sind. Der Definitionsbereich ist 
minus die Werte, für die der Nenner 0 wird. Also 
.
Definitionsbereich einer Wurzelfunktion mit ungeradem Wurzelexponenten
Eine Wurzelfunktion hat die Form 
. Wenn 
ungerade ist, lautet der Definitionsbereich .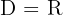
Definitionsbereich einer Wurzelfunktion mit geradem Wurzelexponenten
Eine Wurzelfunktion hat die Form . Wenn gerade ist, besteht der Definitionsbereich aus allen Werten, für die der Radikand größer oder gleich 0 wird. Also 
Definitionsbereich einer Logarithmusfunktion
Eine Logarithmusfunktion hat die Form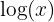 
. Der Definitionsbereich besteht aus allen Werten, für die der Radikand größer oder gleich 0 wird. Also .
Definitionsbereich einer Exponentialfunktion
Eine Exponentialfunktion hat die Form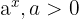 
, wobei 
eine Konstante ist; der Definitionsbereich ist .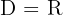
Defintionsbereich einer Sinusfunktion
Der Definitionsbereich einer Sinusfunktion ist .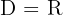
Definitionsbereich einer Kosinusfunktion
Der Definitionsbereich einer Kosinusfunktion ist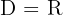
Definitionsbereich einer Tangensfunktion
Der Definitionsbereich einer Tangensfunktion ist
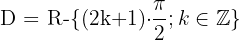
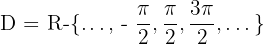
Definitionsbereich einer Kotangensfunktion
Der Definitionsbereich einer Kotangensfunktion ist:
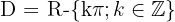
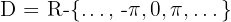
Definitionsbereich einer Sekansfunktion
Der Definitionsbereich einer Sekansfunktion ist:
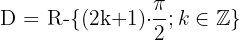
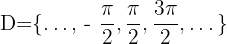
Definitionsbereich einer Kosekansfunktion
Der Definitionsbereich einer Kosekansfunktion ist:
Definitionsbereich beim Rechnen mit Funktionen
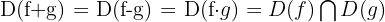
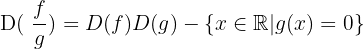
Symmetrie
Symmetrie in Bezug auf die Ordinatenachsen
Gerade Funktion
Um zu wissen, ob eine Funktion gerade ist, muss folgende Bedingung erfüllt sein: 
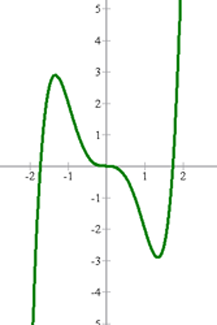
Beispiel:
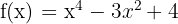
Um herauszufinden, ob eine Funktion gerade ist, müssen wir die Funktion für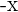 
auswerten. Das heißt, 
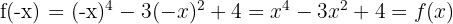. Somit ist die Bedingung einer geraden Funktion erfüllt. Die Grafik zeigt uns die Symmetrie zur y-Achse.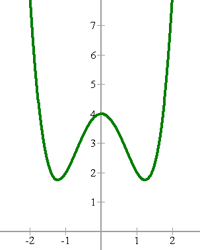
Symmetrie zum Ursprung
Ungerade Funktion
Um zu wissen, ob eine Funktion ungerade ist, muss folgende Bedingung erfüllt sein: 
Beispiel:
Um herauszufinden, ob die Funktion ungerade ist, müssen wir die Funktion für 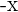auswerten. Das heißt, 
. Somit ist die Bedingung erfüllt, dass es sich um eine ungerade Funktion handelt.
Periodizität
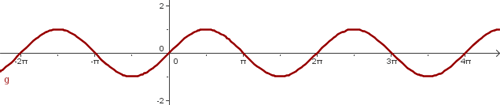
Die Funktion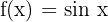 
ist periodisch mit der Periode 
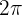. Somit gilt:
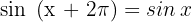
Wenn 
periodisch mit der Periode T ist, so ist es auch 
: die Periode ist 
.
Schnittpunkte mit den Achsen
Schnittpunkte mit der x-Achse
Um die Schnittpunkte mit der x-Achse zu bestimmen, nehmen wir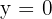 
und lösen die resultierende Gleichung.
Schnittpunkte mit der y-Achse
Um die Schnittpunkte mit der y-Achse zu bestimmen, nehmen wir 
und berechnen den Wert von 
.
Beispiele zu Schnittpunkten mit den Achsen
Asymptoten
Horizontale Asymptoten
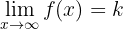
oder
,
wobei y = k
Vertikale Asymptoten
,
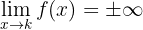wobei x = k
Schiefe Asymptoten
Die Asymptoten haben die Form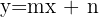 
. Somit
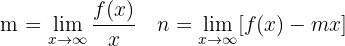
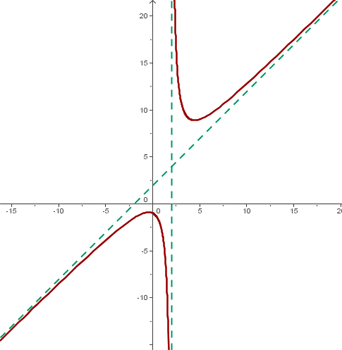
Beispiel
Berechne die Asymptoten der Funktion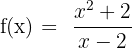 
Horizontale Asymptoten Wir stellen fest, dass wenn wir den Grenzwert berechnen, dieser unendlich ist: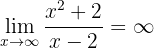 
Deshalb gibt es keine horizontalen Asymptoten. Vertikale Asymptoten Hier ist der Grenzwert 
Somit ist die vertikale Asymptote 
. Schiefe Asymptoten Wir lösen die entsprechenden Grenzwerte nach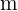 
und auf.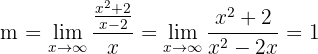 
Somit ist die Asymptote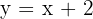 
Parabeläste
Es gibt Parabeläste, wenn:
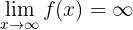
oder
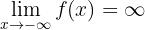
Parabelast in Richtung der y-Achse
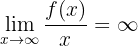
Parabelast in Richtung der x-Achse
Monotonieverhalten
Um das Monotonieverhalten zu untersuchen, befolgen wir folgende Schritte:
1 Funktion ableiten:
2 Die Nullstellen der 1. Ableitung berechnen. Hierfür nehmen wir: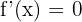 
.
3 Wir bilden offene Intervalle mit den Nullen (Nullstellen) der 1. Ableitung und den Punkten, an denen die Funktion nicht stetig ist (sofern vorhanden)
4 Wir nehmen einen Wert auf jedem Intervall und ermitteln das Vorzeichen, das er in der 1. Ableitung hat.
5 Wir schreiben die Intervalle, auf denen die Funktion fällt oder steigt.
Relative Maxima und Minima
Um die relativen Extrema zu ermitteln, befolgen wir folgende Schritte:
1 Wir ermitteln die 1. Ableitung und berechnen ihre Nullstellen.
2 Wir ermitteln die 2. Ableitung und berechnen das darin enthaltene Vorzeichen aus den Nullstellen der 1. Ableitung. Wenn:
ist ein relatives Maximum
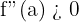ist ein relatives Minimum
3 Wir berechnen die Abbildung (auf die Funktion) der relativen Extrema.
Nach der Untersuchung des Monotonieverhalten gibt es:
1 Ein Maximum an dem Punkt der Funktion, an dem die Funktion von steigend zu fallend übergeht.
2 Ein Minimum an dem Punkt der Funktion, an dem die Funktion von fallend zu steigend wechselt.
Konkavität und Konvexität
Um die Konkavitäts- und Konvexitätsintervalle einer Funktion zu berechnen, gehen wir wie folgt vor:
1 Wir ermitteln die 2. Ableitung und berechnen ihre Nullstellen.
2 Wir bilden offene Intervalle mit den Nullen (Nullstellen) der 2. Ableitung und den Unstetigkeitsstellen (falls vorhanden).
3 Wir nehmen einen Wert auf jedem Intervall und ermitteln das Vorzeichen, das er in der 2. Ableitung hat.
4 Wir schreiben die Intervalle.
Wendepunkte
Para hallar los puntos de inflexión, seguiremos los siguientes pasos:
1 Wir ermitteln die 2. Ableitung und berechnen ihre Nullstellen.
2 Wir führen die 3. Ableitung durch und berechnen das Vorzeichen, das die Nullstellen der 2. Ableitung darin annehmen. Wenn:
Wir haben einen Wendepunkt.
3 Wir berechnen die Abbildung (auf die Funktion) des Wendepunkts.
Da wir bereits die Konkavität und Konvexität einer Funktion untersucht haben, gibt es:
Einen Wendepunkt an dem Punkt der Funktion, an dem die Funktion von konkav zu konvex oder umgekehrt übergeht.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
