Kapitel
Was ist das Unendliche und wie werden Aufgaben mit Grenzwerten gelöst?
Wenn wir es mit Grenzwerten zu tun haben, müssen wir den Begriff Unendliches kennen. Beachte, dass das Unendliche keine bestimmte Zahl darstellt. In manchen Fällen werden wir es wie eine Zahl behandeln, um Grenzwerte zu finden, dennoch müssen wir im Hinterkopf behalten, dass sich das Unendliche in vielen Fällen nicht wie eine normale Zahl verhält.
Es gibt Fälle, in denen Rechenoperationen mit dem Unendlichen unbestimmt sind. Dann verhält sich 
nicht wie eine Zahl. Bei diesen unbestimmten Rechenoperationen müssen wir die Funktion, deren Grenzwert wir berechnen wollen, leicht abwandeln, damit keine unbestimmte Funktion mehr vorliegt. Das Vorgehen wird auch "elementare Umformung" genannt.
Das Epsilon-Delta-Kriterium für Grenzwerte besagt:
Ein Wert 
ist der Grenzwert der Funktion 
an 
, wenn für alle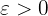 
ein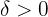 
besteht, für das jedes 
mit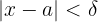 
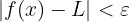erfüllt.
Um zu beweisen, dass der Grenzwert für eine Funktion für einen bestimmten Wert von existiert, überprüft man, ob die in der Definition genannten Kriterien erfüllt werden.
Grenzdefinition: Aufgaben
Überprüfe anhand des Epsilon-Delta-Kriteriums:
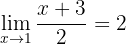
Wir betrachten einen beliebigen Wert für 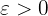. Zu beweisen ist, dass ein 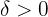existiert, das die Definition des Grenzwerts erfüllt.
Mit
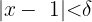
(bisher noch unbekannt) muss erfüllt sein, dass:
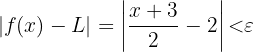
Durch Vereinfachen erhalten wir:
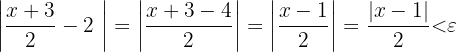
Versuche,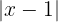 
auf eine Seite der Ungleichung zu bringen, um einen Ausdruck für 
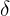zu erhalten. Durch Multiplizieren beider Seiten der Ungleichung mit 2 erhalten wir:
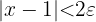
Für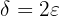 
geht die Ungleichung also auf. Daher ist der geforderte Beweis erbracht.
Was bedeutet das genau?
Es bedeutet, dass es für jeden Wert von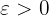 
, den wir betrachten, einen Wert 
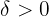finden können, der die Definition erfüllt, da wir hierfür die Formel (in dem Fall —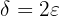]) aufgestellt haben.
Wenn zum Beispiel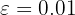 
, gegeben wäre, würden wir 
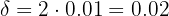erhalten. Daher wäre 
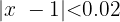gleich
.
D.h.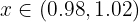 
. Für jeden beliebigen Wert 
im Intervall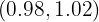 
würde gelten:
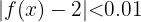
Z.B. wäre für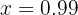 
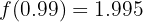. Folglich:
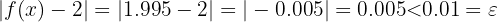
Ähnlich wäre für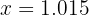 
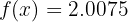. Folglich:
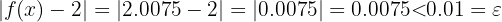
Betrachte den Graphen der Funktion und gebe die gesuchten Grenzwerte an:
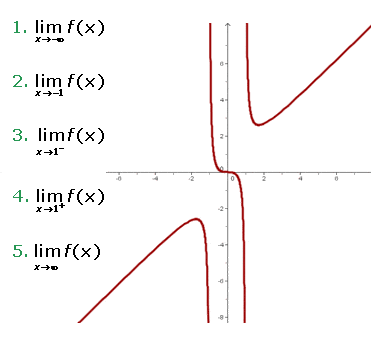
Funktionsgraph der Grenzwerte[/caption]
1 Der erste gesuchte Grenzwert ist
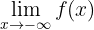
Wenn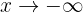 
, d.h. wenn unendlich abnimmt, fällt auch die Funktion unendlich weit ab. Folglich:
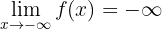
2Bestimme nun
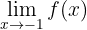
Wir können beobachten, dass die Funktion ins Unendliche abnimmt, wenn sich auf der linken Seite an 
annähert. Wenn sich auf der rechten Seite an annähert, steigt die Funktion dagegen ins Unendliche an. Daher können wir schlussfolgern, dass kein Grenzwert besteht.
3 Berechne nun
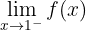
Hier wird der linksseitige Grenzwert betrachtet. Wir können beobachten, dass die Funktion ins Unendliche abnimmt, wenn sich von der linken Seite 
annähert. Der Grenzwert ist also
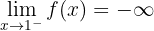
4 Der vierte Grenzwert ist
Hier wird der rechtsseitige Grenzwert betrachtet. Folglich:
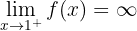
5 Ermittle abschließend den Grenzwert
Dieser ist dem ersten Beispiel sehr ähnlich. Man kann beobachten, dass ins Unendliche ansteigt. nimmt auch ins Unendliche zu. Folglich:
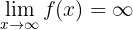
Berechne den Grenzwert:
Gesucht wird der Grenzwert
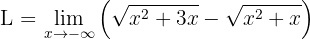
Wenn wir den Limes gegen Unendlich betrachten, erhalten wir eine unbestimmte Form:
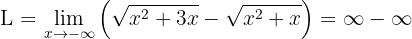
Da der Wert von 
unbestimmt ist, müssen wir die Funktion algebraisch umformen.
Bevor wir mit der algebraischen Umformung starten, wandeln wir den Grenzwert um, indem wir uns seine Eigenschaften zu Nutzen machen:
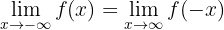
Der Grenzwert ist also:
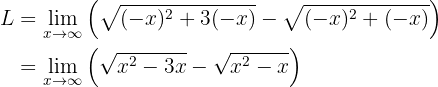
Um die Subtraktion mit Unendlich zu entfernen, wandeln wir nun die Grenzwerte um: Die gelingt durch Rationalisieren (d.h. Multiplizieren und Dividieren durch die konjugiert komplexe Zahl):
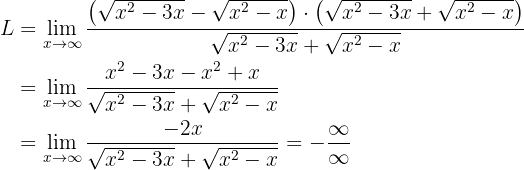
Wenn wir das Globalverhalten der Funktion, also das Verhalten der Funktion gegen Unendlich, anschauen, erhalten wir wieder eine unbestimmte Funktion. In diesem Fall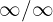 
. Um diese Unbestimmtheit zu entfernen, müssen wir erneut algebraisch umformen. Wir multiplizieren und teilen in diesem Fall durch 
:
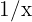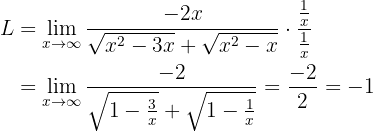
Wir haben das gesuchte Ergebnis erhalten.
Berechne den Grenzwert:
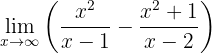
Gesucht wird der Grenzwert:
Wenn wir den Limes gegen Unendlich betrachten, erhalten wir:
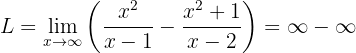
Um den unbestimmten Ausdruck umzuwandeln, können wir hier die Brüche summieren, indem wir den gemeinsamen Nenner bestimmen
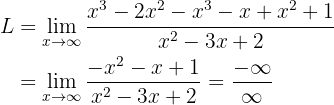
Nun liegt uns der unbestimmte Ausdruck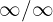 
vor. Wir versuchen, ihn durch Multiplizieren und Dividieren durch einen geeigneten Wert umzuwandeln. Als geeigneter Term bietet sich das Monom höheren Grades im Zähler oder Nenner an, d.h. hier 
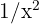. Wir erhalten also:
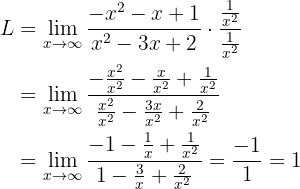
Der Grenzwert ist daher .
Berechne den Grenzwert:
Wenn wir den Limes gegen Unendlich betrachten, erhalten wir:
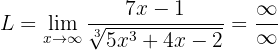
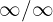ist ein unbestimmter Ausdruck. Wir formen daher wieder durch Multiplizieren und Dividieren durch das Monom des höheren Grades (im Zähler oder Nenner) um. In diesem Fall nehmen wir 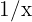— da der Nenner eine Wurzel dritten Grades enthält, kann das "Monom" 
als Monom ersten Grades gelten—. Wir erhalten:
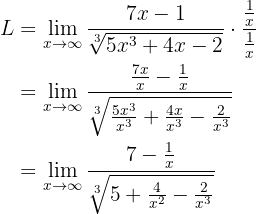
Gegen Unendlich betrachtet erhalten wir:
Ermittle den Grenzwert:
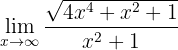
Wenn wir die Funktion gegen Unendlich betrachten, erhalten wir:
Da der Ausdruck unbestimmt ist, formen wir wieder durch Multiplizieren und Dividieren durch das Monom des höheren Grades (
um (beachte, dass die Potenzen des Zählers durch 2 geteilt werden müssen, da sie in einer Quadratwurzel stehen):
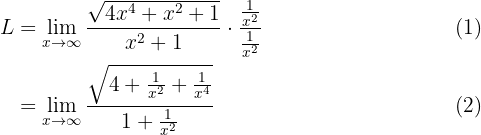
Gegen Unendlich betrachtet erhalten wir:
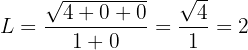
Der Grenzwert ist also 2.
Berechne den Grenzwert:
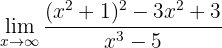
Wenn wir die Funktion gegen Unendlich betrachten, können wir feststellen, dass:
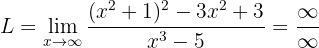
Wir müssen die Funktion also umformen, um den unbestimmten Ausdruck zu entfernen.
Wir können die Aufgabe auf 2 Arten lösen:
1 Durch Vergleichen des Verhaltens im Unendlichen:
Zuerst lösen wir das Binom zum Quadrat auf und erhalten:
Im Zähler erhalten wir 
und im Nenner als Term mit dem höchsten Grad. Der Grad des Zählers ist höher, daher ist unser Grenzwert . Wenn der Grad im Zähler der höhere ist, ist der Grenzwert immer dann , wenn die Terme höheren Grades dasselbe Vorzeichen haben.
2 Durch Dividieren des Zählers und Nenners durch den Term höheren Grades:
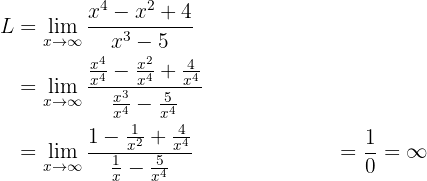
In der Regel ist 
ein unbestimmter Ausdruck. Wir erhalten aber einen Grenzwert für 
. Außerdem sind sowohl der Zähler als auch der Nenner mit Zunahme von zunehmend positiv, daher können wir schließen, dass der Grenzwert ist.
Berechne den Grenzwert:
Wenn wir die Funktion gegen Unendlich betrachten, erhalten wir:
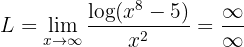
Das Unendliche des Nenners hat jedoch einen höheren Rang. Daher können wir schlussfolgern, dass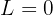 
ist.
Zu bewiesen, dass der Grenzwert 0 ist, ohne die Regel von L´Hospital oder die Regel des höheren Grades anzuwenden, ist jedoch kompliziert. Man kann wie folgt vorgehen:
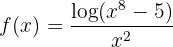
Um den Grenzwert zu ermitteln, müssen wir zwei Funktionen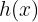 
und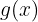 
aufstellen, für die gilt: 
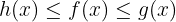und
Wenn wir diese Funktionen finden, können wir schlussfolgern, dass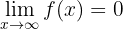 
.
Wir können beobachten, dass für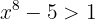 
(für hohe Werte von erfüllt). Außerdem ist für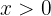 
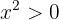. Folglich ist:
,
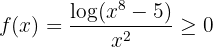wenn "groß genug" ist. Daher ist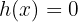 
, wobei 
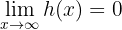ist.
Nun ermitteln wir die zweite Funktion: wir stellen fest, dass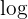 
eine wachsende Funktion ist, daher ist 
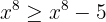, weil 
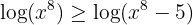ist. Wir erhalten demnach:
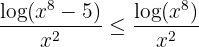
Wenn wir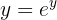 
definieren, können wir schreiben:
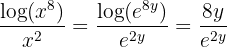
Eine sehr wichtige Eigenschaft der Exponentialfunktion ist
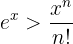
für alle Werte von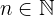 
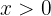und . Wenn wir 
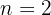betrachten, erhalten wir
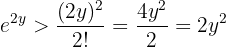
Daraus erhält man
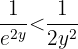
Also ist
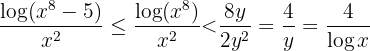
Somit is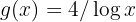t 
mit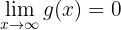 
. Außerdem ist 
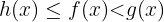. Es ist also bewiesen, dass .
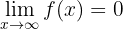Berechne den Grenzwert:
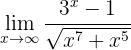
Wenn wir die Funktion gegen betrachten, erhalten wir:
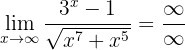
Hier können wir wieder den Grad des Zählers und Nenners betrachten, um den Grenzwert näher zu bestimmen. In diesem Fall besitzt der Zähler einen höheren Grad, daher ist
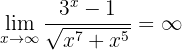
Um das zu beweisen, gehen wir wie folgt vor:
Wir müssen eine Funktion 
finden, mit der gilt , folglich:
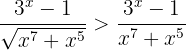
Wenn 
ist, ist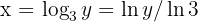 
. Daraus lässt sich schließen, dass
Wir erhalten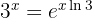 
. Gleichzeitig wissen wir, dass
,
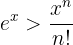wenn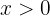 
, das heißt:
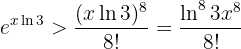
Folglich ist
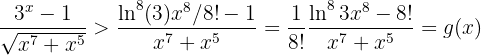
mit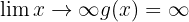 
. Der Grenzwert ist also
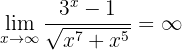
Berechne den Grenzwert:
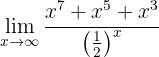
Gegen Unendlich betrachtet erhalten wir:
Der Grenzwert muss Unendlich sein, da sowohl der Zähler als auch der Nenner für einen hohen Wert von positiv ist. Um das eindeutiger sehen zu können, schreiben wir
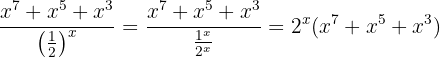
Folglich ist
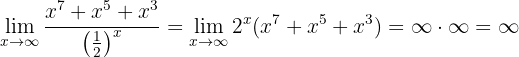
Berechne den Grenzwert:
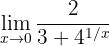
Wenn wir die Funktion gegen Null betrachten, erhalten wir:
Wir erhalten einen unbestimmten Ausdruck der Form . In diesem Fall ist 
nicht korrekt, da wir einen Grenzwert für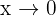 
und ein positives oder negatives nahe 0 bestimmen. (Bei Grenzwertbestimmungen mit ist das in der Regel kein Problem).
Daher müssen wir die Grenzwerte der Seiten berechnen:
1 Zuerst bestimmen wir den linksseitigen Grenzwert:
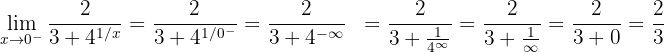
2 Nun bestimmen wir den rechtsseitigen Grenzwert:
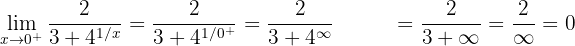
Wir stellen fest, dass die beiden seitlichen Grenzwerte unterschiedlich sind, daher gibt es keinen Grenzwert für .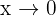
Berechne den Grenzwert:
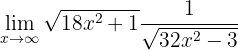
Wenn wir die Funktion gegen Unendlich betrachten, erhalten wir:
Daher müssen wir die Funktion umformen. Zuerst schreiben wir den Grenzwert in einen einzigen Bruch um:
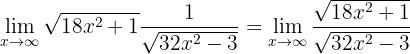
Nun teilen wir den Zähler und Nenner durch den Koeffizienten des höchsten Grades (d.h. durch , da es unter einer Wurzel steht):
Nun können wir die Funktion gegen Unendlich betrachten und erhalten:
Der Grenzwert ist daher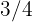 
.
Berechne den Grenzwert:
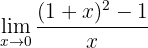
Wenn wir die Funktion gegen Null betrachten, erhalten wir:
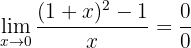
Es liegt ein unbestimmter Ausdruck vor, daher müssen wir ihn zuerst umformen. Dafür lösen wir das Binom zum Quadrat auf und erhalten:
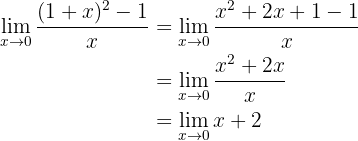
Wenn wir die Funktion jetzt gegen Null betrachten, erhalten wir:
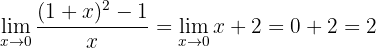
Der Grenzwert ist also 2.
Berechne den Grenzwert:
Wenn wir die Funktion gegen 3 betrachten, erhalten wir:
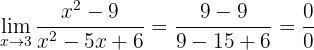
Wir erhalten wieder einen unbestimmten Ausdruck. Um ihn aufzulösen, faktorisieren wir sowohl den Zähler als auch den Nenner. Wir sehen, dass der Zähler eine Differenz aus Quadratzahlen ist; der Nenner dagegen kann faktorisiert werden, indem man Zahlen findet, die bei Multiplikation 6 und bei Addition -5 ergeben):
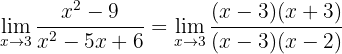
Somit können wir 
entfernen und erhalten:
Der Grenzwert ist also 6.
Berechne den Grenzwert:
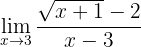
Wenn wir die Funktion gegen 3 betrachten, erhalten wir:
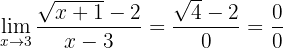
Es liegt wieder ein unbestimmter Ausdruck vor, daher müssen wir ihn zuerst umformen. Da in diesem Fall ein Ausdruck mit Radikal vorliegt, müssen wir den Bruch mit der konjugiert komplexen Zahl des Zählers multiplizieren und anschließend durch sie teilen, da sich im Zähler das Radikal befindet:
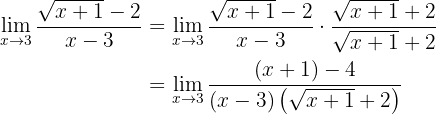
das Ergebnis ergibt sich daraus, dass "konjugierte Binome" im Zähler stehen. Wir vereinfachen weiter:
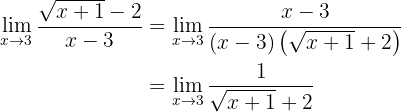
Nun können wir die Funktion gegen 3 betrachten und erhalten:
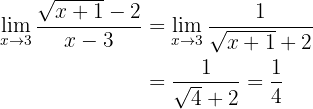
Der Grenzwert ist daher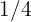 
.
Berechne den folgenden Grenzwert:
Wenn wir die Formel gegen betrachten, erhalten wir:
Es liegt ein unbestimmter Ausdruck vor. Daher müssen wir mathematisch umformen, um eine der Definition von 
ähnliche Form zu erhalten. Dafür addieren und subtrahieren wir zuerst 2 im Exponenten (den Grenzwert bezeichnen wir mit ):
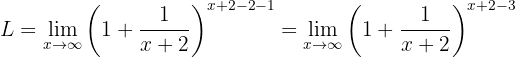
Wir formen nach den Potenzregeln um:
Wir können erkennen, dass die erste Potenz mit der Definition von für 
übereinstimmt. Der Grenzwert ist also:
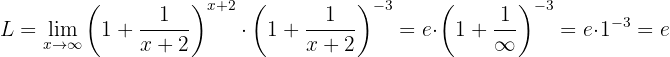
Berechne den Grenzwert:
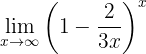
Gegen Unendlich betrachtet erhalten wir:
Daher müssen wir mathematisch umformen, um eine der Definition von ähnliche Form zu erhalten. Dafür wandeln wir zuerst den Ausdruck innerhalb der Klammer um und bezeichnen den Grenzwert mit :
Im Exponent müssen wir also auf irgendeine Weise die Form 
erhalten. Dies erreichen wir wie folgt:
Wir formen nach den Potenzregeln um:
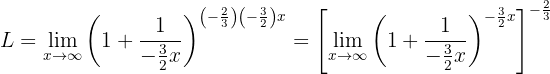
Nun können wir den Grenzwert berechnen, da wir in der äußeren Klammer ähnlich der Definition von den Ausdruck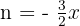 
) ausmachen können:
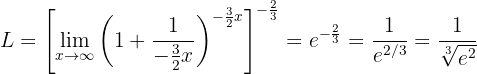
Anmerkung: die Formen 
, 
, 
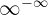und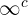 
sind für manche Werte von 
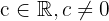keine unbestimmten Ausdrücke. Wenn wir eine dieser Formen erhalten, können wir den Grenzwert sicherer ermitteln:
Berechne den Grenzwert:
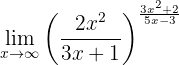
Wenn wir die Funktion gegen betrachten, sehen wir sofort, dass:
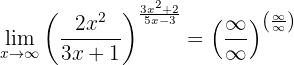
Wir vergleichen die Werte von Unendlich in den beiden Brüchen. Zuerst erkennen wir, dass
,
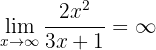da der Zähler ein Polynom höheren Grades ist (und da die Hauptkoeffizienten das gleiche Vorzeichen haben). Ähnlich verhält es sich mit
,
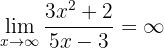aus denselben Gründen. Der Grenzwert ist also:
,
da es sich beim letzten Ausdruck um keinen unbestimmten Ausdruck handelt.
Berechne den Grenzwert:
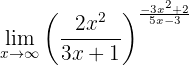
Wenn wir die Funktion wieder gegen Unendlich betrachten, erhalten wir:
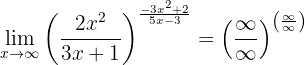
Wenn wir aber due Grenzwerte der Brüche lösen, indem wir ihren Grad der Unendlichkeit vergleichen, stellen wir fest, dass:
,
da der Zähler ein Polynom höheren Grades ist (und da die Hauptkoeffizienten das gleiche Vorzeichen haben). Außerdem ist
,
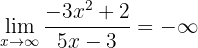da der Zähler ein Polynom höheren Grades ist, aber die Hauptkoeffizienten nicht dasselbe Vorzeichen haben. Der Grenzwert ist daher:
Berechne den Grenzwert:
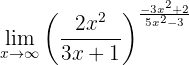
Wenn wir die Funktion gegen Unendlich betrachten, erhalten wir:
Wir betrachten die Grenzwerte der Brüche separat. Der Zähler der Basis der Potenz ist ein Polynom höheren Grades. Außerdem haben die Hauptkoeffizienten dasselbe Vorzeichen, daher ist
,
Die Polynome in den Exponenten des Zählers wie auch des Nenners haben denselben Grad. Der Grenzwert ist also der Quotient der Hauptkoeffizienten:
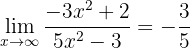
Der Grenzwert ist daher
,
da
, wenn 
.
Berechne den Grenzwert:
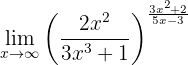
Wenn wir die Funktion gegen Unendlich betrachten, erhalten wir:
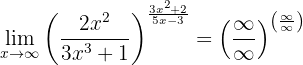
Wir betrachten die Grenzwerte der Brüche separat, um den generellen Grenzwert zu ermitteln. Wir wissen, dass
,
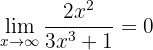da der Nenner ein Polynom höheren Grades ist. Ebenso ist
,
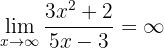da der Zähler ein Polynom höheren Grades ist und die Hauptkoeffizienten dasselbe Vorzeichen haben. Der Grenzwert ist also
,
da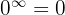 
(d.h. kein unbestimmter Ausdruck ist).
Berechne den Grenzwert:
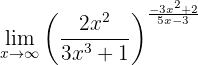
Dieser Grenzwert ist praktisch derselbe wie der vorherige, bis auf ein verändertes Vorzeichen:
Wir betrachten die Grenzwerte der Brüche separat, um den generellen Grenzwert zu ermitteln. Wie im vorherigen Beispiel erhalten wir
,
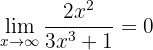da der Nenner ein Polynom höheren Grades ist. Ebenso ist
,
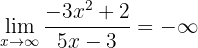da der Zähler ein Polynom höheren Grades ist und die Hauptkoeffizienten unterschiedliche Vorzeichen haben. Der Grenzwert ist also
Hierbei handelt es sich um einen unbestimmten Ausdruck. Wir müssen also die Regel hierfür anwenden:
und erhalten
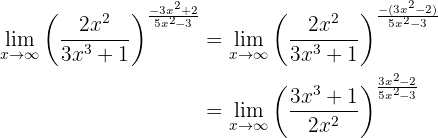
Folglich ist
Wir erhalten
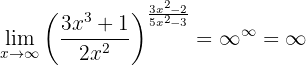
Anmerkung: es ist wichtig, diese Schreibweise anzuwenden. 
ist nämlich ein unbestimmter Ausdruck (d.h. wir können verschiedene Funktionen bilden, in denen dieser unbestimmte Ausdruck einen anderen Wert annimmt).
Berechne den Grenzwert:
Wenn wir die Funktion wie im vorherigen Beispiel gegen Unendlich betrachten, erhalten wir:
Wie vorher betrachten wir die Funktion gegen Unendlich und erhalten:
,
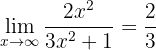da die Polynome im Zähler und Nenner denselben Grad aufweisen. Der Grenzwert ist also der Quotient der Hauptkoeffizienten. Ebenso ist
D.h. der Grenzwert ist
Berechne den Grenzwert:
Gegen Unendlich betrachtet erhalten wir:
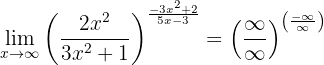
Wir betrachten die Grenzwerte der Brüche separat:
,
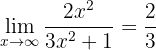da die Polynome im Zähler und Nenner denselben Grad aufweisen. Der Grenzwert ist also der Quotient der Hauptkoeffizienten. Ebenso ist
,
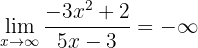da der Zähler ein Polynom höheren Grades ist und die Hauptkoeffizienten unterschiedliche Vorzeichen haben. Der Grenzwert ist also
,
da wir einen Ausdruck der Form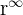 
mit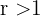 
erhalten.
Berechne den Grenzwert:
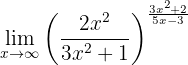
Gegen Unendlich betrachtet erhalten wir:
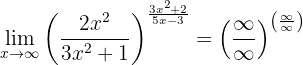
Dieser Grenzwert ist praktisch derselbe wie der vorherige, bis auf ein verändertes Vorzeichen. Wir betrachten die Grenzwerte der Brüche separat:
,
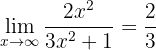da die Polynome im Zähler und Nenner denselben Grad aufweisen. Der Grenzwert ist also der Quotient der Hauptkoeffizienten. Ebenso ist
,
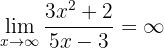da der Zähler ein Polynom höheren Grades ist und die Hauptkoeffizienten dieselben Vorzeichen haben. Der Grenzwert ist also
,
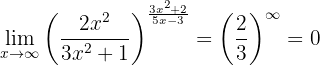da wir einen Ausdruck der Form 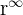mit 
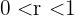erhalten.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
