Wähle die Option, die die Zielmenge jeder der Funktionen angibt, denen diese Grafiken entsprechen:
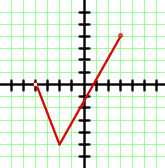
Bitte wähle eine Antwort aus.
Aus der Grafik geht hervor, dass der minimale Wert, den die Funktion auf der y-Achse erreicht,  ist und der maximale Wert
ist und der maximale Wert  ist. Somit ist die Lösung der Zielmenge der Funktion das Intervall
ist. Somit ist die Lösung der Zielmenge der Funktion das Intervall 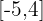 .
.
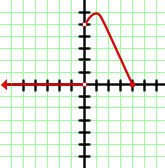
Bitte wähle eine Antwort aus.
Aus der Grafik geht hervor, dass der minimale Wert, den die Funktion auf der y-Achse erreicht,  ist und der maximale Wert
ist und der maximale Wert  ist. Somit ist die Lösung der Zielmenge der Funktion das Intervall
ist. Somit ist die Lösung der Zielmenge der Funktion das Intervall 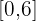 .
.
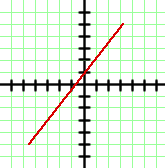
Bitte wähle eine Antwort aus.
Der Graph entspricht einer Geraden, die von  bis
bis 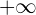 stetig ist. Das heißt, dass die Lösung der Zielmenge des Graphen das Intervall
stetig ist. Das heißt, dass die Lösung der Zielmenge des Graphen das Intervall 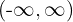 ist, was äquivalent zu
ist, was äquivalent zu  ist.
ist.
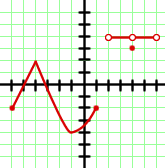
Bitte wähle eine Antwort aus.
Aus der Grafik geht hervor, dass der minimale Wert, den die Funktion auf der Achse  erreicht,
erreicht,  ist und der maximale Wert
ist und der maximale Wert  . Auperdem Außerdem haben wir zwei zusätzliche Punkte, an denen es einen Graphen gibt. Daher ist die Lösung der Zielmenge die Vereinigung des Intervalls plus zwei Punkte. Das heißt,
. Auperdem Außerdem haben wir zwei zusätzliche Punkte, an denen es einen Graphen gibt. Daher ist die Lösung der Zielmenge die Vereinigung des Intervalls plus zwei Punkte. Das heißt,  .
.
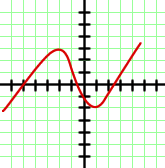
Bitte wähle eine Antwort aus.
Wenn wir uns den Graphen ansehen, können wir erkennen, dass er stetig ist und sowohl für  als auch für
als auch für 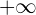 weiter steigt. Somit ist die Lösung der Zielmenge des Graphen das Intervall
weiter steigt. Somit ist die Lösung der Zielmenge des Graphen das Intervall 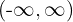 .
.
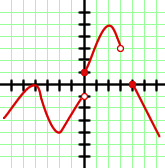
Bitte wähle eine Antwort aus.
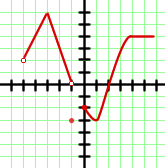
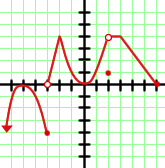
Dieser Graph entspricht einer abschnittsweise definierten Funktion. Wir stellen fest, dass die unteren Extremwerte bis  weiter steigen und das Maximum im Punkt
weiter steigen und das Maximum im Punkt  liegt. Außerdem haben wir einen Abschnitt des Graphen, der zum Intervall
liegt. Außerdem haben wir einen Abschnitt des Graphen, der zum Intervall  gehört. Daher ist die Lösung der Zielmenge der Funktion die Vereinigung der Intervalle:
gehört. Daher ist die Lösung der Zielmenge der Funktion die Vereinigung der Intervalle: 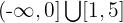 .
.
Bitte wähle eine Antwort aus.
Der Graph entspricht einer abschnittsweise definierten Funktion mit der Lösung 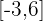 für die Zielmenge der Funktion.
für die Zielmenge der Funktion.
Bitte wähle eine Antwort aus.
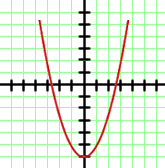
Der Graph entspricht einer quadratischen Funktion mit dem Tiefpunkt 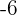 , die kein Maximum hat, da die Funktion bis
, die kein Maximum hat, da die Funktion bis 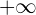 steigt. Somit ist die Lösung der Zielmenge der Funktion
steigt. Somit ist die Lösung der Zielmenge der Funktion  .
.
Bitte wähle eine Antwort aus.
Der Graph entspricht einer abschnittsweise definierten Funktion mit den Tief- und Hochpunkten  und
und  . Somit lautet die Lösung der Zielmenge des Graphen
. Somit lautet die Lösung der Zielmenge des Graphen  .
.
Bitte wähle eine Antwort aus.
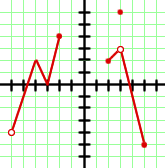
Der Graph entspricht einer abschnittsweise definierten Funktion. Wir stellen fest, dass die Zielmenge der Funtion das Intervall 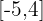 plus dem Punkt
plus dem Punkt  ist. Die Lösung ist also
ist. Die Lösung ist also  .
.
Mit KI zusammenfassen:


