Kapitel
Eine Kegelfläche entsteht durch die Drehung einer Geraden 
, die Mantellinie genannt wird, um eine andere Gerade 
, die Achse, die sie in einem Punkt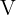 
, dem Scheitelpunkt, schneidet.
- = die Mantellinie
- = die Achse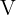
- = der Scheitelpunkt
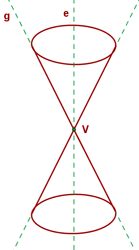
Elemente eines Kegels
- Fläche - eine kegelförmige Rotationsfläche entsteht durch die Drehung einer Geraden um eine andere feste Gerade, die sogenannte Achse, die sie schräg halbiert.
- Mantellinie - die Mantellinie ist eine der schrägen Geraden.
- Schnittpunkt - der Schnittpunkt ist der zentrale Punkt, in dem sich die Mantellinien schneiden.
- Hojas - las hojas son las dos partes en las que el vértice divide a la superficie cónica de revolución.
- Schnitte - die Schnittkurve eines Kegels mit einer Ebene, die nicht durch seinen Scheitelpunkt verläuft, wird als Kegelschnitt bezeichnet. Je nach dem Verhältnis zwischen dem Kegelwinkel
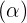und der Neigung der Ebene in Bezug auf die Kegelachse 
können verschiedene Kegelschnitte erhalten werden.
Ellipse
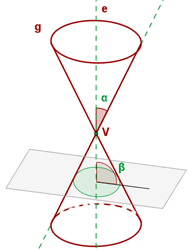
Die Ellipse ist der Schnitt, der auf einer kegelförmigen Rotationsfläche durch eine zur Achse schiefe Ebene entsteht, die nicht parallel zur Mantellinie verläuft und mit dieser einen Winkel bildet, der größer ist als der Winkel, den die Achse und die Mantellinie bilden.
Die Ellipse ist eine geschlossene Kurve.
Kreis
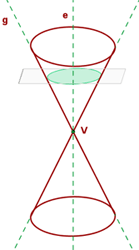
Der Kreis ist der Schnitt, der durch eine Ebene senkrecht zur Achse entsteht.
Der Kreis ist ein Sonderfall der Ellipse.
Parabel
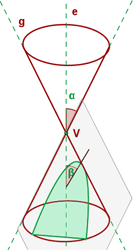
Die Parabel entsteht beim Schnitt eines geraden Kreiskegels mit einer Ebene, die parallel zu einer Mantellinie verläuft.
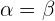
Die Parabel ist eine geöffnete Kurve und verläuft ins Unendliche.
Hyperbel
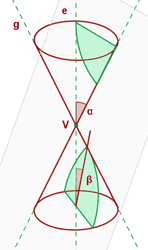
Die Hyperbel entsteht beim Schnitt einer Ebene mit einem geraden Kreiskegel.
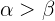
Die Hyperbel ist eine geöffnete Kurve, die sich ins Unendliche erstreckt und aus zwei separaten Ästen besteht.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
