Das Konzept der Funktion ist sowohl in der Mathematik als auch in der Physik, Chemie, Medizin, Statistik, Wirtschaft, Ingenieurwesen, Psychologie und anderen Bereichen von großer Bedeutung. Und wahrscheinlich hast du dich schon einmal gefragt, welche Beispiele für Funktionen es im Alltag gibt.
Wenn wir über Beispiele für Funktionen im Alltag nachdenken, fällt uns ein Verkaufsautomat ein, da man einen Code eingibt und die Maschine einem ein Produkt ausgibt. Auch das Telefonieren ist ein Beispiel für eine Funktion: Man gibt eine Nummer ein und wird mit dem anderen Gerät verbunden.
Es gibt noch viele weitere Beispiele wie diese, die du in deinem Alltag finden kannst, wenn du das Konzept der Funktion anwendest, das wir dir im Folgenden vorstellen.
Konzept der Funktion
Eine Funktion ist eine Beziehung zwischen zwei Größen, sodass jedem Wert der ersten Größe (bekannt als Definitionsmenge) ein einziger Wert der zweiten Größe (bekannt als Abbildung) entspricht.
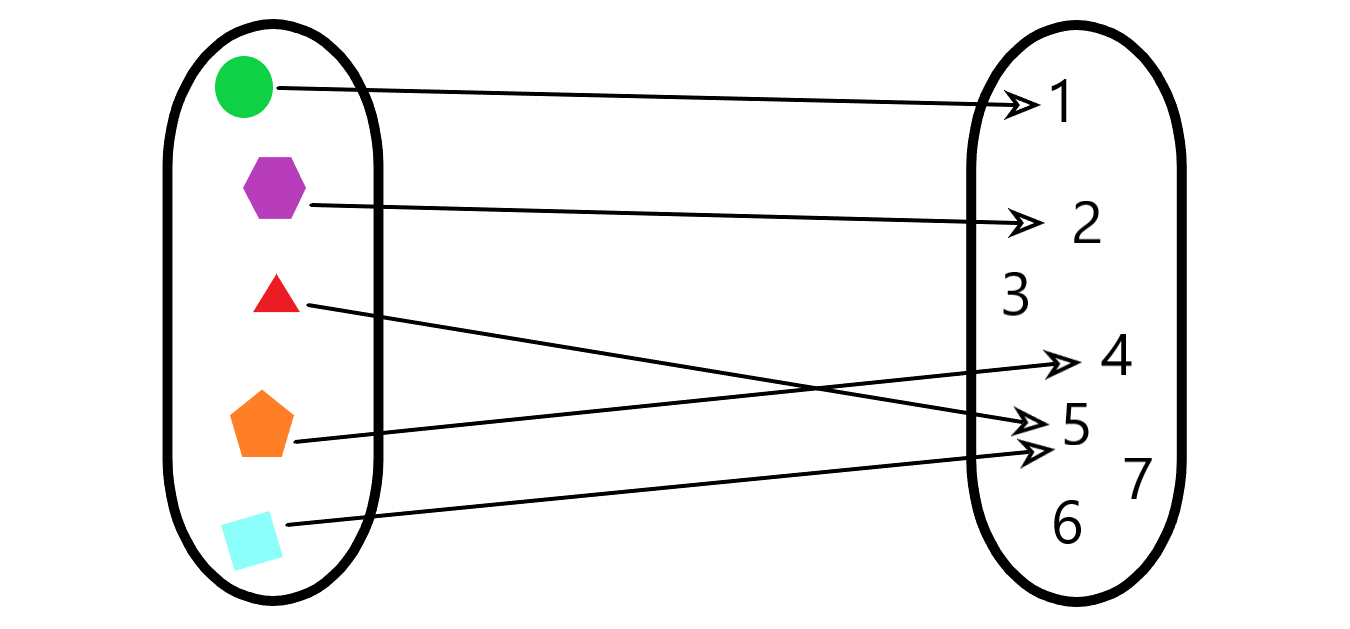
Beispiele für Funktionen
1Ein gängiges Beispiel für eine numerische Funktion ist das Verhältnis zwischen Position und Zeit bei der Bewegung eines Körpers.
Nehmen wir an, dass ein Auto mit einer Beschleunigung von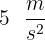 
eine Strecke 
zurücklegt, die von der vergangenen Zeit 
abhängt.
Die mathematische Funktion, die die Strecke 
beschreibt, die das Auto in der Zeit zurücklegt, wird durch folgenden Ausdruck angegeben: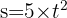 
Wir können eine Tabelle mit den Werten der Variablen erstellen, indem wir die zurückgelegte Strecke zu einem bestimmten Zeitpunkt für verschiedene Zeitpunkte notieren:
| t | 0,447 | 0,632 | 0,774 | 0,894 |
|---|---|---|---|---|
| s=5 t² | 1 | 2 | 3 | 4 |
Ebenso können wir die Position des Autos grafisch wie folgt darstellen:
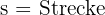
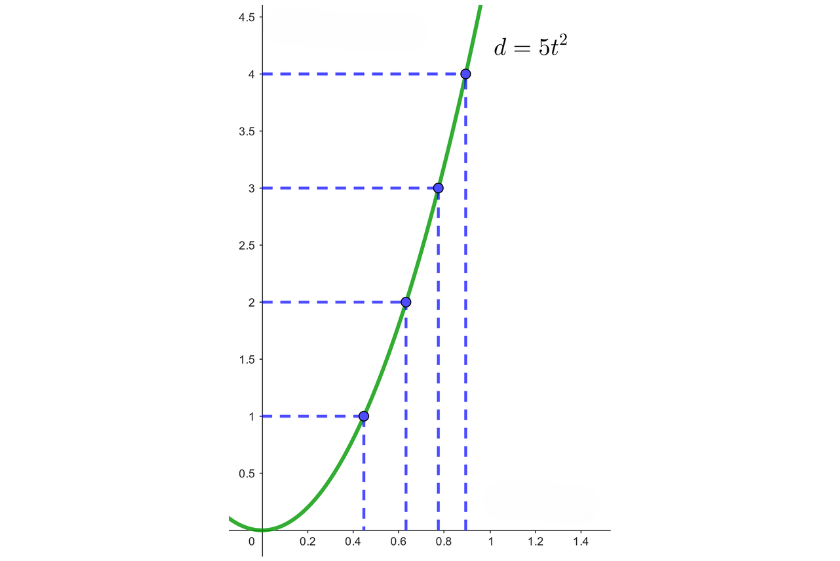
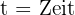
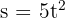
In diesen Fällen wird gesagt, dass die abhängige Variable ist (da sie vom Wert von abhängt) und die unabhängige Variable.
2Taxifahrt.
Nehmen wir an, dass der Preis für eine Taxifahrt wie folgt gegeben ist:
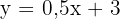
Wobei 
den Endpreis (abhängige Variable) darstellt, 
die Entfernung in km, die die Fahrt dauert (unabhängige Variable), und 
dem Wert entspricht, der festgelegt wurde, um sicherzustellen, dass eine geringe Kilometerzahl für den Fahrer rentabel ist.
Wir können eine Tabelle mit den Werten der Variablen erstellen, indem wir den Preis der Fahrt für eine bestimmte Strecke für verschiedene Strecken angeben:
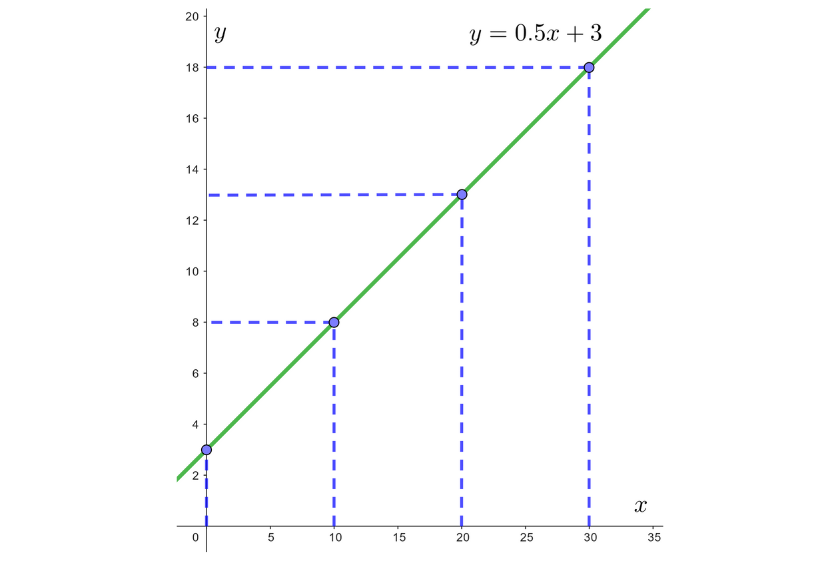
| x | 0 | 10 | 20 | 30 |
|---|---|---|---|---|
| y=0,5x+3 | 3 | 8 | 13 | 18 |
Ebenso können wir die Position des Autos grafisch wie folgt darstellen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
