Eine kurze Erläuterung der Funktionen
Im täglichen Leben gibt es viele Dinge, die miteinander in Beziehung stehen, z. B. die Größe eines Hauses mit seinem Preis, das Alter einer Person mit ihrer körperlichen Verfassung, der Verkehr in einer Stadt und die Anzahl der Autos in ihr, sogar der Preis eines Taxidienstes und die Nachfrage, die in diesem Moment besteht (Uber). Dies sind Beispiele für „Funktionen“, die jeden Tag vorhanden sind, ohne dass wir uns dessen bewusst sind.
Informell könnten wir eine Funktion als eine Maschine betrachten, der wir ein Objekt geben und die uns ein anderes Objekt zuwirft, so als wäre sie ein Automat für Süßigkeiten – wir werfen Geld ein, wählen das Produkt aus und sie gibt es uns aus.
Dies gibt uns eine Vorstellung davon, was eine Funktion sein könnte: Eine Art Maschine, die Objekte miteinander in Beziehung setzt – aber welche Objekte? Die, die wir ihr geben, mit denen, die wir zurückbekommen. Formal gesehen muss das Konzept einer Funktion jedoch bestimmte Einschränkungen (Eigenschaften) erfüllen. Eine davon ist beispielsweise, dass die Funktion jedes Mal, wenn wir ihr ein Objekt geben, nur ein einziges Objekt zurückgeben darf. Es wäre sehr seltsam, eine Münze einzuwerfen, wenn wir Schokolade aus einem Automaten möchten und er uns Schokolade, ein paar Kekse und dann noch ein Getränk dazu gibt, nicht wahr?
Definition von Beziehung und Funktion
Um formell zu definieren, was eine Funktion ist, müssen wir zunächst eine Beziehung zwischen Mengen definieren.
Bei zwei Mengen 
und 
nennen wir die Beziehung von 
in 
jede Übereinstimmung zwischen einigen der Elemente von mit den Elementen von 
.
Beispiele
1. Wir sehen uns die Mengen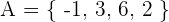 
und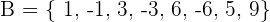 
an. Die Beziehung ist durch folgende Abbildung gegeben
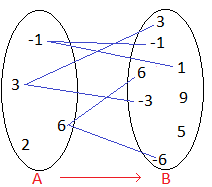
Dabei ist zu beachten, dass nicht alle Elemente von mit Elementen von in Beziehung stehen, z. B. hat das Element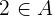 
keine Abbildung in .
Hinweis. Bei einer Mengenbeziehung ist es nicht notwendig, dass alle Elemente der beiden Mengen miteinander in Beziehung stehen.
Wir können die Beziehung auch als eine Menge schreiben, in diesem Fall wäre die Beziehung durch die Menge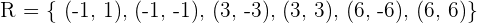 
gegeben. Es ist zu beachten, dass für jedes geordnete Paar der erste Eintrag, von links nach rechts gezählt, ein Element von 
ist, während der zweite Eintrag das Element von ist, zu dem es in Beziehung steht.
2. Wir sehen uns die Mengen 
und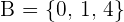 
an. Die Beziehung ist durch folgende Abbildung gegeben
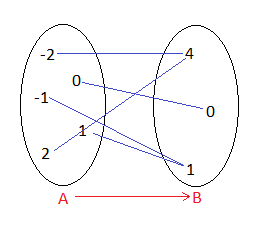
In diesem Fall stehen alle Elemente von in Beziehung zu Elementen von .
Diese Beziehung in Form einer Menge wäre gegeben durch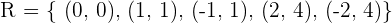 
.
Da wir nun wissen, was eine Beziehung ist, können wir eine Funktion zwischen Mengen definieren.
Gegeben sind zwei Mengen und . Eine Funktion von in ist eine Beziehung, die folgende Eigenschaften erfüllt:
- Jedes Element der Menge muss mit einem Element der Menge in Beziehung stehen.
- Kein Element der Menge darf mit mehr als einem Element der Menge in Beziehung stehen.
Diese beiden Eigenschaften lassen sich dahingehend reduzieren, dass jedes Element der Menge mit einem einzigen Element der Menge in Beziehung stehen muss.
Bei einer Funktion einer Menge in einer Menge wird die Menge als Definitionsmenge bezeichnet, während die Menge als Zielmenge bezeichnet wird.
Normalerweise wird eine Funktion mit 
angegeben, und um auszudrücken, dass sie von einer Menge in eine Menge übergeht, schreibt man
.
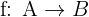Außerdem: Wenn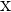 
ein Element in ist, wird das Element, mit dem es in in Beziehung steht, wie folgt angegeben:
,
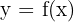Dies kann als 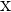interpretiert werden, das sich auf 
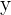nach den Regeln von bezieht.
Wenn wir die Schreibweise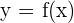 
verwenden, ist 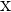die unabhängige Variable und 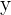die abhängige Variable.
Beispiele
1. Beispiel 1 der Beziehungen ist keine Funktion, da es Elemente der Definitionsmenge, , gibt, die mit keinem Element der Zielmenge, , in Beziehung stehen. Darüber hinaus gibt es Elemente in , die mit mehr als einem Element in in Beziehung stehen.
2. Beispiel 2 der Beziehungen ist eine Funktion, da alle Elemente der Defintionsmenge, , mit einem einzigen Element der Zielmenge, , in Beziehung stehen. In diesem Fall lässt sich nämlich feststellen, dass für alle 
die Beziehung zu den Elementen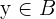 
durch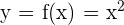 
gegeben ist.
3. Wir sehen uns die Menge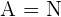 
, die Menge 
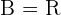sowie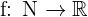 
gegeben durch 
an. Handelt es sich um eine Funktion? Nun, das kommt darauf an. Mal sehen, warum.
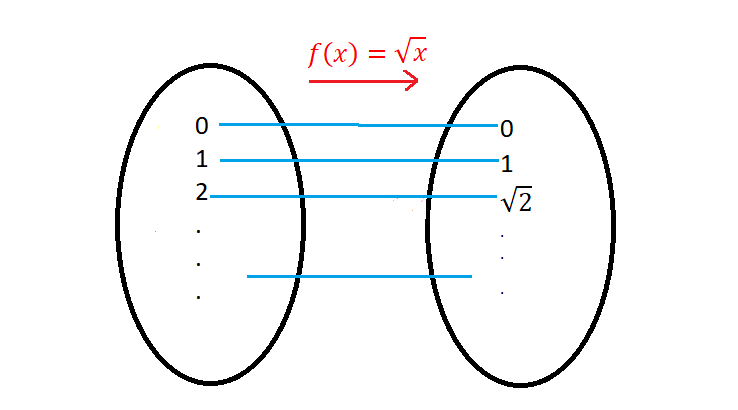
- Zunächst ist zu beachten, dass für jede beliebige Zahl, z. B.
, gilt: 
, da 
. Daher würden wir in diesem Fall jedem Element der Definitionsmenge zwei Elemente der Zielmenge zuordnen, und es wäre keine Funktion. - Wenn wir jedoch von der Wurzel einer Zahl sprechen, betrachten wir in der Regel nur den positiven Teil. Wenn also nichts anderes angegeben ist, gilt für jede Zahl, z. B. ,
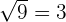. Somit wäre 
tatsächlich eine Funktion, da wir eine eindeutige Entsprechung für jedes Element in der Definitionsmenge haben. Außerdem haben wir am Anfang festgelegt, dass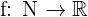 
und betrachten somit die gesamte Definitionsmenge 
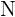. - Wenn wir nur den negativen Teil der Wurzel betrachten möchten, müssen wir
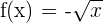definieren. In diesem Fall hätten wir, wie im vorherigen, ebenfalls eine Funktion.
Wenn eine Funktion erfüllt, dass sowohl ihre Definitionsmenge als auch ihre Zielmenge Teilmengen der reellen Zahlen sind (
), dann handelt es sich um eine reelle Funktion.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
