Der Kreis und seine Gleichung
Der Kreis ist definiert als die Menge der Punkte in der Ebene, die von einem festen Punkt
, den wir Mittelpunkt nennen, gleich weit entfernt sind.
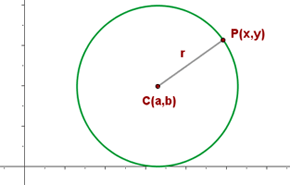
Deshalb erfüllt jeder Punkt 
des Kreises
Die Entfernung 
heißt Radius. Somit gilt Folgendes:
Wir quadrieren die vorhergehende Gleichung und erhalten:
Die vorherige Gleichung wird allgemeine Kreisgleichung genannt. Um diese Gleichung zu erhalten, müssen wir die Binome zum Quadrat auflösen:
Wir stellen die Gleichung wie folgt um:
Wir substituieren wie folgt:
Daher kann die Kreisgleichung in der folgenden Form geschrieben werden:
Auch diese Gleichung ist eine Form der Kreisgleichung. Der Mittelpunkt ist gegeben durch:
Für den Radius gilt:
Hierbei ist zu beachten, dass die Gleichung
Folgendes erfüllen muss, damit sie einen Kreis beschreibt:
1 Die folgende Ungleichheit muss erfüllt sein
2 Es gibt keinen Term 
(das heißt, 
und 
werden nicht multipliziert).
3 
und 
haben den Koeffizienten 1.
Anmerkung: Falls und einen anderen Koeffizienten als 1 haben, müssen beide denselben Koeffizienten haben. So können wir die Gleichung durch diesen Koeffizienten teilen, um die allgemeine Kreisgleichung zu erhalten.
Anmerkung: Falls der Mittelpunkt im Koordinatenursprung liegt, sieht die Kreisgleichung wie folgt aus
Übungsaufgaben zur Kreisgleichung
Bestimme die Gleichung eines Kreises mit dem Mittelpunkt bei 
und dem Radius 2.
Die allgemeine Kreisgleichung lautet:
Durch die Auflösung der Binome erhalten wir folgende Form der Kreisgleichung:
Durch Zusammenfassen der Konstanten erhalten wir
Gegeben ist der Kreis mit der Gleichung 
. Bestimme seinen Mittelpunkt und Radius.
Der Mittelpunkt ist gegeben durch
Für den Radius gilt:
Daher ist der Radius 
.
Bestimme die Gleichung eines Kreises, der durch die Punkte 
, 
und 
verläuft.
Um einen Kreis zu bestimmen, der durch drei Punkte verläuft, müssen wir immer die folgende Form der Kreisgleichung anwenden. Dies erleichtert uns die Arbeit.
Wir ersetzen die Werte für und in der Gleichung:
Indem wir ersetzen, (das heißt, 
und 
), erhalten wir 
. Somit gilt:
Dies gilt auch für . Wir erhalten 
; für erhalten wir 
. Daher ergibt sich folgendes Gleichungssystem:
Wir lösen das System (am einfachsten geht es, indem wir die dritte Gleichung von der zweiten Gleichung subtrahieren). Schließlich erhalten wir:
Somit lautet die allgemeine Kreisgleichung
Gib an, ob die Gleichung 
einen Kreis beschreibt. Wenn ja, bestimme Mittelpunkt und Radius.
1 Wir stellen fest, dass die Koeffizienten von und gleich sind (allerding nicht 1). Deshalb dividieren wir die Gleichung durch 4:
2 Außerdem gibt es keinen Term .
3 Abschließend prüfen wir, ob die Ungleichheit mit den Termen 
, 
und 
erfüllt ist:
Da alle drei Bedingungen erfüllt sind, beschreibt die Gleichung also tatsächlich einen Kreis.
Wir ermitteln den Mittelpunkt:
Für den Radius gilt:
Der Radius ist 
.
Bestimme die Gleichung eines Kreises, dessen Mittelpunkt der Punkt 
ist und der die x-Achse tangiert.
Hier müssen wir einen Kreis finden, der eine Gerade tangiert. In solch einem Fall ist der Radius immer die Entfernung zwischen dem Punkt und der Geraden (diese soll unser Kreis tangieren). Daher müssen wir die Entfernung zwischen dem Punkt und der Geraden bestimmen.
Als Erstes erinnern wir uns daran, dass die x-Achse die Gerade ist. Die Entfernung von einem Punkt 
zu einer Geraden 
ist durch folgende Formel gegeben:
Daher ist die Entfernung zwischen und der Geraden 
Die allgemeine Kreisgleichung lautet:
Folgende Grafik zeigt die Abbildung:
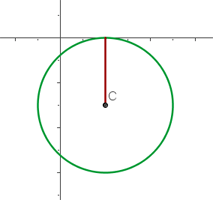
Bestimme die Gleichung eines Kreises, dessen Mittelpunkt im Punkt 
liegt und der die y-Achse tangiert.
Ähnlich wie in der vorhergehenden Aufgabe müssen wir die Entfernung vom Punkt bis zur y-Achse bestimmen. Die y-Achse ist durch die Gleichung $s \equiv x = 0$ gegeben. Somit ist die Entfernung:
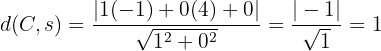
Die Kreisgleichung lautet also
Folgende Grafik zeigt die Abbildung:
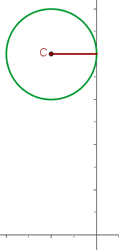
Bestimme die Gleichung eines Kreises, dessen Mittelpunkt der Schnittpunkt der Geraden 
$ und 
ist und dessen Radius 5 ist.
Um die Gleichung zu bestimmen, müssen wir nur den Punkt finden, in dem sich die zwei Geraden schneiden (den Radius haben wir bereits). Dazu setzen wir die Gleichungen gleich:
Wir erhalten 
; das heißt 
. Indem wir in eine der Gleichungen einsetzen, erhalten wir 
. Der Mittelpunkt ist also der Punkt 
und die Kreisgleichung lautet
oder, in der anderen Form
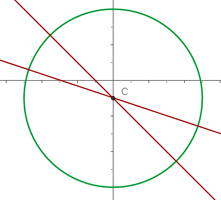
Folgende Grafik zeigt die Abbildung:
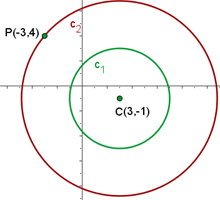
Bestimme die Gleichung eines Kreises, der durch den Punkt 
verläuft und der konzentrisch zum Kreis 
ist.
Zur Lösung dieses Problems haben wir zwei Möglichkeiten:
Am einfachsten ist es, wenn wir daran denken, dass alle Kreise, die konzentrisch zu sind, folgende Gleichung haben:
Daher ersetzen wir den Punkt , um den Wert für zu bestimmen:
Das heißt, 
. Deshalb gilt 
. Die Gleichung des Kreises lautet also
Anmerkung: Die andere Möglichkeit liegt darin, den Mittelpunkt von zu bestimmen und die allgemeine Kreisgleichung zu nutzen, um den Radius bestimmen zu können.
Folgende Grafik zeigt die Abbildung:
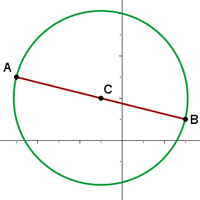
Die äußersten Punkte eines Kreises sind die Punkte 
und 
. Wie lautet die Gleichung dieses Kreises?
Um dieses Problem zu lösen, müssen wir den Radius und den Mittelpunkt bestimmen.
Der Radius ist die Hälfte des Durchmessers und somit die Hälfte der Entfernung zwischen und :
Außerdem liegt der Mittelpunkt in der Mitte von und :
Somit lautet die allgemeine Gleichung des Kreises:
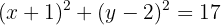
Die andere Form der Kreisgleichung lautet:
Folgende Grafik zeigt die Abbildung:
Bestimme die Gleichung eines Kreises, der konzentrisch zum Kreis 
ist und der die Gerade 
tangiert.
Um diese Gleichung zu lösen, müssen wir den Mittelpunkt des Kreises ermitteln. Wir nutzen also die allgemeine Kreisgleichung. Der Mittelpunkt ist gegeben durch:
Sobald wir den Mittelpunkt bestimmt haben, müssen wir die Entfernung vom Mittelpunkt zur gegebenen Geraden ermitteln. Diese Entfernung ist dann der Radius:
Die Gleichung des Kreises lautet also:
Folgende Grafik zeigt die Abbildung:
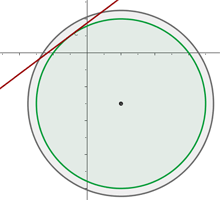
Bestimme die Gleichung des Kreises, der durch die Punkte 
und 
verläuft und dessen Mittelpunkt auf der Geraden 
liegt.
Da wir zur Lösung den Mittelpunkt benötigen, nutzen wir die allgemeine Kreisgleichung (nicht die andere Form der allgemeinen Kreisgleichung). Wenn der Mittelpunkt des Kreises ist und sein Radius, wissen wir, dass der Mittelpunkt Folgendes erfüllt
Die Gleichung des Kreises lautet dagegen
Wenn wir den Punkt ersetzen, erhalten wir
Dies gilt auch für den Punkt und wir erhalten:
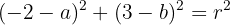
Auf diese Weise erhalten wir folgende Gleichungssysteme (nichtlinear):
Um zu lösen, setzen wir die ersten beiden Gleichungen gleich (da für beide 
gilt):
Wenn wir die Binome auflösen und entsprechende Terme streichen, erhalten wir:
Mit der dritten Gleichung bestimmen wir 
, um 
zu erhalten. Wenn wir in die vorhergehende Gleichung einsetzen, erhalten wir
Daraus folgt, dass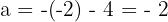 
. Schließlich ersetzen wir und 
in der ersten Gleichung des Gleichungssystems und erhaltenen 
. Die allgemeine Kreisgleichung lautet also
Folgende Grafik zeigt die Abbildung:
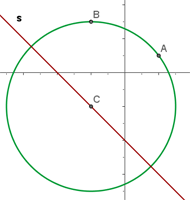
Bestimme die Gleichung des Kreises, der durch den Punkt 
verläuft, dessen Radius 
ist und dessen Mittelpunkt sich auf der Winkelhalbierenden des ersten und dritten Quadranten befindet.
Zunächst müssen wir beachten, dass die Winkelhalbierende des ersten und dritten Quadranten die Gerade 
oder 
ist. Das heißt, für den Mittelpunkt muss gelten, dass 
. Deshalb schreiben wir den Mittelpunkt in der Form 
.
Wir wissen, dass er durch den Punkt verläuft und sein Radius 
ist. Wir ersetzen in der allgemeinen Form der Kreisgleichung und erhalten
Wir haben nur die Unbekannte und können so die Binome auflösen:
Wir haben also eine quadratische Gleichung. Indem wir die allgemeine Formel (oder eine andere Methode) anwenden, erhalten wir als Ergebnis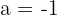 
und 
.
Es gibt also zwei Kreise, die die Bedingungen des Problems erfüllen. Der Mittelpunkt des Ersten ist 
. Deshalb lautet seine Gleichung:
Der Mittelpunkt des zweiten Kreises ist 
und seine Gleichung lautet:
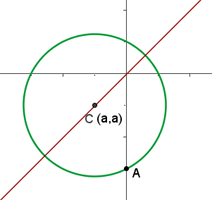
Folgende Grafik zeigt die Abbildung:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
