Kapitel

Definition des Logarithmus
Der Logarithmus einer Zahl zu einer bestimmten Basis ist der Exponent, auf den die Basis erhöht werden muss, um diese Zahl zu erhalten.
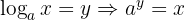
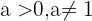
Wobei  die Basis,
die Basis,  die Zahl und
die Zahl und  der Logarithmus ist.
der Logarithmus ist.
Dezimallogarithmen und natürliche Logarithmen
Dezimallogarithmen haben die Basis  . Sie werden durch
. Sie werden durch 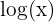 dargestellt.
dargestellt.
Natürliche Logarithmen haben  . Sie werden durch
. Sie werden durch 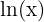 o
o  dargestellt.
dargestellt.
Beispiele für die Anwendung der Definition des Logarithmus
Schreibe die folgenden Logarithmen in Exponentialschreibweise
1 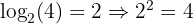
2 
3 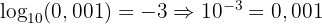
4 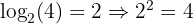
Berechne anhand der Definition des Logarithmus und der Algebra den Wert der Unbekannten in den folgenden Gleichungen
1 
Wende die Definition des Logarithmus an und wandle die  in einen Dezimalbruch um und vereinfache ihn:
in einen Dezimalbruch um und vereinfache ihn:
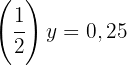
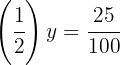

Die  wird in Potenzform gebracht und die Exponenten werden gleichgesetzt
wird in Potenzform gebracht und die Exponenten werden gleichgesetzt
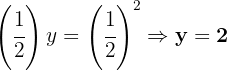
2 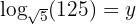
Wende die Definition des Logarithmus an, und die Wurzel wird in Form einer Potenz des gebrochenen Exponenten dargestellt
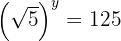
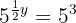
Gleiche die Exponenten an
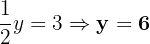
3 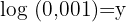
Wende die Definition des Logarithmus an und 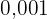 wird in einen Dezimalbruch umgewandelt
wird in einen Dezimalbruch umgewandelt

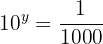
Wandle den Quotienten in eine Potenz zur Basis  um und gleiche die Exponenten an
um und gleiche die Exponenten an
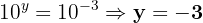
4 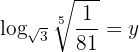
Wende die Definition des Logarithmus an, die Wurzeln werden in die Form einer Potenz des gebrochenen Exponenten gebracht und die Exponenten werden gleichgesetzt
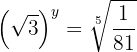


5 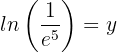
Wende die Definition des Logarithmus an, wobei Du berücksichtigst, dass die Basis des natürlichen Logarithmus  ist.
ist.
Der Bruch wird in die Potenzform gebracht und die Exponenten werden ausgeglichen

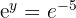
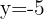
Eigenschaften von Logarithmen
1 Der Logarithmus eines Produkts ist gleich der Summe der Logarithmen der Faktoren
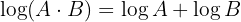

2 Der Logarithmus eines Quotienten ist gleich der Differenz aus dem Logarithmus des Dividenden und dem Logarithmus des Divisors
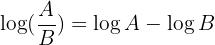
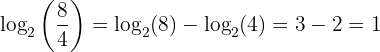
3 Der Logarithmus einer Potenz ist gleich dem Produkt aus dem Exponenten und dem Logarithmus der Basis
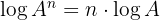

4 Der Logarithmus einer Wurzel ist gleich dem Quotienten aus dem Logarithmus des Radikanden und dem Wurzelindex
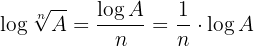
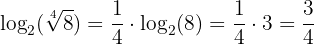
Aus den Eigenschaften  und
und  kannst Du ableiten, dass:
kannst Du ableiten, dass:

5 Der Basislogarithmus ' ' de '
' de ' ' ist
' ist  .
.
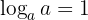
6 Der Logarithmus von  ist
ist  (unabhängig von der Basis des Logarithmus)
(unabhängig von der Basis des Logarithmus)
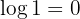
Deshalb:
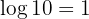
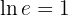
7 Das Argument eines Logarithmus muss immer größer als Null sein
Für  ist erfüllt, dass
ist erfüllt, dass 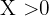
Logarithmusfunktion
Die Logarithmusfunktion zur Basis  ist die Umkehrung der Exponentialfunktion zur Basis
ist die Umkehrung der Exponentialfunktion zur Basis  .
.
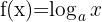
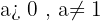
Beispiele für Logarithmusfunktionen

 | 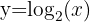 |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
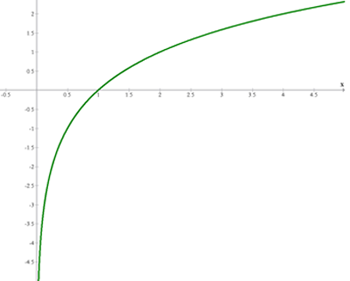
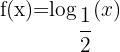
 |  |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
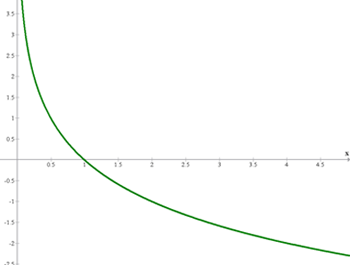
Die Eigenschaften von Logarithmusfunktionen
- Bereich:
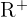
- Route:

- Sie ist kontinuierlich
- Die Punkte
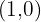 und
und 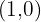 gehören zum Graphen.
gehören zum Graphen. - Er ist injektiv (kein Bild hat mehr als ein Original).
- Steigend, wenn
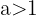
- Abnehmend, wenn
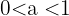
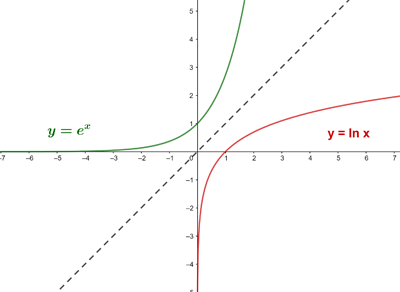
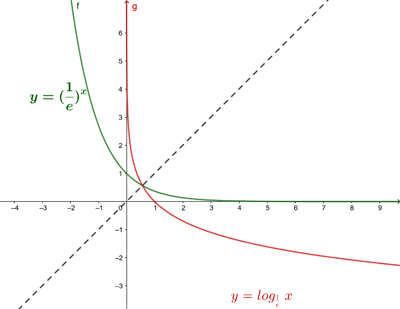
Der Graph der Logarithmusfunktion ist symmetrisch (in Bezug auf die Winkelhalbierende des ersten und dritten Quadranten) zum Graphen der Exponentialfunktion, da es sich um reziproke oder inverse Funktionen voneinander handelt.
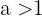
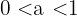
Mit KI zusammenfassen:













